
문제는 간단하지만 sum(arr[i:j+1])으로 풀면 시간초과가 난다. 이때 사용해야하는 알고리즘이 '누적합'이다.
누적합
누적합은 말 그대로 배열 원소들을 순서대로 누적시킨 합이다. 배열이 [1,2,3,4,5]일때, 누적합 배열은 [1, 1+2, 1+2+3, 1+2+3+4, 1+2+3+4+5], 즉 [1,3,6,10,15]가 된다.
i번째부터 j번째의 합을 구하고 싶다면, (j까지의 합) - (i-1까지의 합) 으로 나타낼 수 있다. 즉, i가 1일때는 arr[j-1] 자체가 답이 되고, i가 1보다 클때는 arr[j-1] - arr[i-2]가 답이 된다.
arr[j-1] = n[0] + n[1] + n[i-2] + n[i-1] + ... + n[j-1]
arr[i-2] = n[0] + n[1] + n[i-2]
# ------------------------------------------------------
arr[j-1] - arr[i-2] = n[i-1] + ... + n[j-1]시간복잡도
누적합을 사용하면 합을 미리 계산해두기 때문에 시간복잡도가 확 줄어든다.
0부터 N까지의 수 중에서 a번째부터 b번째까지의 구간합을 M번 구한다고 할때, 누적합을 사용하지 않으면 시간복잡도는 각각의 계산에서 O(N), 이 과정이 M번 반복되므로 O(NM)이다. 반면에 누적합을 사용하면 누적합을 계산하는데 O(N), 구간합을 계산하는데 O(1)이므로, 이 과정이 M번 반복되어도 시간복잡도는 O(N+M)이다.
코드
N, M = map(int, input().split())
numbers = list(map(int, input().split()))
s = 0
s_list = []
for n in numbers:
s += n
s_list.append(s)
for _ in range(M):
a, b = map(int, input().split())
if a == 1:
print(s_list[b-1])
else:
print(s_list[b-1]-s_list[a-2])2차원 배열에서의 누적합
➕ 2023-08-10 추가
백준 class 4를 풀다가 심화 문제가 있길래 정리
1. 누적합 계산하기
1차원배열일 때와 마찬가지로 다음과 같이 누적합 배열을 만든다.
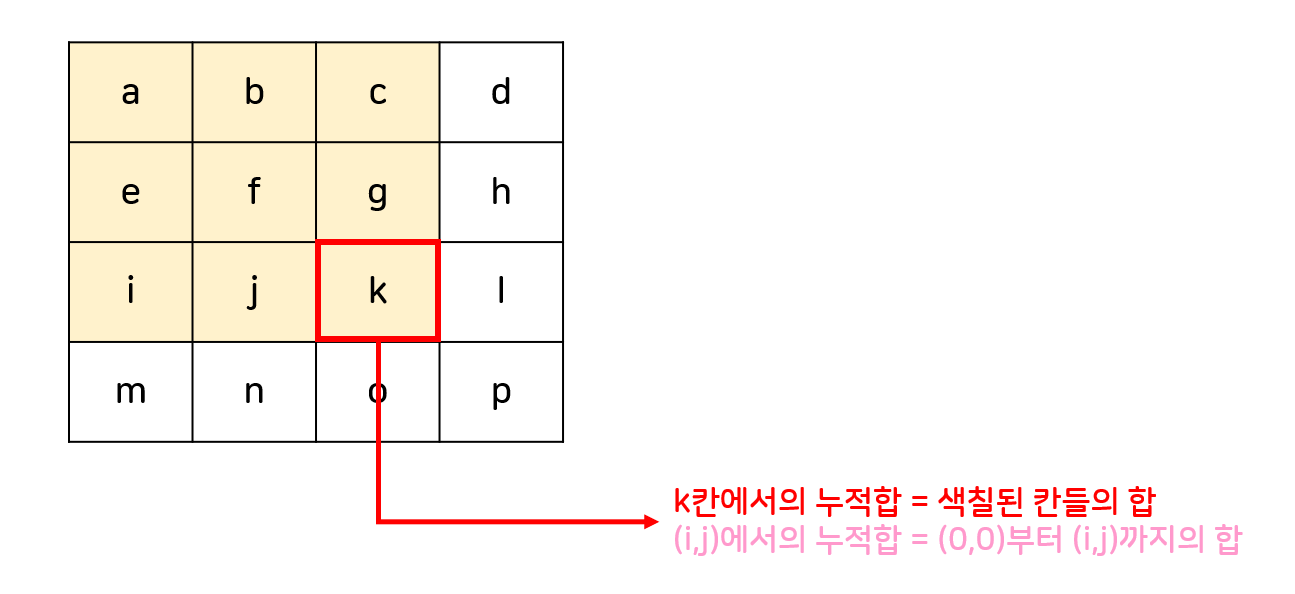
2. (x1, y1)부터 (x2, y2)까지의 합을 구하려면?

3. 코드
N, M = map(int, input().split())
board = []
for _ in range(N):
row = list(map(int, input().split()))
board.append(row)
s_list = [[0 for _ in range(N)] for _ in range(N)]
for i, row in enumerate(board):
s = 0
for j, r in enumerate(row):
s += r
if i == 0:
s_list[i][j] = s
else:
s_list[i][j] = s + s_list[i-1][j]
for _ in range(M):
x1, y1, x2, y2 = map(lambda x:int(x)-1, input().split())
answer = s_list[x2][y2]
if x1-1 >= 0:
answer -= s_list[x1-1][y2]
if y1-1 >= 0:
answer -= s_list[x2][y1-1]
if x1-1 >= 0 and y1-1 >= 0:
answer += s_list[x1-1][y1-1]
print(answer)cf) 누적합을 구할때 이렇게 구해도 된다.
s_list = [[0 for _ in range(N)] for _ in range(N)]
for i, row in enumerate(board):
for j, r in enumerate(row):
s_list[i][j] = board[i][j] + s_list[i][j-1] + s_list[i-1][j] - s_list[i-1][j-1]