

똑같은 문제인데 난이도에 따라 조건이 다르다.
- 실버2 - 길이만 구하면 됨 & N이 최대 1,000
- 골드2 - 길이만 구하면 됨 & N이 최대 1,000,000
- 플레5 - 길이랑 실제수열 둘 다 구해야함 & N이 최대 1,000,000
무작정 풀기보다 알고리즘 공부를 먼저 하고 푸는게 도움이 될 것 같아서 공부부터!
1. LIS(최장 증가 부분 수열)이란?

- LIS(Longest Increasing Subsequence)
- 어떠한 수열에서 오름차순으로 증가하는 가장 긴 부분 수열
- 이 때, 부분 수열의 각 수가 서로 연속할 필요는 없다.
- LIS는 여러개 존재할 수 있다.
LIS를 구하는 방법은 2가지다.
- DP
- 시간복잡도 : O(N^2)
- 최장길이와 실제 LIS 수열을 모두 구할 수 있다.
- 이분탐색
- 시간복잡도 : O(NlogN)
- 해당 방식으로는 최장 길이만 구할 수 있다. 실제 LIS 수열을 구하기 위해서는 역추적 과정을 거쳐야한다.
2. DP로 LIS 구하기
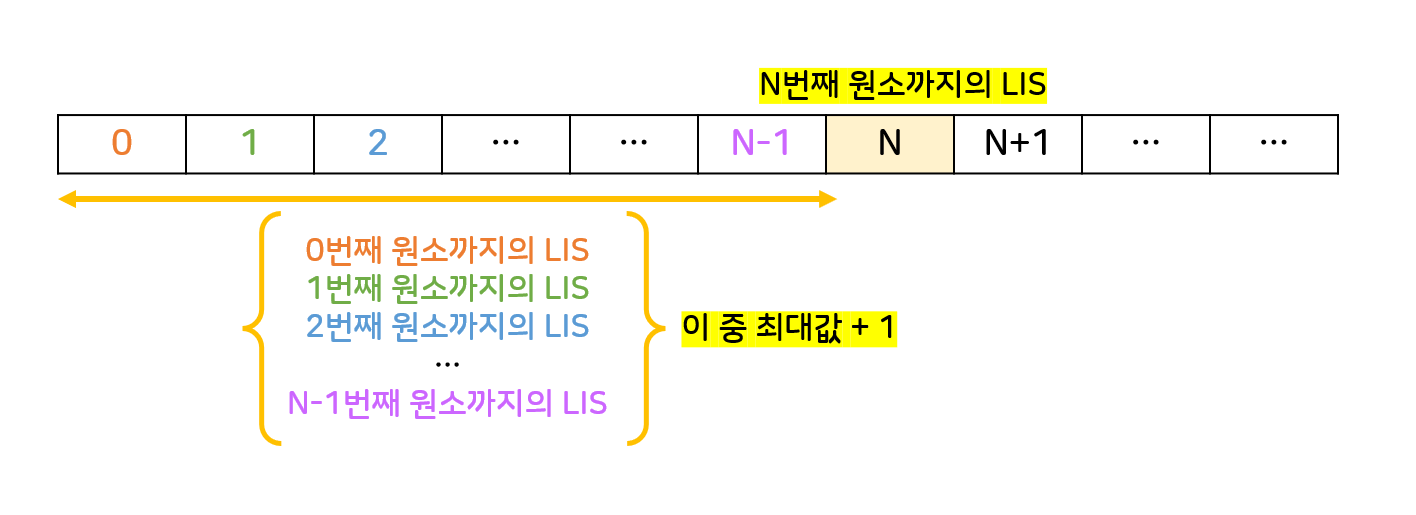
💡 N번째 수에서 끝나는 수열의 LIS = N번째 수의 앞에 있는 모든 원소 중 N번째수보다 작은 수에 대해 해당 원소에서 끝나는 LIS들 중 가장 긴 길이 + 1 💡
N번째 수에서 끝나는 수열의 LIS의 초기값은 기본적으로 1(자기자신)이다.
N번째 수의 앞에 있지만 N번째 수보다 크거나 같다면 이는 LIS가 아니게 되므로 무시한다.
동작 예시
수열 = [1, 5, 4, 2, 3, 8]
(1) 1에서 끝나는 수열 [1]의 LIS의 길이
- LIS =
[1] - 길이 =
1
(2) 5에서 끝나는 수열 [1,5]의 LIS의 길이
- LIS =
[1,5] - 길이 = (1) + 1 =
2
(3) 4에서 끝나는 수열 [1,5,4]의 LIS의 길이
- LIS =
[1,4] - 길이 = (1) + 1 =
2 - cf) 5 > 4 이므로 (2)는 무시
(4) 2에서 끝나는 수열 [1,5,4,2]의 LIS의 길이
- LIS =
[1,2] - 길이 = (1) + 1 =
2 - cf) 5 > 2, 4 > 2 이므로 (2), (3)은 무시
(5) 3에서 끝나는 수열 [1,5,4,2,3]의 LIS의 길이
- LIS =
[1,2,3] - 길이 = (4) + 1 =
3 - cf1) 5 > 3, 4 > 3 이므로 (2), (3)은 무시
- cf2) (4) > (1) 이므로 (4) 선택
(6) 8에서 끝나는 수열 [1,5,4,2,3,8]의 LIS의 길이
- LIS =
[1,2,3,8] - 길이 = (5) + 1 =
4 - cf) (5) > (1), (2), (3), (4) 이므로 (5) 선택
따라서 수열 [1, 5, 4, 2, 3, 8]의 LIS는 [1,2,3,8]로, 길이는 4이다.
코드
dp[i] = i번째 인덱스에서 끝나는 LIS의 길이 (초기값=1)array = [1,5,4,2,3,8]
dp = [1 for _ in range(len(array))]
for i in range(1, len(array)):
for j in range(i): # array의 처음부터 i-1번째까지
if array[i] > array[j]: # 현재값이 클때만
dp[i] = max(dp[i], dp[j]+1) # 더 큰 값으로 갱신
print(max(dp)) # 4이 방법은 간단하지만, 시간복잡도가 O(N^2)라 문제에 따라 시간초과가 날 수도 있다.
3. 이분탐색으로 LIS 구하기
기존 수열에서 현재 원소를 임의의 배열로 넣을 때, LIS를 유지하기 위한 최적의 위치를 이분탐색을 사용해서 구한 다음, 이 임의의 배열의 길이가 최대 몇까지 갔는지를 구하는 방식이다.
동작예시
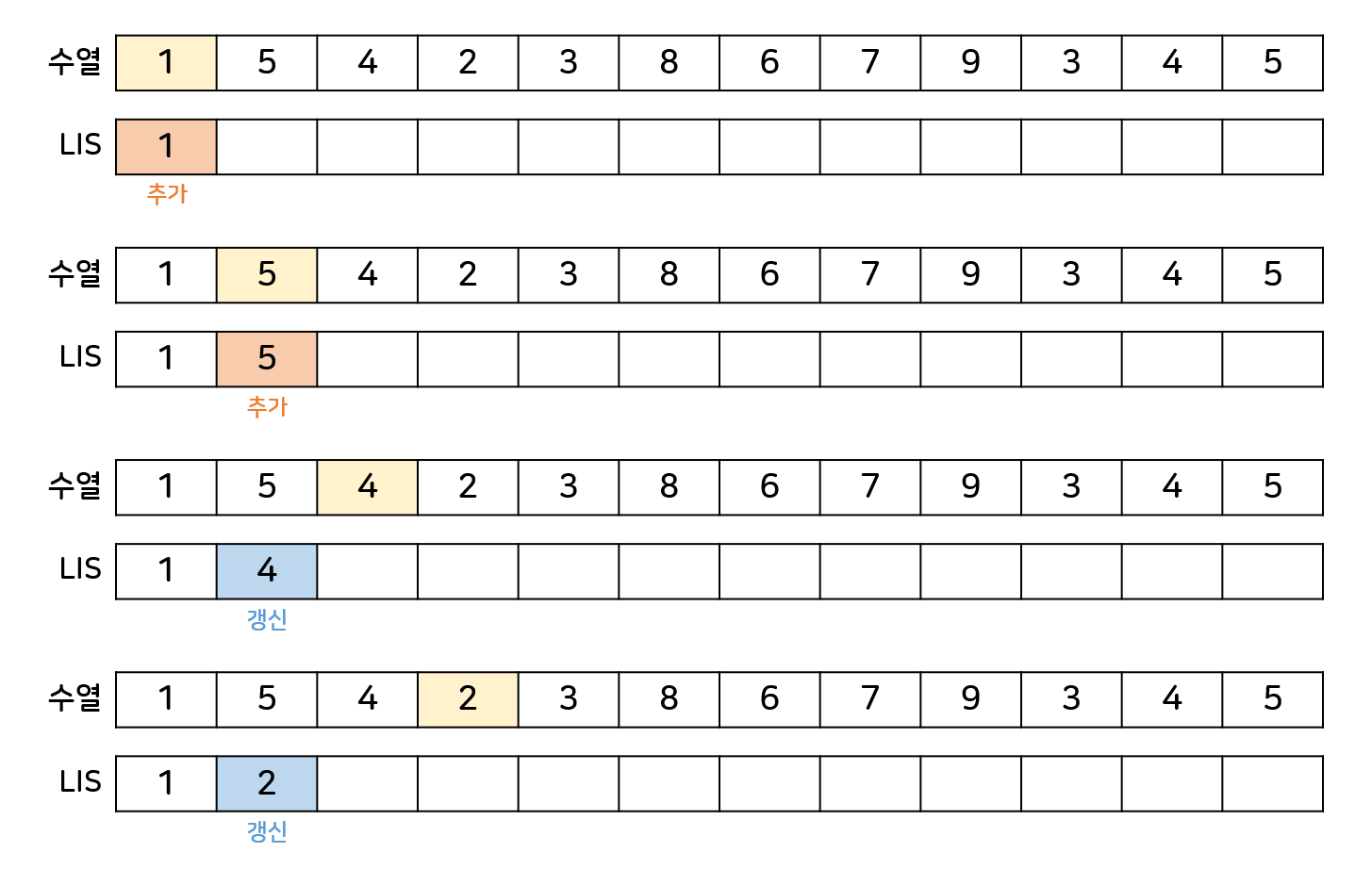
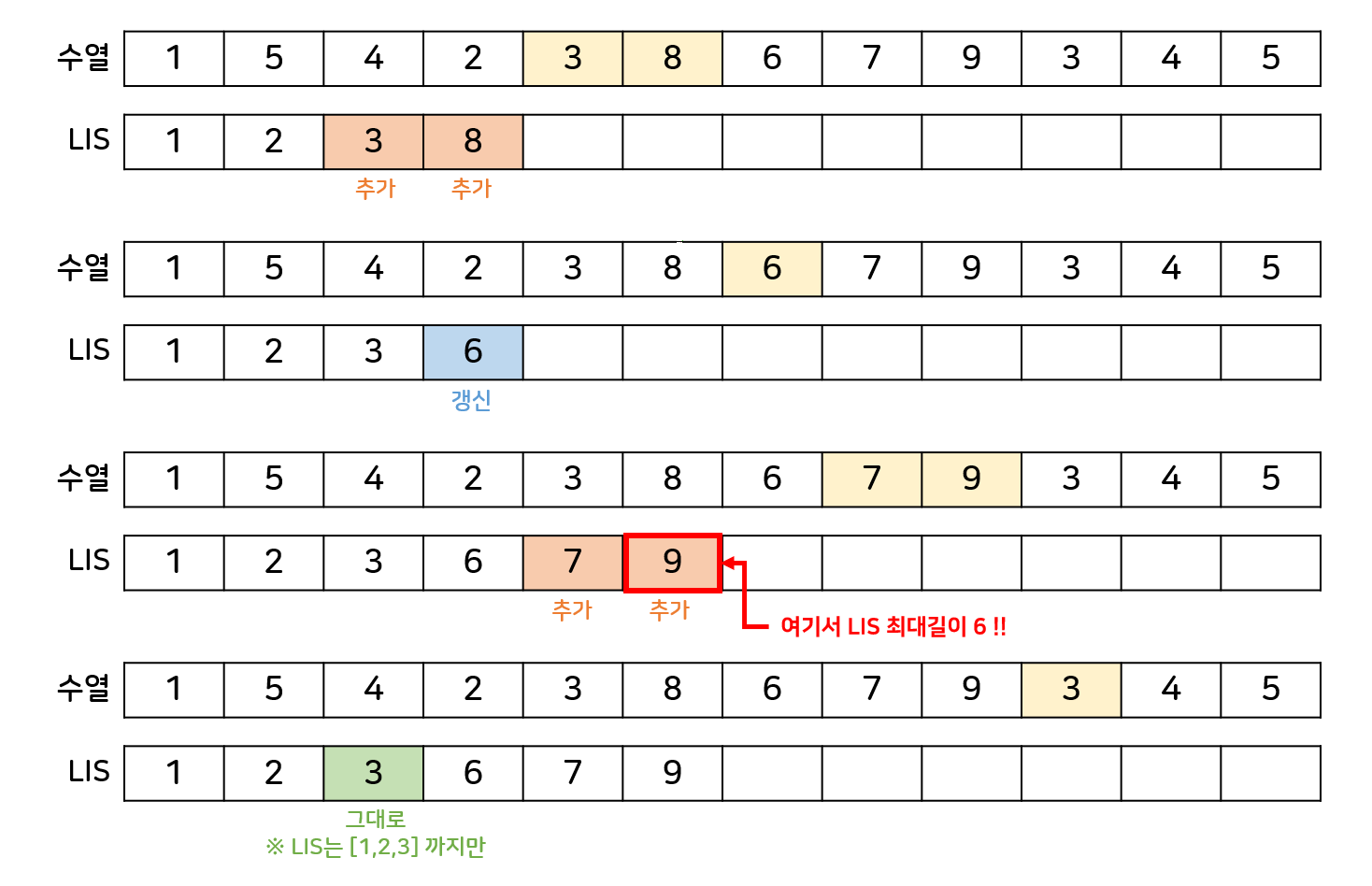
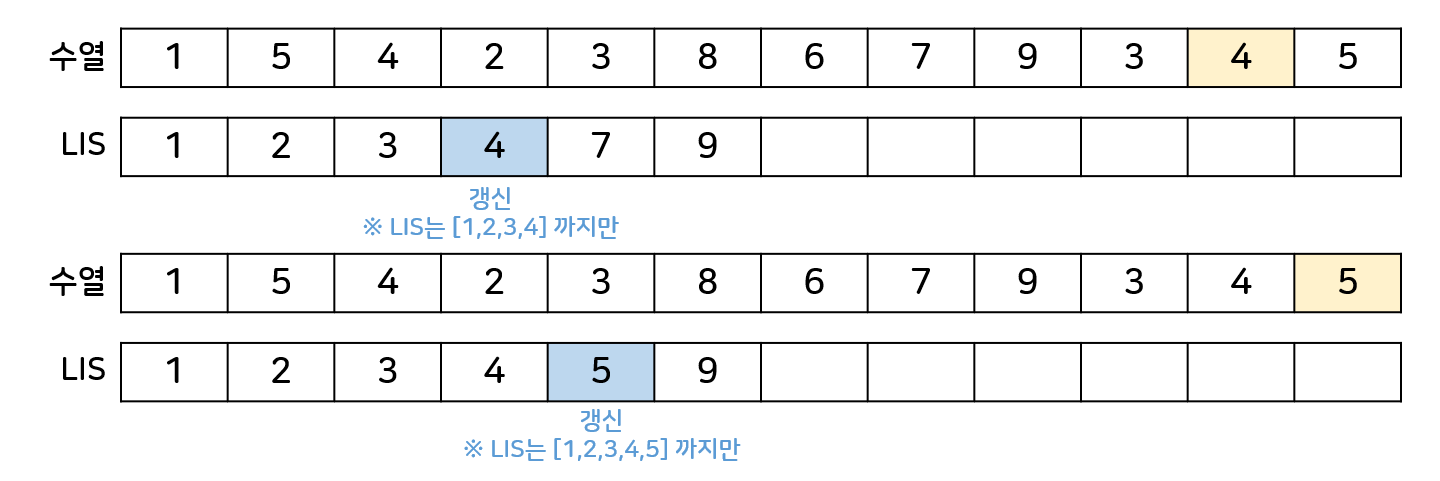
'수열'의 현재 원소가 'LIS'로 들어가기 위한 위치는 이분탐색으로 구하는 것이 중요 포인트!
위치를 찾고 해당 위치에 추가하거나 갱신한다.
LIS가 최대 얼마까지 길어졌는지가 답이다.
코드
from bisect import bisect_left
array = [1,5,4,2,3,8,6,7,9,3,4,5]
lis = [array[0]] # 첫번째 원소 넣고 시작
for i in range(len(array)):
if array[i] > lis[-1]: # lis의 마지막값보다 크다면 추가
lis.append(array[i])
else: # 그렇지 않다면 이분탐색으로 적절한 위치 찾기
idx = bisect_left(lis, array[i])
lis[idx] = array[i] # 갱신
print(len(lis)) # 6bisect 라이브러리를 써서 간단하게 작성할 수 있다.
⛳ 역추적으로 실제 LIS 구하기
(1) 참고
[Python] 백준 14003 - 가장 긴 증가하는 부분 수열 5
(2) 알고리즘
dp[i] = 주어진 수열의 i번째 값이 이분탐색 과정 중에 몇번째 인덱스에 들어갔는지 저장- 이분탐색을 하면서
dp배열에 해당값이LIS의 몇번째 인덱스에 들어갔는지 저장한다.
=>dp[i] = (LIS에서의 인덱스, 수열의 i번째 값) len(LIS)-1이lastIdx이고, 1씩 줄여가며 끝부터 거꾸로 값을 찾을 것이다.dp배열도N-1부터0까지 거꾸로 돈다.dp[i][0] == lastIdx이면dp[i][1]을 정답에 추가하고,lastIdx를 1 줄인다.- 추가한 정답들을 거꾸로 출력하면 실제 LIS가 나온다.
(3) 코드
from bisect import bisect_left
N = int(input())
numbers = list(map(int, input().split()))
lis = [numbers[0]]
dp = [(0,numbers[0])]
# 이분탐색으로 LIS 길이 구하기
for i in range(1,N):
if numbers[i] > lis[-1]:
lis.append(numbers[i])
dp.append((len(lis)-1, numbers[i]))
else:
idx = bisect_left(lis, numbers[i])
lis[idx] = numbers[i]
dp.append((idx, numbers[i]))
# 역추적으로 실제 LIS 구하기
L = len(lis)
lastIdx = L - 1
answer = []
for i in range(N-1,-1,-1):
if dp[i][0] == lastIdx:
answer.append(dp[i][1])
lastIdx -= 1
print(L) # LIS 길이
for a in answer[::-1]:
print(a, end=' ') # 실제 LIS 수열 (거꾸로 출력)
print()
잘 봤습니다! 혹시 이미지 출처를 밝히고 사용해도 될까요?!