
분할정복 (Divide and Conquer)
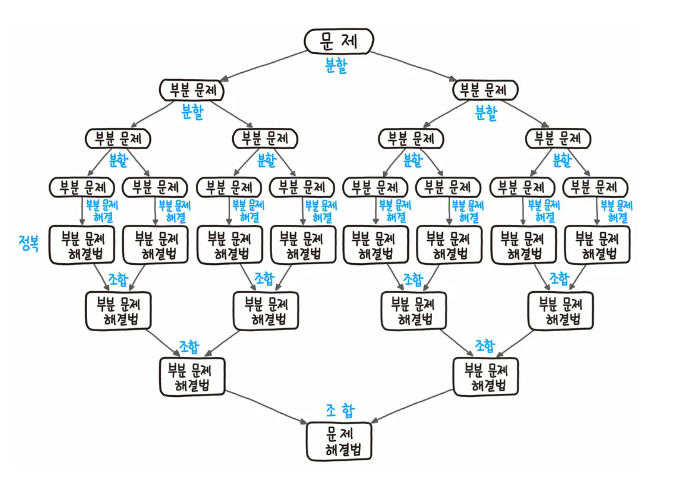
분할정복은 말 그대로 상단에서 분할(divide)하고, 중앙에서 정복(conquer)하고, 하단에서 조합(combine)하는 알고리즘이다.
- 분할(divide) : 문제를 더이상 분할할 수 없을 때까지 동일한 유형의 여러 하위 문제로 나눈다.
- 정복(conquer) : 가장 작은 단위의 하위 문제를 해결하여 정복한다.
- 조합(combine) : 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합한다.
분할정복을 사용하는 대표적인 예시로는 퀵소트와 합병정렬이 있다.
적용방식
def F(x):
if F(x)가 간단:
return F(x)를 계산한 값
else:
x를 x1, x2로 분할
F(x1)과 F(x2)를 호출
return F(x1), F(x2)로 F(x)를 구한 값[1629] 곱셈
이 문제는 '분할정복을 이용한 거듭제곱' 문제다.
근데 알고리즘을 알기 이전에 수학적인 사전 지식이 있어야 풀 수 있다.
# 지수 법칙
b가 짝수일때 : a^b = a^(b//2) * a^(b//2)
b가 홀수일때 : a^b = a^(b//2) * a^(b//2) * a
# 나머지 분배 법칙
(a + b) % c = ((a % c) + (b % c)) % c
(a * b) % c = ((a % c) * (b % c)) % ca^b를 지수법칙에 의해 쪼개고 쪼개서 b=1, 즉 a^1=a가 될때까지 쪼개고, 이때 c와 나눈 나머지를 계산한다. (b가 짝수일때와 홀수일때 쪼개지는 방식이 다르므로 경우의 수를 나누어서 쪼갠다.)
def DaC(a, b, c):
if b == 1:
return a % c
tmp = DaC(a, b//2, c)
if b % 2 == 0:
return (tmp * tmp) % c
else:
return (tmp * tmp * (a % c)) % c
A, B, C = map(int, input().split())
print(DaC(A, B, C))솔직히 아예 모르겠어서 답을 아예 찾아서 풀었는데 이 풀이를 도대체 어떻게 생각해내는건지 모르겠다. 자신감 뚝떨
[11444] 피보나치 수 6
평범한 피보나치 수를 구하는 문젠데 제한사항에 n의 최대범위가 1,000,000,000,000,000,000이다. (꼭 이렇게까지 과해야 돼..? ㅡㅡ)
처음엔 dp로 하려고 했는데 시간초과 때문에 감이 안와서 보니 얘도 문제 카테고리가 '분할정복을 이용한 거듭제곱'이었다.
도대체 어딜 봐서 얘가 거듭제곱인데..??
하고 찾아봤더니 피보나치를 행렬...로 바꿔야 한다고 한다. (ㅎ이걸 어케알아 내가)
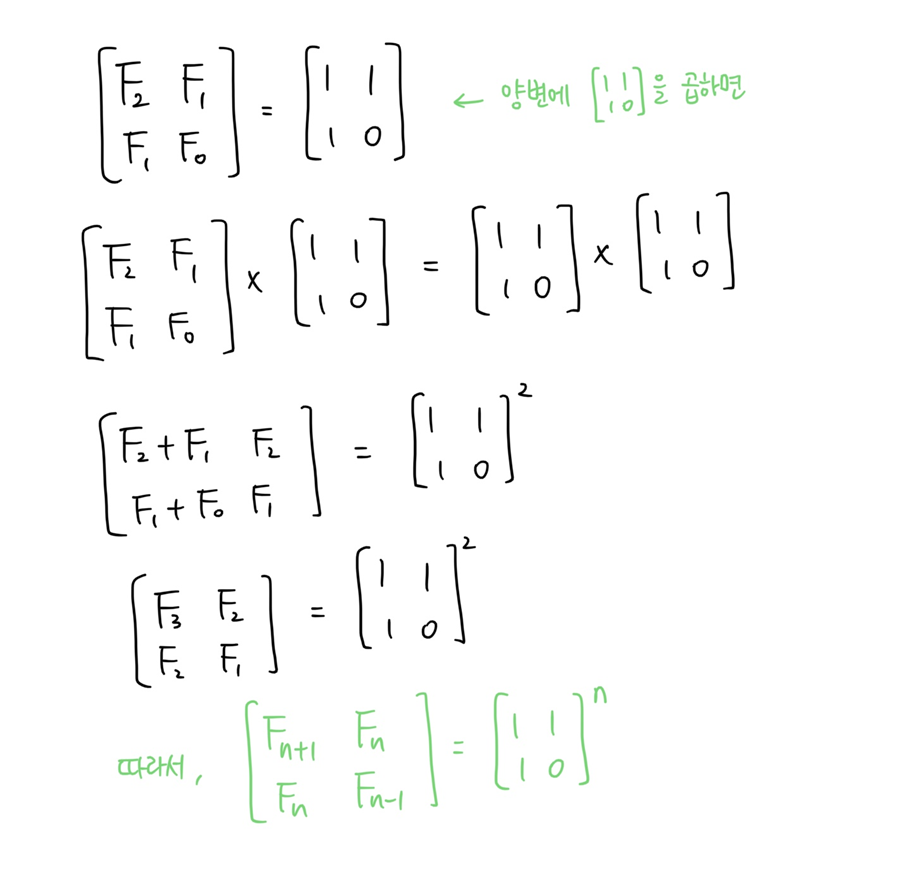
아하... 거듭제곱이 이래서 나왔구나
편의상 [(1,1), (1,0)]을 A라고 하자.
분할정복 기본코드와 위의 곱셈 문제에서 알게된 것을 토대로 의사코드를 작성하면 이렇다.
def DaC(n, A):
if n이 간단:
return A
tmp = DaC(n//2, A)
if n이 짝수:
return tmp X tmp # X는 행렬의 곱셈을 의미
else n이 홀수:
return tmp X tmp X A
# DaC(n, A) 반환값의 0행1열(or 1행0열)그래서 처음엔 이렇게 짰는데 시간초과가 났다. (어디 올리기 약간 부끄러운 행렬의 곱셈 하드코딩..ㅎ)
def DaC(n, A):
if n == 1:
return A
tmp = DaC(n//2, A)
a1 = tmp[0][0]*tmp[0][0] + tmp[0][1]*tmp[1][0]
a2 = tmp[0][0]*tmp[0][1] + tmp[0][1]*tmp[1][1]
a3 = tmp[1][0]*tmp[0][0] + tmp[1][1]*tmp[1][0]
a4 = tmp[1][0]*tmp[0][1] + tmp[1][1]*tmp[1][1]
if n % 2 == 0:
return [[a1,a2],[a3,a4]]
else:
return [[a1+a2,a1],[a3+a4,a3]]
n = int(input())
A = [[1,1],[1,0]]
print(DaC(n, A)[0][1]%1000000007)왜지?? 시간초과가 날 일이 뭐가있지?? 싶어서 다른사람들 코드를 찾아봤더니 대부분 행렬의 곱셈을 함수로 따로 빼서 계산하고 있었고, 내 코드에서 시간초과가 난 이유는 아마 계산 중에 나머지 연산(%1000000007)을 안하고 마지막에만 해서 그런거 같았다.
그래서 이렇게 고쳤다.
def DaC(n, A):
if n == 1:
return A
tmp = DaC(n//2, A)
if n % 2 == 0:
return matrix_multiple(tmp, tmp)
else:
return matrix_multiple(matrix_multiple(tmp, tmp), A)
def matrix_multiple(A, B):
result = []
for i in range(2):
tmp = []
for j in range(2):
s = 0
for k in range(2):
s += A[i][k] * B[k][j]
tmp.append(s%1000000007)
result.append(tmp)
return result
n = int(input())
A = [[1,1],[1,0]]
print(DaC(n, A)[0][1]%1000000007)그랬더니 통과함.
💡 "수가 너무 커지니까 얼마로 나눈 나머지를 출력하세요!"라고 명시된 문제에는 이걸 결과값에만 적용할게 아니라 중간 계산값에도 넣어야 하는 거 같다. 나름 중요한 포인트?
➕ 행렬의 곱셈
행렬의 곱셈 인덱스 다루는게 겁나 헷갈려서 이참에 외워버리는게 낫겠다 싶었다.
M = [[0 for _ in range(len(B[0]))] for _ in range(len(A))]
for i in range(len(A)):
for j in range(len(B[0])):
for k in range(len(A[0])):
M[i][j] += A[i][k] * B[k][j]두 문제 정도 풀어보니까 어떤 식으로 풀어야하는지 감은 오는거 같은데 그냥 문제 특성상? 풀이 흐름을 뭔가 확실하게 나타내기가 좀 애매한거 같다.
