

이 문제를 요약하자면
"그래프의 모든 정점을 딱 한번씩만 지나면서 시작점과 끝점이 같은 경로를 찾아라"
이다.
해밀턴 순환
-
해밀턴 경로 : 그래프의 모든 정점을 딱 한번씩만 지나는 경로
-
해밀턴 순환 : 시작점과 끝점이 똑같은 해밀턴 경로
= 그래프의 모든 정점을 딱 한번씩만 지나면서 시작점과 끝점이 같은 경로
TSP (Traveling Salesman Problem)
두둥. 외판원 순회 문제의 다른 이름 TSP (유명하다고 한다.)
TSP는 비용이 최소가 되는 해밀턴 순환을 찾는 문제다.
시작점?
💡 특이한 점은 이를 구하기 위해 시작점을 특정할 필요가 없다는 것이다.
어차피 순환 하나를 찾으면 해당 순환에서 모든 시작점~끝점이 나오기 때문에 임의의 점 하나에서만 탐색을 하면 된다.
ex) 1->2->3->4->1 == 2->3->4->1->2 == 3->4->1->2->3 == ...
사용할 수 있는 알고리즘
- n≤11 일 때 : 완전탐색
- n≤12 일 때 : 백트래킹
- n≤16 일 때 : 비트필드를 이용한 DP

문제에 대놓고 비트필드를 이용한 DP로 풀라고 나와있었다.
이 문제를 풀려면 비트마스킹, DP, DFS.. 3가지나 사용해야 한다.
- 도시 방문 여부 저장 = 비트마스킹
- 현재 도시에서의 최소비용 저장 = DP
- 도시를 방문하는 순서 = DFS
1. 비트마스킹
- 비트마스킹으로 방문한 도시 나타내기
4 3 2 1
0 0 0 0 => 0 (visited 최솟값)
0 0 0 1 => 1 (1번도시 방문함)
...
1 0 1 0 => 10 (2번도시와 4번도시 방문함)
...
1 1 1 1 => 15 (visited 최댓값)- 방문한 도시 추가하기
visited | (1 << next) # next = 추가할 도시- 해당 도시를 방문했는지 확인하기
visited & (1 << next) # next = 확인할 도시- 모든 도시에 방문했는지 확인하기
visited == (1 << N) - 1 # N = 도시의 수2. DP
- DP가 의미하는 것
dp[현재도시][지금까지 지난 도시(비트마스킹)] = 현재도시에서 남은 도시들을 거쳐 다시 출발점으로 돌아오는 비용
dp[cur][visited] = 현재 cur도시이며 방문현황은 visited이고, 아직 방문하지 않은 도시들을 모두 거쳐 다시 시작점으로 돌아가는데 드는 최소 비용- 점화식
dp[cur][visited] = min(dp[cur][visited], dp[next][visited | (1 << next)] + W[cur][next])이해가 잘 안가니 예시를 보자.
- 예시
현재 0번도시이고, 2번도시와 3번도시에 각각 갈 수 있는 상황
1) 2번도시 방문
dp[0][0011] = dp[2][0111] + W[0][2]
현재 0번도시이고, 0,1번도시를 방문하였으며, 2,3번도시를 방문한 후 다시 시작점으로 돌아갈 때의 최소비용 = 현재 2번도시이고, 0,1,2번도시를 방문하였으며, 3번도시를 방문한 후 다시 시작점으로 돌아갈 때의 최소비용 + 0번도시에서 2번도시로 이동하는 비용
2) 3번도시 방문
dp[0][0011] = dp[3][1011] + W[0][3]
현재 0번도시이고, 0,1번도시를 방문하였으며, 2,3번도시를 방문한 후 다시 시작점으로 돌아갈 때의 최소비용 = 현재 3번도시이고, 0,1,3번도시를 방문하였으며, 2번도시를 방문한 후 다시 시작점으로 돌아갈 때의 최소비용 + 0번도시에서 3번도시로 이동하는 비용
3) 1)과 2)에서 구한 값 중 더 작은값이 최종적으로 dp[0][0011]이 된다.
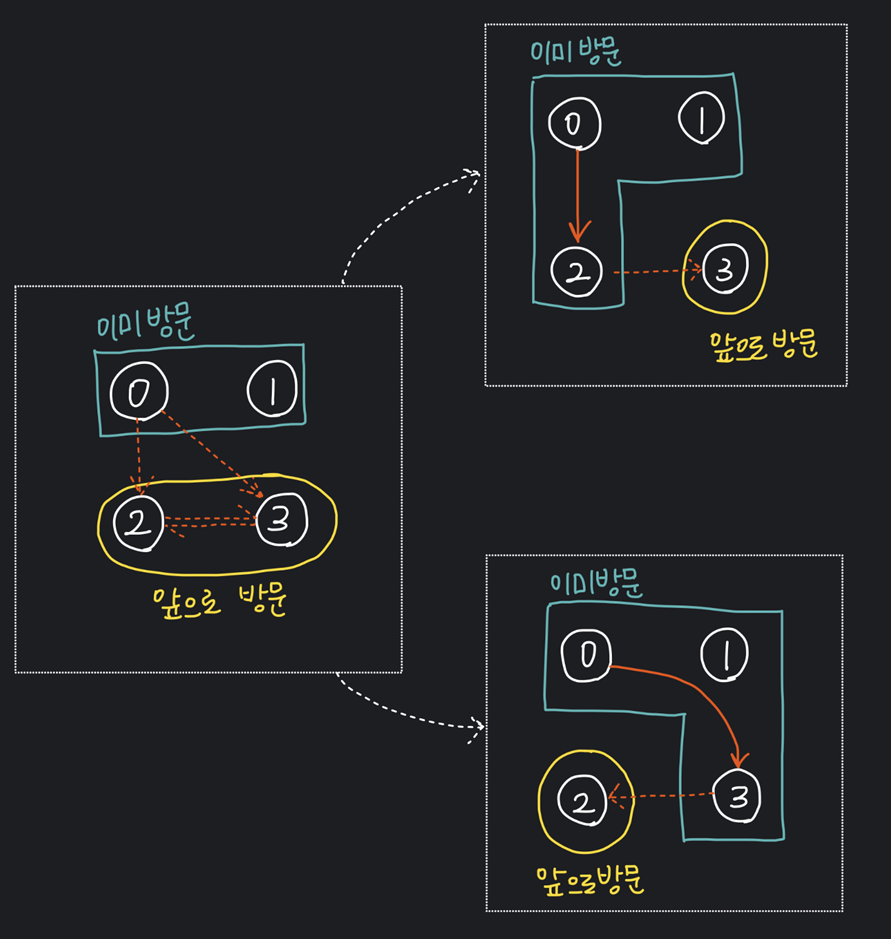
그림으로 그려보니 '앞으로 방문해야하는 도시들'을 작게 쪼갠 다음 그 결과를 사용해 연산을 하기 때문에 DP인거같다.
- 내가 지금 0이고 앞으로 방문해야할 도시 = 1,2,3 이라면,
- 0에서 1을 방문하면 앞으로 방문해야할 도시 = 2,3 이 되고,
- 1에서 2를 방문하면 앞으로 방문해야할 도시 = 3 이 됨
그런데 그동안 푼 DP들처럼 DP배열을 차곡차곡 쌓는게 아니라 DFS 탐색 순서에 따라 왔다리갔다리하면서 채워서 더 어려웠던 것 같다.
- 재귀
코드를 쓸 때는 dp[next][visited | (1 << next)]를 dfs(next, visited | (1 << next))으로 써서 재귀함수로 dp를 계속 갱신해야 한다.
3. DFS
DFS로 탐색하는 부분만 나타내면 아래와 같다.
def dfs(현재도시, 현재까지방문한도시):
if 모든 도시를 방문했거나 이미 계산한 값일 때:
return
else:
for 다음도시 in 존재하는모든도시들:
if 현재도시->다음도시로 갈 수 있을 때:
dp[현재도시][현재까지방문한도시] = dfs(다음도시,현재까지현재방문한도시+다음도시)
+ (현재도시->다음도시 가중치) 中 최솟값
return dp[현재도시][현재까지방문한도시]최종코드
import sys
input = sys.stdin.readline
def dfs(cur, visited):
if visited == (1 << N) - 1: # 모든 도시를 다 방문했으면
if W[cur][0] != 0: # 현재(마지막)도시에서 원점으로 돌아갈 수 있을 때
return W[cur][0] # 현재(마지막)도시에서 원점으로 돌아가는 간선의 가중치
else: # 원점으로 돌아갈 수 없을 때
return INF # 불가능, 무한대 반환
if dp[cur][visited]: # 이미 계산한 부분일 때
return dp[cur][visited] # 해당값 반환
left = INF
for next in range(1, N): # 시작점0 이후로 존재하는 모든 도시들
if W[cur][next] == 0: # 현재도시->다음도시로 가는 간선이 없을 때 pass
continue
if visited & (1 << next): # 다음도시가 이미 방문한 도시일 때 pass
continue
# 정상적으로 다음도시로 갈 수 있을 때 => 점화식 계산(위 설명 참고)
left = min(left, dfs(next,visited|(1<<next)) + W[cur][next])
dp[cur][visited] = left # 최종적으로 구한 최소값 넣기
return dp[cur][visited]
N = int(input())
W = []
INF = 1e9
dp = [[0 for _ in range(1<<N)] for _ in range(N)] # 0으로 초기화해야함
for _ in range(N):
W.append(list(map(int, input().split())))
print(dfs(0, 1)) # 시작점은 0, 0번도시만 방문한 상황(00....001)주의할 점은 dp를 INF로 초기화하면 시간초과가 난다. 0으로 초기화해야한다.
그렇다고 한다..
솔직히 다음에도 나오면 못풀듯
