
📌 그래프는 자료구조편과 알고리즘편, 알고리즘-최단경로편, 코드편 총 4편으로 나누어서 작성
📌 "엣지를 지나 그래프의 노드를 탐험해봅시다."
출제빈도 : 낮음
평균점수 : 낮음
코드
1. 가장 먼 노드 (Lv. 3)
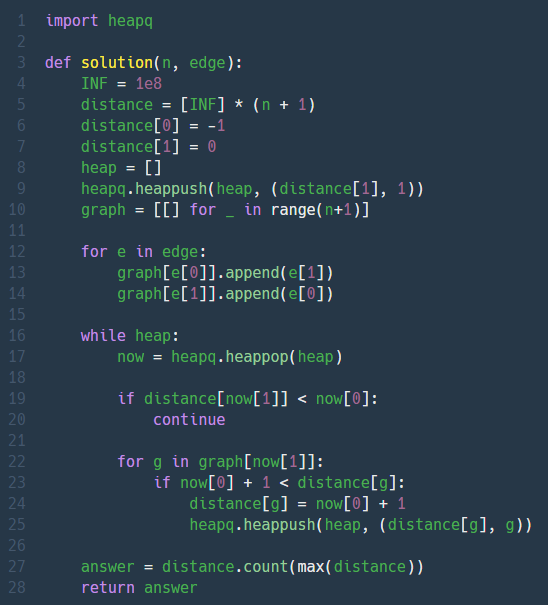
다익스트라 알고리즘을 사용해서 최단거리 테이블의 최대값이 몇개인지 세면 끝. 문제에서 가중치는 따로 주어지지 않아서 모든 간선이 가중치 1을 가지는 것으로 계산했다.
잠시 삐끗했던 부분은 새로운 노드를 힙에 언제 삽입하느냐? 와 처음 공부할때도 무슨 역할이었는지 싶었던 19~20번째줄! (다시 정리해둠)
- 거리 계산은
현재노드까지의 최단거리 + 현재노드에서 다음노드로 가는 거리vs이전에 계산해둔 다음노드로 가는 최단거리를 비교하는 것 - 이번에 계산한 값이 기존값보다 작아서 최단경로 테이블을 갱신할때 힙에도 삽입한다. (값이 바뀌었으니 이후 경로 계산에 반영해야하니까 당연한 것! 힙에 삽입하는 순서와 값을 빼서 사용하는 순서는 다르다!!)
이전에 계산해둔 현재노드까지의 최단거리가지금부터 볼 현재노드까지의 최단거리보다 작다면 볼 필요가 없으므로 이후 과정 생략 (이부분이 없으면 무한루프로 빠진다.)
2. 순위 (Lv. 3)
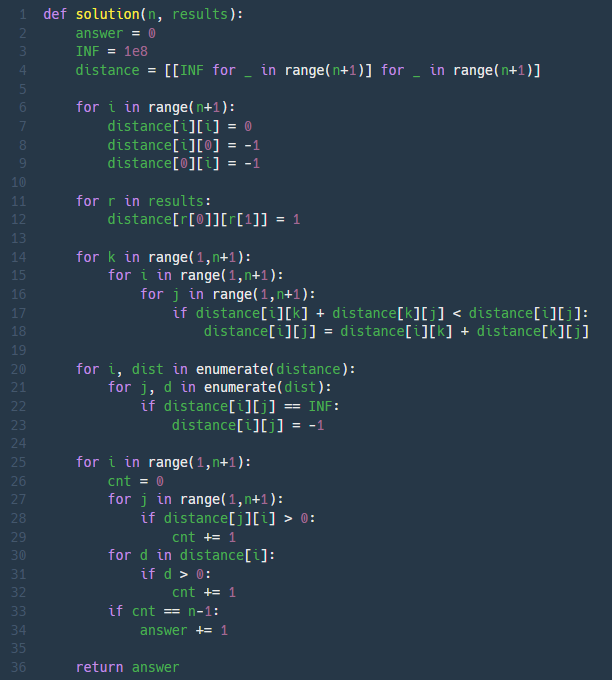
문제에서 주어진 [이긴 선수, 진 선수]를 그래프 상에서 이긴 선수 -> 진 선수로 표시하면 아래와 같이 그래프를 그릴 수 있다.
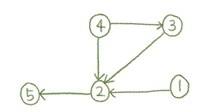
A 선수의 정확한 순위를 매기려면, 모든 선수에 대해 다른 선수에서 A 선수로 오거나(A 선수가 지는 경우), A 선수에서 다른 선수로 가는(A 선수가 이기는 경우) 경로가 모두 합해 전체선수의 수-1개가 있어야 한다. (정확한 등수를 따질 필요는 없으므로 전체 개수만 맞으면 된다.)

모든 선수쌍에 대해 가능한 경로를 모두 구해야하므로 플로이드 워셜 알고리즘을 사용했다. 그리고 경로가 존재하는 이기는 경우와 지는 경우를 합해서 전체선수의 수-1이면 답을 하나씩 증가시켰다.
(보류) 3. 방의 개수 (Lv. 5)
레벨5는 넘 어렵자낭
느낀점
- '그래프 알고리즘'이라고 검색하면 크루스칼 알고리즘이랑 위상정렬이 제일 먼저 나오길래 최단경로는 나중에 정리할까 하다가 그냥 하는 김에 한방에 정리했는데, 문제에서는 최단경로만 나왔다.
머쓱먼저 봐두길 잘한듯! - 다익스트라, 플로이드 워셜, 벨만 포드 중 문제에 적합한 알고리즘을 적절히 고르는 것이 중요하다. 사용할 알고리즘을 잘 고르고 나면 코드 구현 자체는 알고리즘의 정석 코드 틀 밖으로 잘 벗어나지 않는다. (아직은?)
🎉프로그래머스 고득점 Kit 완료!!🎉
(DFS/BFS 1문제랑 그래프 1문제 빼고 ㅎ)
첫 시작으로 코테 입문 레벨0 100문제 푸는데 이틀 (2023.06.25 ~ 2023. 06. 26)
레벨1 77문제 푸는데 일주일 (2023.06.28 ~ 2023.07.04)
고득점 키트 45문제 푸는데 20일 (2023.07.05 ~ 2023.07.24)
코테 공부 시작한지 딱 한달만에 고득점 키트까지 완료했다!! 🥳🥳
코테 공부라는 명목 하에 자료구조랑 알고리즘도 공부하면서 벨로그에 틈틈히 정리해뒀으니 나름.. CS 공부도 같이 했다쳐 (?)
학교 다닐때 나름 공부를 열심히 했었는지 대부분 대충 쓱 보고도 아 이거~ 하고 이해가 수월하게 돼서 다행이었다. 자료구조 ㅅㅈㅁ 교수님과 알고리즘 ㅇㅇㅅ 교수님 감사합니다.. (´▽`ʃ♡ƪ)
✏️ 앞으로 할 것 : 백준 solved.ac 클래스 문제 풀기
