
📌 "불필요한 계산을 줄이고, 효율적으로 최적해를 찾아야만 풀리는 문제들입니다."
출제빈도 : 낮음
평균점수 : 낮음
동적계획법(Dynamic Programming)이란?
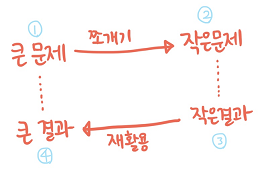
하나의 큰 문제를 여러개의 작은 문제로 나눠 그 결과를 저장한 다음 큰 문제를 해결할때 다시 사용하는 것
이미 계산한 것을 메모리에 저장하여 중복 계산을 막고, 수행 시간의 효율성을 향상시킨다.
알고리즘의 진행에 따라 탐색해야할 범위를 '동적'으로 결정한다.
DP를 적용하기 위한 조건
-
겹치는 부분 문제 (Overlapping Subproblems)
: 동일한 작은 문제들이 반복(중복)해서 나타나는 경우 -
최적 부분 구조 (Optimal Substructure)
: 작은 부분 문제의 최적 결과값을 사용해서 전체 문제의 최적 결과를 낼 수 있는 경우
DP의 접근방법
1. Bottom-Up (상향식)
- 반복문
- 아래(작은문제)에서 위(큰문제)로
- 크기가 작은 문제부터 풀면서, 점점 크기를 키워가며 저장해둔 작은 문제의 답을 활용해서 큰 문제를 푼다.
2. Top-Down (하향식)
- 재귀함수
- 위(큰문제)에서 아래(작은문제)로
- 크기가 큰 문제에서 작은 문제로 쪼개가며 재귀호출을 통해 문제를 푼다.
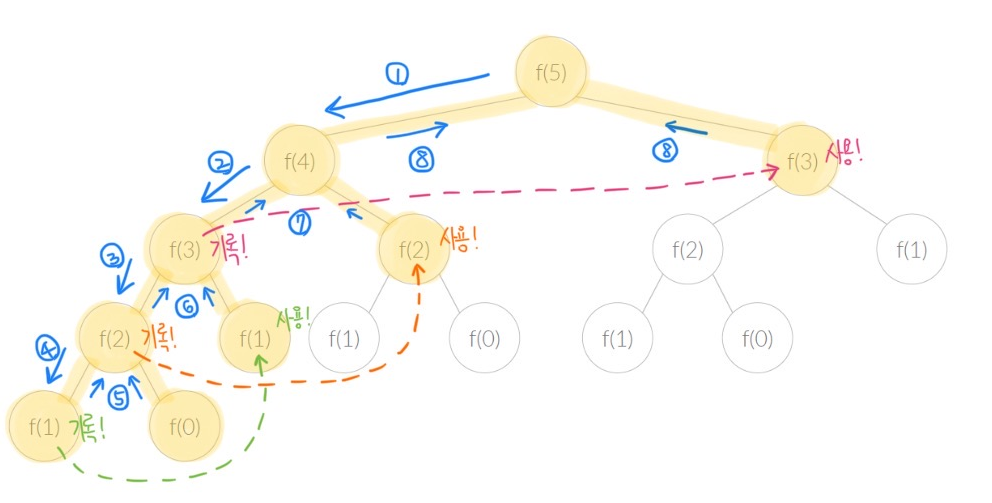
대표적인 예시 : 피보나치 수열
cf) 피보나치 수열 = 직전 두 항의 합이 다음 항이 되는 수열
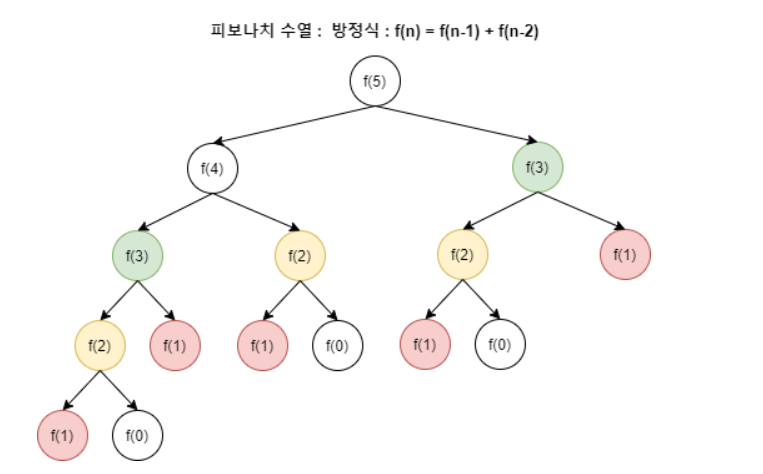
1. Bottom-Up
: 작은 문제부터 큰 문제로, 반복문
d = [0] * 100
d[1] = 1
d[2] = 1
n = 99
for i in range(3, n + 1):
d[i] = d[i - 1] + d[i - 2]
print(d[n])2. Top-Down
: 큰 문제부터 작은 문제로, 재귀호출
d = [0] * 100
def fibo(x):
if x == 1 or x == 2:
return 1
if d[x] != 0:
return d[x]
d[x] = fibo(x-1) + fibo(x-2)
return d[x]
print(fibo(99))코드
프로그래머스 고득점 Kit - 동적계획법(Dynamic Programming) 문제목록
1. N으로 표현 (Lv. 3)
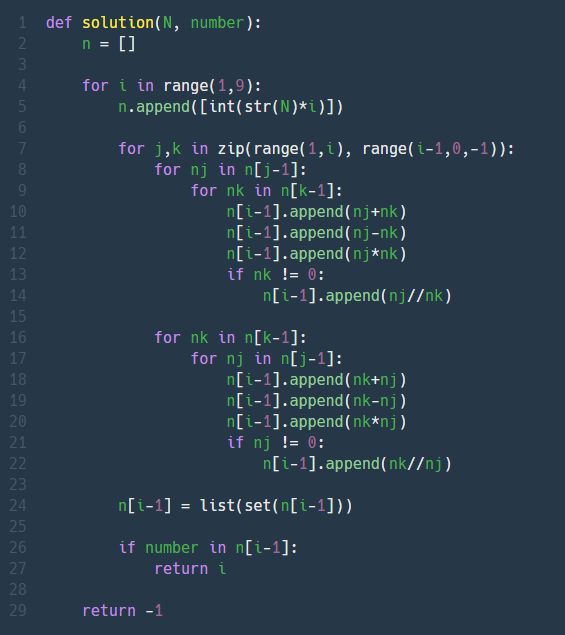
아이디어가 도저히 생각이 안나서 규칙만 찾아보고 풀었다. 결론적으로 저렇게 끔찍한 코드를 짜고도 시간초과가 안난게 용하다.
-
1단계
N을 1번 사용해서 만들 수 있는 수
= [N] -
2단계
N을 2번 사용해서 만들 수 있는 수
= [NN,N+N,N-N,N*N,N/N]
= [NN,
{N을 1번 사용해서 만들 수 있는 수} x {+,-,*,/} x {N을 1번 사용해서 만들 수 있는 수}] -
3단계
N을 3번 사용해서 만들 수 있는 수
= [NNN,N+(N+N),N-(N+N),N*(N+N),N/(N+N), ...]
= [NNN,
{N을 1번 사용해서 만들 수 있는 수} x {+,-,*,/} x {N을 2번 사용해서 만들 수 있는 수},
{N을 2번 사용해서 만들 수 있는 수} x {+,-,*,/} x {N을 1번 사용해서 만들 수 있는 수}] -
...
-
n단계
N을 n번 사용해서 만들 수 있는 수
= [NN..(n번)..N,
{N을 1번 사용해서 만들 수 있는 수} x {+,-,*,/} x {N을 n-1번 사용해서 만들 수 있는 수},
{N을 2번 사용해서 만들 수 있는 수} x {+,-,*,/} x {N을 n-2번 사용해서 만들 수 있는 수},
{N을 3번 사용해서 만들 수 있는 수} x {+,-,*,/} x {N을 n-3번 사용해서 만들 수 있는 수},
...
{N을 n-1번 사용해서 만들 수 있는 수} x {+,-,*,/} x {N을 1번 사용해서 만들 수 있는 수}]
문제의 최대값이 8이므로 n단계는 사실상 8단계가 끝이다.
현재 단계에서 구할 수 있는 계산결과를 찾기 위해 이전에 계산해둔 값들을 사용하기 때문에 DP문제라고 할 수 있다.
number를 시작으로 문제를 푸는게 아니라, 진짜 완전 바닥부터 시작하다가 number가 나오면 코드를 끝내는 방식으로 풀었다.
2. 정수 삼각형 (Lv. 3)

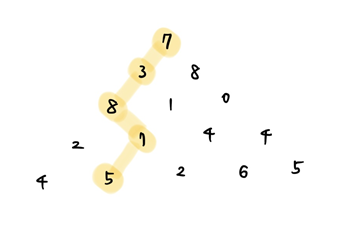
삼각형의 바닥부터 시작!
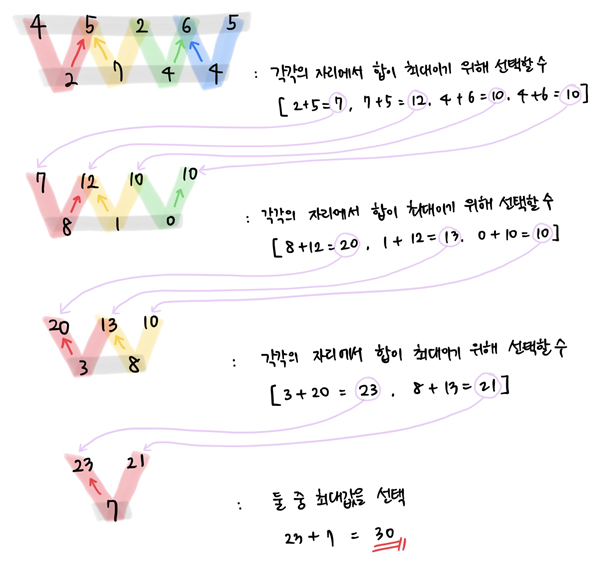
그럼 결론적으로 아래와 같은 경로로 지날때 합이 최대가 된다.
지나는 경로의 합의 최대를 구하기 위해서 가능한 경우의 수가 적은 가장 바닥부터 경로합을 구해가며 올라갔다.
문제에서 요구하는 큰 경로의 합을 구하기 위해 작은 경로로 쪼개서 작은 경로의 합을 재활용해 큰 경로의 합을 구했다는 점에서 DP이긴한데, 시간복잡도를 줄이기 위해 사용 가능한 작은 경로의 합들 중에 최대값만 사용했다는 점에서 그리디이기도 한 것 같다.
3. 사칙연산 (Lv. 4)
프로그래머스 > 찾아라 프로그래밍 마에스터 > 사칙연산
[프로그래머스] 사칙연산 - Java
🧱🧱🧱🧱(아직) 넘을 수 없는 레벨4의 벽🧱🧱🧱🧱
정말 많은 사람들의 풀이를 보고 겨우겨우 어거지로 따라쳐서 통과했다..😮💨 그냥 문제 푸는데 필요했던 핵심만 간단하게만 정리하면
# 사용할 자료구조
dp_max[i][j] = [i]~[j]번째 피연산자까지의 연산결과 중 최대값
dp_min[i][j] = [i]~[j]번째 피연산자까지의 연산결과 중 최소값
# i <= k < j
[i]~[j]까지의 연산결과 중 최대값 = 모든 [i][k]~[k+1][j] 결과 중 최대값
[i]~[j]까지의 연산결과 중 최소값 = 모든 [i][k]~[k+1][j] 결과 중 최소값
# 왼쪽 수식이 최대가 되려면
(a + b) => (max + max) # 1. (a + b)가 최대가 되는 경우
(a - b) => (max - min) # 2. (a - b)가 최대가 되는 경우
-(a + b) => -(min + min) # 3. (a + b)가 최소가 되는 경우
-(a - b) => -(min - max) # 4. (a - b)가 최소가 되는 경우
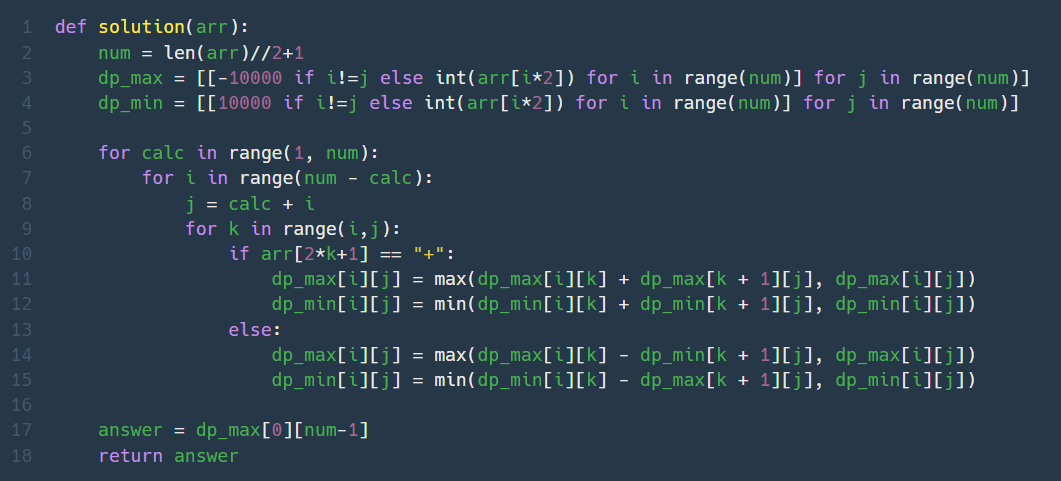
# 코드로 짜면
if "+": # (max + max), -(min + min)
dp_max[i][j] = max(dp_max[i][k] + dp_max[k + 1][j], dp_max[i][j]) # 1
dp_min[i][j] = min(dp_min[i][k] + dp_min[k + 1][j], dp_min[i][j]) # 3
else "-": # (max - min), -(min - max)
dp_max[i][j] = max(dp_max[i][k] - dp_min[k + 1][j], dp_max[i][j]) # 2
dp_min[i][j] = min(dp_min[i][k] - dp_max[k + 1][j], dp_min[i][j]) # 44. 등굣길 (Lv. 3)
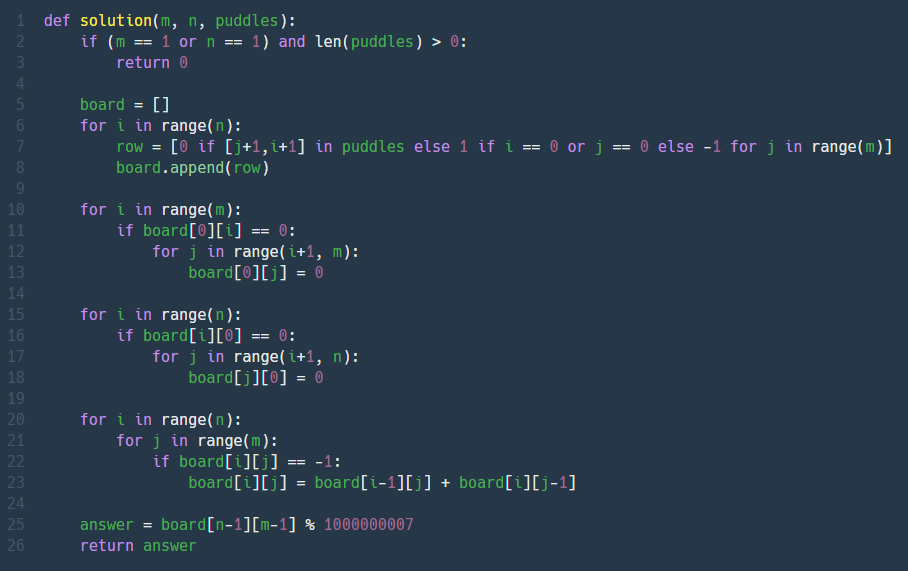
테케 몇개가 실패해서 보니까 기본판 생성 과정에서 예외케이스(맨윗줄, 맨왼쪽줄에 웅덩이가 있으면 해당 줄의 다음칸으로는 갈 수 없으니까 모두 0으로 변경해야함)를 발견해서 코드가 좀 구려졌는데.. 최적화하기 귀찮아서 안할거다.
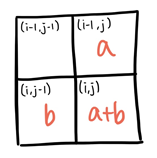
핵심아이디어 : (i,j)에 올 수 있는 최단경로의 수 = (i-1, j)에 올 수 있는 최단 경로의 수 + (i, j-1)에 올 수 있는 최단경로의 수
오른쪽과 아래쪽으로밖에 이동하지 못한다는 건, 모든 경로가 최단경로라는 뜻
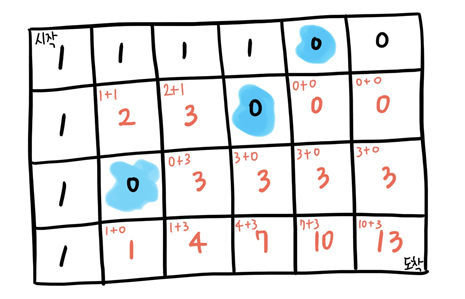
시작점(0,0)부터 시작해서 한칸씩, 이전 단계에서 계산해둔 내 윗칸과 왼쪽칸에 있는 수들을 더해서 칸들을 채우다가 도착지점(m,n)에 도달하면 종료한다.
5. 도둑질 (Lv. 4)
도저히 뭐 어쩌라는건지 모르겠어서 다른 사람 풀이를 보고 풀었다.
인접한 두 집은 털지 못하므로, 무조건 한 집 이상씩 건너 뛰어서 털어야 한다. 1번집과 마지막집은 인접해있으므로, 1번집을 털었으면 마지막집은 털지 못한다. 1번집을 털지 않았으면 마지막집까지 털어도 된다.
따라서 두 가지 경우로 나뉜다.
1번집 털기+2번집부터 마지막 바로 전 집까지 털기1번집 안털기+2번집부터 마지막 집까지 털기

n번집을 털때, 최대로 터는 돈의 액수를 dp[n]이라고 하면
case 1. n-1번집을 털었으면 n번집은 못터니까 dp[n-1]
case 2. n-1번집을 안털었으면 n번집까지 털 수 있으니까 dp[n-2] + dp[n]
이 중에 더 큰값이 된다.
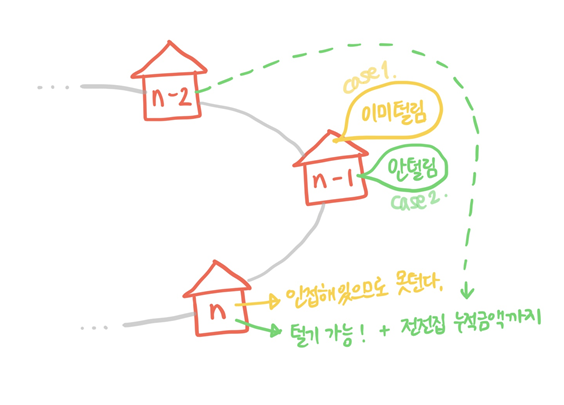
식으로 나타내면 다음과 같다.
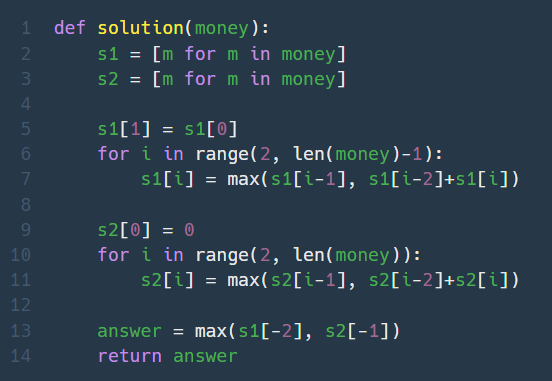
dp[n] = max(dp[n-1], dp[n-2]+dp[n])이런 흐름으로 1, 2번 경우를 모두 구하면, 1번 경우에는 마지막에서 2번째 집 차례에 최대로 턴 금액인 dp[-2]를, 2번 경우에는 마지막집 차례에 최대로 턴 금액인 dp[-1]를 가져와서 비교했을 때 더 큰 값이 답이 된다.
느낀점
- DP에 사용할 규칙을 찾아내면 정작 코드는 비교적 간단한 경우가 많은 것 같다. (모든 코테 문제가 다 그렇겠지만)
- 주어진 문제를 가능한 가장 작은 범위로 쪼개 -아주 그냥 밑바닥까지 쪼개- 생각을 시작하고, 범위를 늘려가면서 아까 구한 값을 어떻게 재활용할 수 있을지 따져봐야한다.
- 아까 구한 값을 활용해서 이번 값을 계산하기 위해 사용할 효율적인 자료구조도 생각해야한다. (1차원배열은 기본이고 2차원, 3차원까지도 올라감)
- Top-Down의 재귀호출 방식보다 Bottom-Up 반복문 방식이 익숙하다. (반복문이 끔찍하게 많이 나옴)
- 잘 모르겠어서 풀이를 찾을 때마다 dp는 자주 안나오지만 어렵다, 이런 말들이 많았는데 무슨 뜻인지 알거 같다. 정말 어렵다..... 도대체 5개 푸는데 며칠이 걸린건지 (자주 안나온다니까 다행이기도)
