
레벨0에서는 시간초과로 실패가 뜨는 경우가 없었는데, 레벨1에서는 시간초과로 실패가 많이 떴다. 그중 몇가지를 정리해보려고 한다.
❗제한 조건에 숫자 범위의 최댓값이 눈에 띄게 크면 시간복잡도를 고려할 것을 주의한다.❗
1. 소수 찾기 (에라토스테네스의 체)
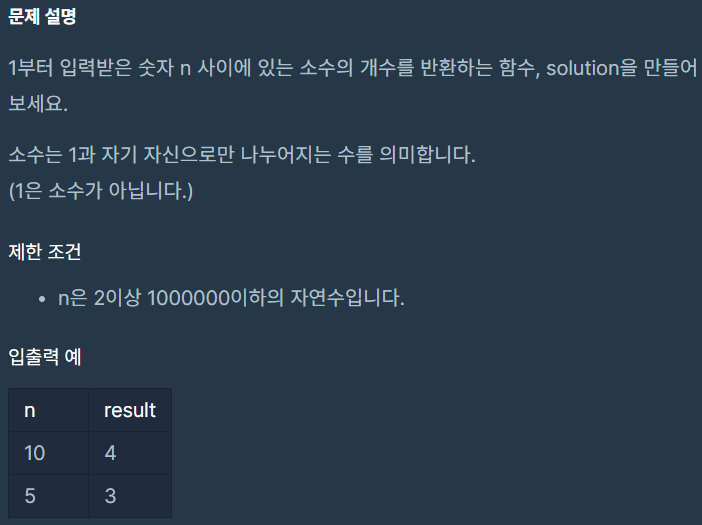
내 코드

소수를 찾는 간단한 문제다. 그래서 처음에는 하나씩 나눠보면서 일일이 약수의 개수를 세가며 소수인지 아닌지 판별했다. 그러나 n의 최댓값이 1000000인 것에서부터 느낌이 오듯이.. 시간초과로 실패가 주르륵 떠버렸고, 이 문제를 풀기 위해서는 '에라토스테네스의 체'를 사용해야 한다는 것을 알았다.
에라토스테네스의 체
에라토스테네스의 체는 자연수 n이하의 모든 소수를 찾는 가장 간단하고 빠른 방법이다.
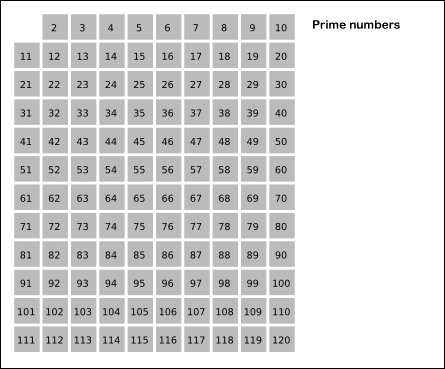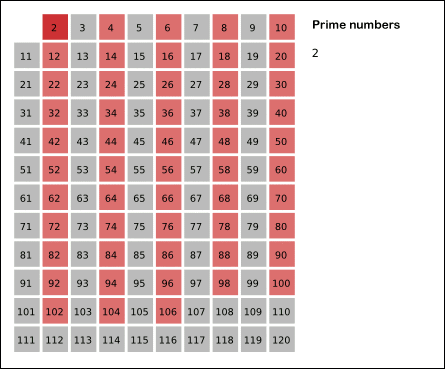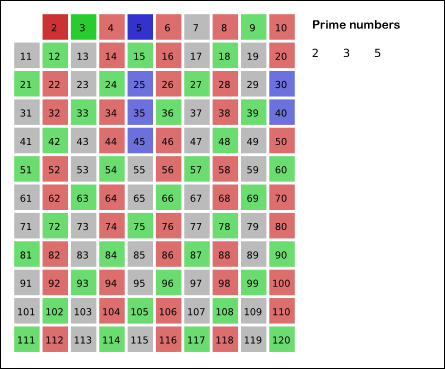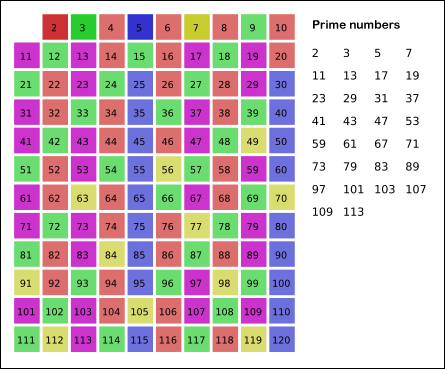
- 알고리즘
(1) 2부터 n까지 숫자를 쭉 쓴다.
(2) 2를 제외한 2의 배수를 제거한다.
(3) 3을 제외한 3의 배수를 제거한다.
(4) 4의 배수는 이미 (2)에서 지워졌으므로 지울 필요 X
(5) 5를 제외한 5의 배수를 제거한다.
...
√n 이하의 수의 배수 제거까지 반복한다.
그리고 남겨진 수들이 n 이하의 소수이다.
이를 소스코드로 옮기면 다음과 같다.
import math
n = 1000 # 2부터 1,000까지의 모든 수에 대하여 소수 판별
array = [True for i in range(n + 1)] # 처음엔 모든 수가 소수(True)인 것으로 초기화
# 에라토스테네스의 체 알고리즘
for i in range(2, int(math.sqrt(n)) + 1): # 2부터 n의 제곱근까지의 모든 수를 확인하며
if array[i] == True: # i가 소수인 경우 (남은 수인 경우)
# i를 제외한 i의 모든 배수를 지우기
j = 2
while i * j <= n:
array[i * j] = False
j += 1
# 모든 소수 출력
for i in range(2, n + 1):
if array[i]:
print(i, end=' ')에라토스테네스의 체가 뭔지 찾아보고도 코드 구현을 어떻게 할지 몰라서 비효율적인 방법으로 한 듯한데, 다음에는 위와 같은 정석적인 코드로 구현해야겠다.
2. 기사단원의 무기 (약수의 개수)

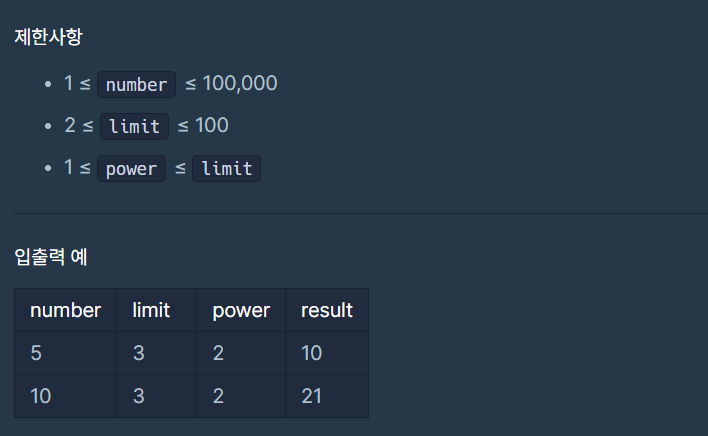
내 코드

얘도 어려운 문제는 아닌데 자꾸 시간초과로 실패가 떴다. 문제의 요점은 간단하게 1부터 n까지 모든 수의 약수의 개수를 구하는 건데, 1부터 1씩 증가해가며 나눠서 나머지가 0인 것을 찾는 논리는 똑같지만 이 범위를 '1부터 n까지'가 아니라 '1부터 √n까지'로 줄여야 통과했다. 그래서 1부터 √n까지의 약수의 개수를 구해서 2배를 한 다음에, n이 제곱수인 경우에만 1을 빼줬다.
3. 숫자 짝꿍 (형변환)

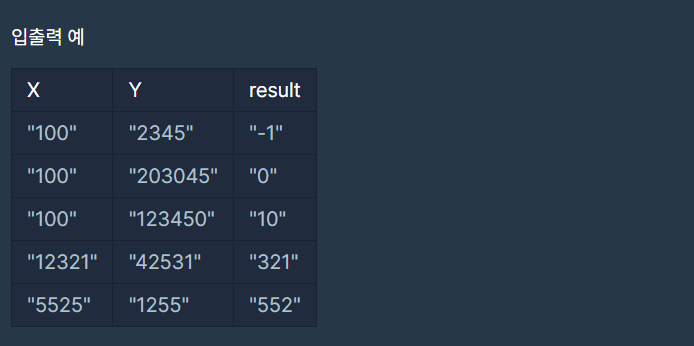
내 코드

결과값이 엄청나게 긴 "000...00"일 때, 이를 if int("000...00") == 0와 같이 형변환을 해서 비교하려고 하면 시간초과가 발생한다. 그래서 해당 문자열이 모두 0으로 이루어져있는지를, 0의 개수와 문자열의 길이를 비교해서 판별하는 코드로 변경해서 통과했다.
4. 달리기 경주 (자료형 메소드)


내 코드
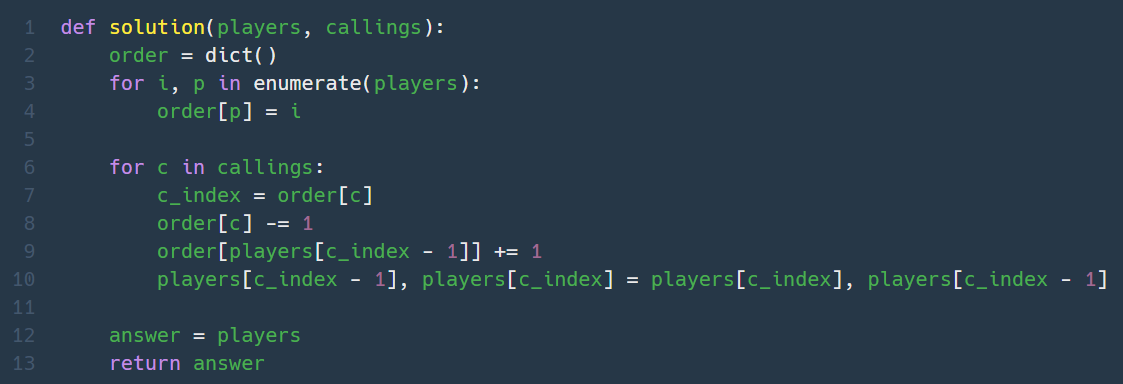
처음엔 선수들의 순위를 리스트 메소드 index()로 구했는데, 얘가 시간초과를 발생시켰다. 그래서 순위 딕셔너리를 따로 만들어서 순위를 가져올때의 시간복잡도가 O(1)이 되도록 변경했더니 통과했다.
이참에 자주 쓰는 메소드들의 시간복잡도를 한번 알아보도록 하자.
리스트 메소드의 시간복잡도
-
O(1)
-arr[i]
-len(arr)
-arr.append(i)
-arr.pop() -
O(N)
-arr.insert(i,v)
-arr.pop(i)
-arr.reverse()
-for i in arr
-i in arr
-arr.count(i)
-arr.index(i)
-del arr[i]
-min(arr)
-max(arr)
-arr.remove(i) -
O(NlogN)
-arr.sort()
번외로 딕셔너리는 key와 value로 바로 접근하기 때문에 반복문 도는 것 외엔 대부분 O(1)이다.
