이진 트리란?

트리는 계층적 구조를 표현하는 비선형 자료구조이다. 이 중 모든 노드의 자식 노드 수가 2개 이하인 조건을 만족하는 트리를 이진 트리 ( Binary Tree, B-tree ) 라고 부른다.

그리고 이진 트리 중에서도 특정 조건들을 추가로 만족하는 트리들을 아래와 같이 세분화할 수 있다.
( 단, 이진 트리는 반드시 하나의 종류에만 속한 것이 아니라 여러 종류에 동시에 속할 수 있다 )

이진 트리 종류

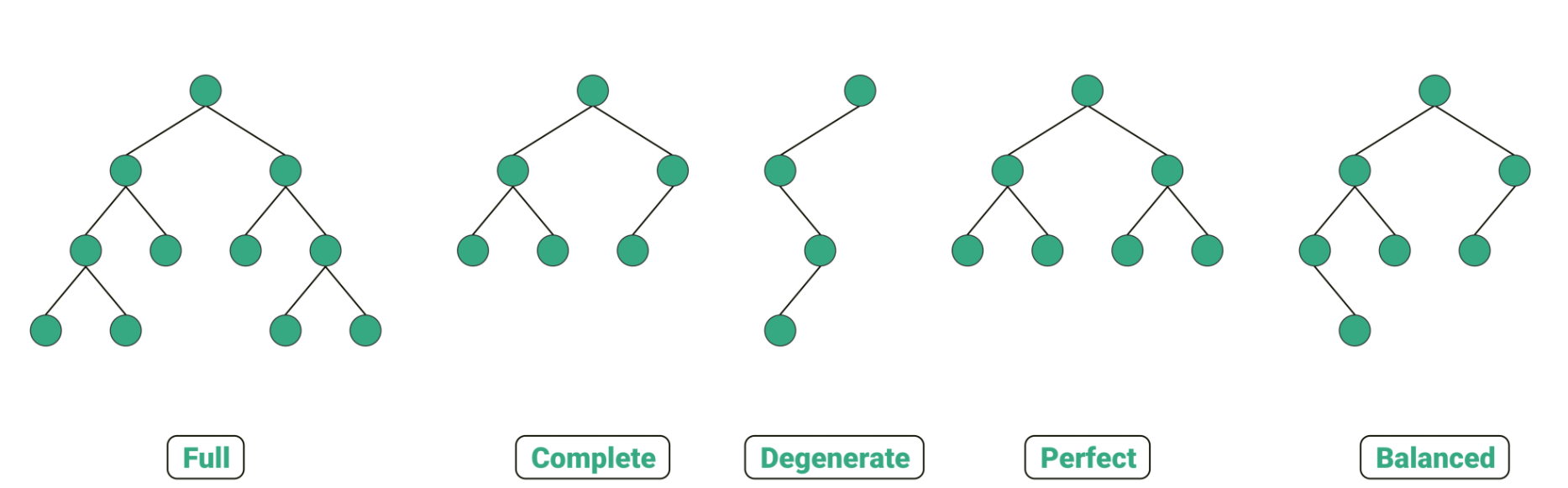
포화 이진 트리 ( Perfect Binary Tree )

조건

• 마지막 레벨을 제외한 모든 노드가 2개의 자식 노드를 지니고 있어야 한다.

결과

• 노드의 수: 2^h - 1
• 단말 노드에서 루트 노드까지의 거리가 모두 동일하다.
• 단말 노드는 모두 같은 레벨에 속한다.

완전 이진 트리 ( Complete Binary Tree )

조건

• 마지막 레벨을 제외한 부분 트리는 포화 이진 트리의 조건을 만족한다. 단, 마지막 레벨의 노드는 반드시 왼쪽 노드부터 차례로 채워져야한다.

결과

• Heap은 완전 이진 트리의 자료구조를 따른다.
• Array를 통해 구현하는 것이 편하다.
  ( i, 2i + 1, 2i + 2 ) -> ( 루트 노드, 왼쪽 자식 노드, 오른쪽 자식 노드 )
• 최소 노드: 2^(h-1)
• 최대 노드: 2^h - 1
  ( 포화 이진 트리 )

편향 이진 트리 ( Degenerate/skewed Tree )

조건

• 모든 내부 노드는 하나의 자식 노드만 가져야한다.
  ( Skewed Tree의 경우는 한 방향으로만 자식 노드를 가져야한다 )

결과

• Linked List와 사실상 같은 구조를 지닌다.
• 노드의 수: h
• BST에서 이 문제로 인해 RBT( RED BLACK TREE )가 생겼다.

정 이진 트리 ( Full Binary Tree )

조건

• 모든 노드가 자식노드를 가지지 않거나, 2개의 자식노드를 가져야한다.
  ( 1개만 지니는 경우 조건 위배 )
  ( 단말 노드를 제외한 모든 노드는 2개의 자식 노드를 가져야함 )

결과

• 자식 노드 수: 내부 노드 + 1

균형 이진 트리 ( Balanced Binary Tree )

조건

• 모든 단말 노드 레벨 간의 차가 1보다 작거나 같아야한다.

결과

• h: Math.floor(log(n))
• RBT의 경우, 최종적인 목적은 균형 이진 트리를 벗어나지 않기 위함이다.
• 균형 이진 트리를 위배하는 경우 각 노드를 탐색하는 속도가 저하된다.