트리와 그래프에 대한 이해 → 복잡한 문제 해결
e.g. 데이터베이스(B-트리), 데이터 인코딩/압축(허프만 트리), 그래프 컬러링, 할당 문제, 최소 거리 문제 등
계층적 문제
- 회사 조직도
- 교과 과정 계층도
순환 종속성
- 관계도(SNS 친구 관계)
- 도로망
Tree
모든 노드는 자식 노드가 없거나 하나 이상의 자식 노드를 가질 수 있다.
루트 노드를 제외한 모든 노드는 하나의 부모 노드를 가진다.
어떤 노드의 degree는 그 노드가 가진 자식 노드의 수를 말한다.
같은 노드를 부모 노드를 가지는 노드들은 sibling이라 표현
degree에 따라서 leaf 노드인지 internal 노드인지 구별한다.
경로(Path)
edge의 개수는 경로의 길이
Depth
노드의 depth는 루트로부터의 해당 노드까지의 길이를 말한다. → 루트에서 그 노드까지의 경로의 길이 → edge의 개수
Height
가장 큰 depth → 트리의 Height
e.g. 루트 노드 하나라면 0, empty tree는 -1
Ancestor and Descendant
자기 자신은 조상이면서 자손
루트 노드는 모든 노드의 조상 ancestor
트리 순회
- 전위 순회(preorder traversal)
-
Current Node→Left→Right
preorder(전위 순회)(노드 주소) if 인자로 전달된 노드 주소가 없다면 종료 노드의 값 출력 또는 전달 preorder(노드의 왼쪽에 연결견된 주소) preorder(노드의 오른쪽에 연결된 주소)
-
- 중위 순회(inorder traversal)
-
Left→Current Node→Right
inorder(중위 순회)(노드 주소) if 인자로 전달된 노드 주소가 없다면 종료 inorder(노드의 왼쪽에 연결견된 주소) 노드의 값 출력 또는 전달 inorder(노드의 오른쪽에 연결된 주소)
-
- 후위 순회(postorder traversal)
-
Left→Right→Current Node
postorder(중위 순회)(노드 주소) if 인자로 전달된 노드 주소가 없다면 종료 postorder(노드의 왼쪽에 연결견된 주소) postorder(노드의 오른쪽에 연결된 주소) 노드의 값 출력 또는 전달
-
- 레벨 순서 순회(level order traversal)
-
트리의 맨 위 레벨부터 아래 레벨까지, 왼쪽 노드에서 오른쪽 노드 순서로 방문. 트리의 루트 노드부터 단계별로 차례대로 나열하는 것과 같다.
레벨 순서 순회(level order traversal)(노드 주소) if 노드 주소가 없다면 종료 큐 생성 후 노드 주소 할당 while 큐가 비어있지 않으면 for 큐의 크기만큼 큐에서 노드를 꺼내고 current에 저장 current 노드의 값을 출력 또는 반환 if current 노드의 left에 노드 존재 확인 있으면 큐에 저장 if current 노드의 right에 노드 존재 확인 있으면 큐에 저장
-
다양한 트리 구조
- 이진 검색 트리 BST, binary search tree
- 특징
- 부모 노드의 값 ≥ 왼쪽 자식 노드의 값
- 부모 노드의 값 ≤ 오른쪽 자식 노드의 값
- BST가 마지막 레벨을 제외한 모든 노드에 두 개의 자식 노드가 있을 경우, 이 트리의 높이는 이 되고 은 원소의 개수이다. 이로서 BST 검색 및 삽입 동작은 의 시간 복잡도를 갖는다. (complete binary tree)
- 이진 트리 다양한 형태들
- Full Binary Tree
- 모든 노드가 자식이 없거나 2개의 자식을 가지고 있다. the number of internal nodes - the total number of nodes - number of leaves - number of levels -
- 레벨 L의 트리의 높이(height)는
- leaf 노드 수는
- 전체 노드 수는
- internal 노드 수는
- 총 노드 수
- 총 internal 노드 수는
- leaf 노드의 가장 많을 때는
- 모든 노드가 자식이 없거나 2개의 자식을 가지고 있다. the number of internal nodes - the total number of nodes - number of leaves - number of levels -
- Complete Binary Tree
- 모든 leaf 노드들은 같은 level에 있으면서(같은 depth를 가지면서) 왼쪽면에서 채워지는 트리. 마지막 레벨을 제외한 레벨은 full
- depth에서 complete binary tree의 노드 수는
- 개의 노드를 가진 complete binary tree의 높이는
- 모든 leaf 노드들은 같은 level에 있으면서(같은 depth를 가지면서) 왼쪽면에서 채워지는 트리. 마지막 레벨을 제외한 레벨은 full
- Perfect Binary Tree
- internal 노드들 모두 두 자식 노드들을 가지고 있으며 모든 leaf 노드들은 같은 level에 있다.
- 높이의 perfect binary tree는 개의 노드들을 갖는다.
- internal 노드들 모두 두 자식 노드들을 가지고 있으며 모든 leaf 노드들은 같은 level에 있다.
- Full Binary Tree
- 특징
구현
원소 검색
노드 주소 find(찾는 값, 노드 주소)
if 노드 주소가 없다면
종료 또는 현재 노드 반환(insert 함수 때 재사용시)
if 노드 주소의 값 == 찾는 값
노드 주소 반환
if 노드 주소의 값 > 찾는 값
find(찾는 값, 노드 오른쪽 주소) 함수 반환
find(찾는 값, 노드 왼쪽 주소) 함수 반환원소 삽입
insert(값)
if root가 없으면
root에 값 저장
else
_insert(root, 값)
_insert(노드, 값)
if 값 < 노드의 값
if 노드의 왼쪽이 없으면
노드의 왼쪽에 노드 생성 후 값 저장
else
_insert(노드의 왼쪽 주소, 값)
else
if 노드의 오른쪽이 없으면
노드의 오른쪽에 노드 생성 후 값 저장
else
_insert(노드의 오른쪽 주소, 값)
---------------------------------
insert(값)
find(값, 루트) 반환된 주소 값에 노드 생성 후 값 저장원소 삭제 - 여러 방식이 있다.
/* 자식 노드가 없는 경우
* -> 단순 삭제
* 자식 노드가 하나만 있는 경우
* -> 노드 삭제 후 부모 노드의 포인터가 해당 자식 노드를 가리키게 한다.
* 자식 노드가 두 개 있는 경우
* -> 노드 삭제 후, 현재 노드를 후속 노드로 대체
* -> successor를 구할지 predecessor를 구하는 건 마음이 가는대로.
*/
/* 전임자냐 후임자냐 == 삭제하는 노드의 값 바로 전의 값이나 후의 값으로 교체할지 결정 */
노드 successor(노드) // Left-most child of the right subtree of the target node
current 노드 변수에 노드의 오른쪽 주소를 저장
while(current가 없으면서 current의 왼쪽이 없으면)
current에 current의 왼쪽 주소 저장
current 반환 // successor 노드 반환
노드 predecessor(노드) // Right-most child of the left subtree of the target node
current 노드 변수에 노드의 왼쪽 주소를 저장
while(current가 없으면서 current의 오른쪽이 없으면)
current에 current의 오른쪽 주소 저장
current 반환 // predecessor 노드 반환
----------------------------------------------
노드 delete(노드, 찾는 값)
if 찾는 값 < 노드의 값
노드의 왼쪽 = delete(노드의 왼쪽, 찾는 값)
else if 찾는 값 > 노드의 값
노드의 오른쪽 = delete(노드의 오르쪽, 찾는 값)
/* 위의 코드는 원소 검색 함수로 재사용 가능하다 */
/* if find(노드)의 반환 값이 NULL이라면 NULL 반환 */
else
if 노드의 left가 없다면 // 자식 노드가 전혀 없거나, 왼쪽 자식 노드만 없는 경우
노드의 오른쪽 주소를 변수에 저장
노드 삭제
저장한 주소 값 반환
if 노드의 right가 없다면 // 오른쪽 자식 노드만 없는 경우
노드의 왼쪽 주소를 변수에 저장
노드 삭제
저장한 주소 값 반환
// 자식 노드가 둘 다 있는 경우
노드의 후속노드를 가져와서 노드의 데이터에 후속노드의 데이터를 저장
// 오른쪽 서브 트리에서 후속노드 찾아 삭제
노드의 오른쪽에 delete(노드의 오른쪽, 후속노드의 데이터) 함수 반환 값 저장
노드 반환
----------------------------------------------
트리 연산 시간 복잡도
- BST 검색에 필요한 시간 T(N) = T(N/2) + 1 = O(\log N)
- Complete binary tree가 아닌 한 이 시간 복잡도는 항상 성립하지 않는다.
- 균형 이진 트리가 이 문제를 해결
균형 balanced trees
문제는 BST가 어떻게 데이터가 삽입됐냐에 따라서 효율성이 나뉜다.
→ 최악의 경우 연결 리스트, 최상의 경우 complete binary tree
기준 노드의 양쪽 서브트리의 높이(h)의 차가 -1, 0, 1인 경우 balanced 균형잡힌 상태라 한다.
-
용어
- mountain - 양쪽 노를 가지고 있는 형태
- stick - 한방향 + 하나의 자식 노드만으로 이루어진 형태
- rotation - 회전
- balance factor - 두 서브트리 높이의 차. 여기서는 ‘BF = RSH - LSH’로 계산.
- elbow - 하나의 자식 노드들로 이루어졌으며 오른쪽 자식 노드에서 왼쪽 자식노드를 가진 형태(팔 구부린 형상)
-
목표
- balance factor가 큰 stick이나 elbow 형태인 트리를 rotation하여 mountain 형태로 변형
-
Rotations
-
balance factor를 구하고 거기에 맞춰서 회전을 하여 균형있는 형태로 변형
-
Left Rotation
- BF = RSH(2) - LSH(0) = 2 & BF = RSH(1) - LSH(0) = 1
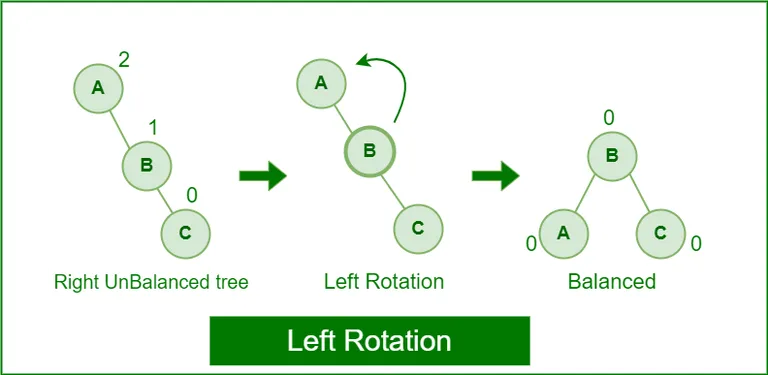
- BF = RSH(2) - LSH(0) = 2 & BF = RSH(1) - LSH(0) = 1
-
Right Rotation
- BF = RSH(0) - LSH(2) = -2 & BF = RSH(0) - LSH(1) = -1
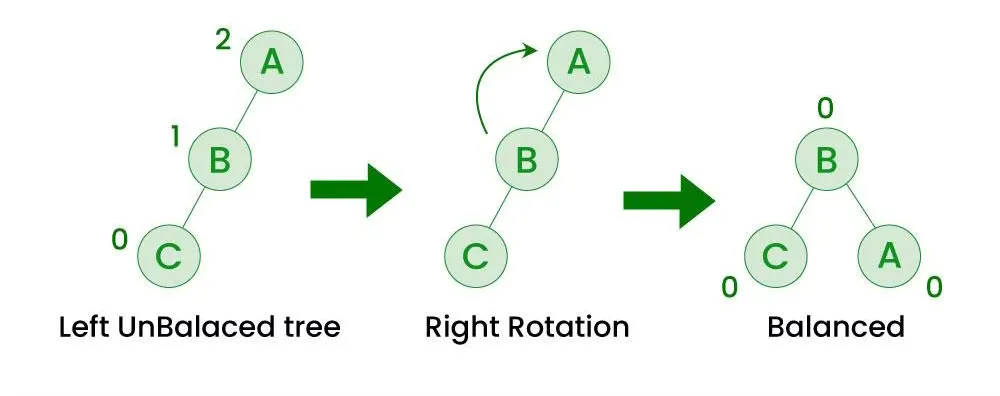
- BF = RSH(0) - LSH(2) = -2 & BF = RSH(0) - LSH(1) = -1
-
Left-Right Rotation
- BF = RSH(0) - LSH(2) = -2 & BF = RSH(1) - LSH(0) = 1
- elbow → stick → mountain
-
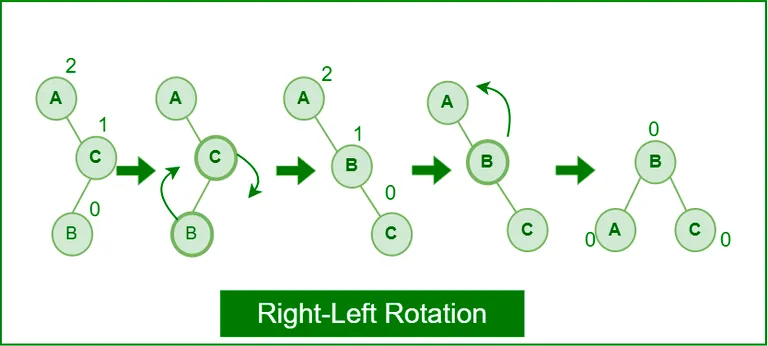
Right-Left Rotation
- BF = RSH(2) - LSH(0) = 2 & BF = RSH(0) - LSH(1) = -1
- elbow → stick → mountain
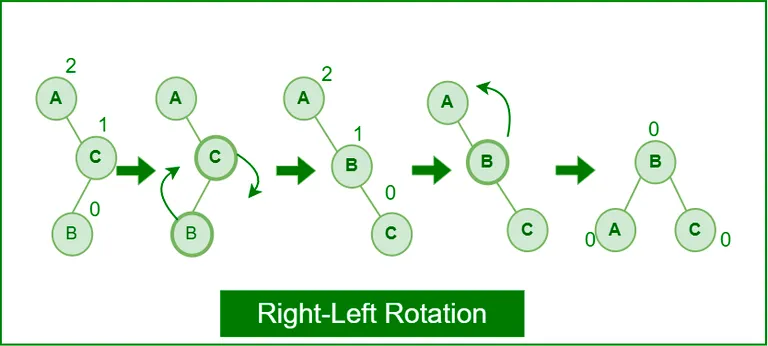
-
-
Rotation summary - BF = RSH - LSH로 한 표. LSH - RSH로 했을 때는 부호를 바꾸면 된다.
Balance factor of the lowest point of imbalance Balance factor of the node in the direction of imbalance Left Rotation 2 1 Right Rotation -2 -1 L-R Rotat -2 1 R-L Rotation 2 -1 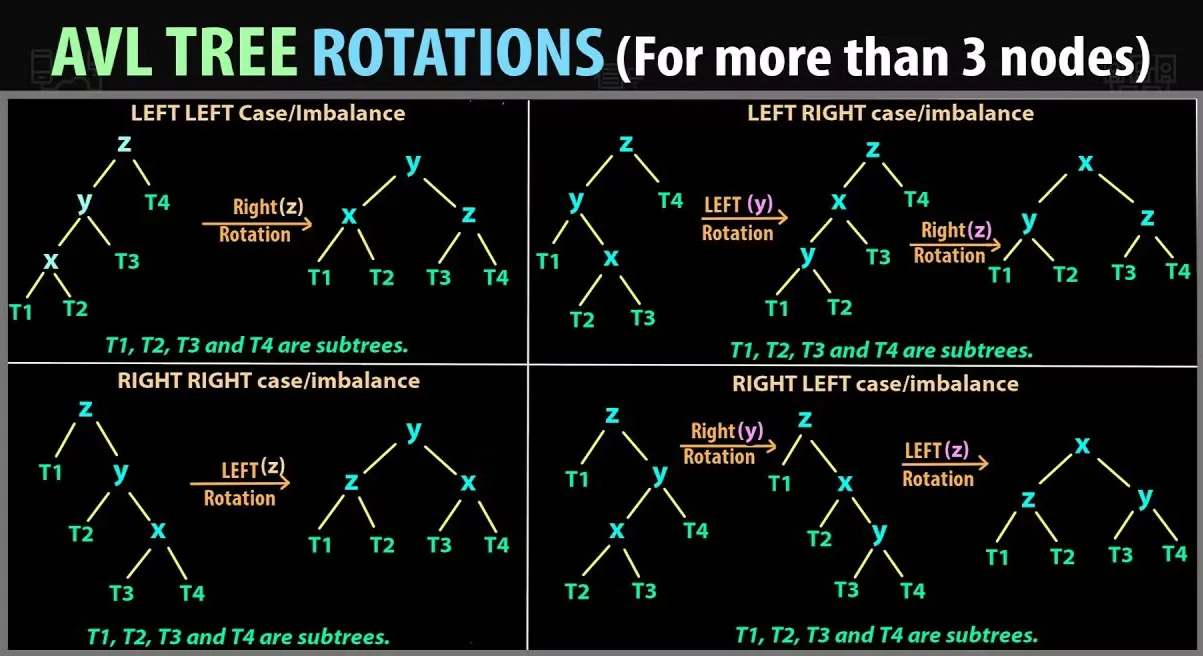
위의 균형 트리를 AVL 트리라 한다.
- 이진 트리와 같다. 다만, 삽입과 삭제에서 더 많은 작업을 해야한다.
- 어떤 작업?
- balance factor를 빠르게 계산하기 위해 각 노드의 높이를 저장
- 삽입 및 삭제시 회전하고 새로 높이를 업데이트한다.
- 어떤 작업?
- 연산
- 탐색 - BST와 같다.
- 삽입 - BST와 같이 삽입하고 Balance Factor를 체크한 후 -1, 0 또는 1이 아닌 경우 Rotation 한다.
- 삭제 - BST와 같이 선임자 노드를 찾고 swap한 후 삭제하고 Balance Factor를 체크한 후 -1, 0 또는 1일 경우 Rotation한다.
코드 설명 : 기본 bst로 만든 dictionary 코드와 비교
BST
/* ADT */
template<typename K, typename D>
class Dictionary
{
public:
Dictionary();
const D& find(const K& key);
void insert(const K& key, const D& data);
const D& remove(const K& key);
const D& max() const;
const D& min() const;
void print();
private:
class TreeNode
{
public:
const K& key;
const D& data;
TreeNode* left;
TreeNode* right;
TreeNode(const K& key, const D& data);
};
TreeNode* root_;
// all in private to hide the information
const D& _max(TreeNode* cur) const;
const D& _min(TreeNode* cur) const;
TreeNode*& _find(const K& key, TreeNode*& cur) const;
const D& _remove(TreeNode*& node);
TreeNode*& _predecessor(TreeNode*& cur) const;
TreeNode*& _successor(TreeNode*& cur) const;
TreeNode*& _rightmost(TreeNode*& cur) const;
TreeNode*& _leftmost(TreeNode*& cur) const;
TreeNode*& _swap(TreeNode*& node1, TreeNode*& node2);
};/* key값으로 node 찾기 */
template <typename K, typename D>
const D& Dictionary<K, D>::find(const K& key)
{
TreeNode*& node = _find(key, root_);
if (node == nullptr) throw std::runtime_error("Error: key not found in _find()");
return node->data;
}
template<typename K, typename D>
typename Dictionary<K, D>::TreeNode*& Dictionary<K, D>::_find(const K& key, TreeNode*& cur) const
{
if (cur == nullptr || key == cur->key)
return cur;
else if (key < cur->key)
return _find(key, cur->left);
else
return _find(key, cur->right);
}
/* find() 함수로 노드를 찾고 삽입하기 */
template <typename K, typename D>
void Dictionary<K, D>::insert(const K& key, const D& data)
{
TreeNode*& node = _find(key, root_);
node = new TreeNode(key, data);
}
/* key값으로 노드 삭제 */
template <typename K, typename D>
const D& Dictionary<K, D>::remove(const K& key)
{
TreeNode*& node = _find(key, root_);
return _remove(node);
}
template<typename K, typename D>
const D& Dictionary<K, D>::_remove(TreeNode*& node)
{
std::cout << std::endl;
if (!node) {
throw std::runtime_error("Error: _remove() used on non-existent key");
}
if (node->left == nullptr ) {
const D& data = node->data;
TreeNode* tmp = node;
node = node->right;
delete tmp;
return data;
}
if (node->right == nullptr) {
const D& data = node->data;
TreeNode* tmp = node;
node = node->left;
delete tmp;
return data;
}
TreeNode*& predecessor = _predecessor(node);
// TreeNode*& successor = _successor(node);
if (!predecessor)
throw std::runtime_error("Error: predecessor not found");
TreeNode *&moved_node = _swap(node, predecessor);
return _remove(moved_node);
}
template <typename K, typename D>
typename Dictionary<K, D>::TreeNode*& Dictionary<K, D>::_predecessor(TreeNode*& cur) const
{
if (!cur)
return cur;
if (!(cur->left))
return cur->left;
return _rightmost(cur->left);
}
template <typename K, typename D>
typename Dictionary<K, D>::TreeNode*& Dictionary<K, D>::_successor(TreeNode*& cur) const
{
if (!cur)
return cur;
if (!(cur->right))
return cur->right;
return _leftmost(cur->right);
}
template <typename K, typename D>
typename Dictionary<K, D>::TreeNode*& Dictionary<K, D>::_rightmost(TreeNode*& cur) const
{
if (!cur || !(cur->right))
return cur;
return _rightmost(cur->right);
}
template <typename K, typename D>
typename Dictionary<K, D>::TreeNode*& Dictionary<K, D>::_leftmost(TreeNode*& cur) const
{
if (!cur || !(cur->left))
return cur;
return _leftmost(cur->left);
}
template <typename K, typename D>
typename Dictionary<K, D>::TreeNode*& Dictionary<K, D>::_swap(TreeNode*& node1, TreeNode*& node2)
{
// for _predecessor()
if (node1->left == node2) {
TreeNode *tmp = node2;
std::swap(node1->right, node2->right);
node1->left = tmp->left;
tmp->left = node1;
node1 = tmp;
return node1->left;
}
// for _successor()
if (node1->right == node2)
{
TreeNode *tmp = node2;
std::swap(node1->left, node2->left);
node1->right = tmp->right;
tmp->right = node1;
node1 = tmp;
return node1->right;
}
std::swap(node1->left, node2->left);
std::swap(node1->right, node2->right);
std::swap(node1, node2);
return node2;
}/* 나머지 함수들의 body */
/** constructor of Dictionary class */
template <typename K, typename D>
Dictionary<K, D>::Dictionary()
: root_(nullptr)
{}
/** constructor of TreeNode class in Dictionary class */
template <typename K, typename D>
Dictionary<K, D>::TreeNode::TreeNode(const K& key, const D& data)
: key(key), data(data), left(nullptr), right(nullptr)
{}
/** the right-most data of the tree */
template <typename K, typename D>
const D& Dictionary<K, D>::max() const { return _max(root_); }
/** the left-most data of the tree */
template <typename K, typename D>
const D& Dictionary<K, D>::min() const { return _min(root_); }
template <typename K, typename D>
const D& Dictionary<K, D>::_max(TreeNode* cur) const
{
while (cur && cur->right)
cur = cur->right;
return cur->data;
}
template <typename K, typename D>
const D& Dictionary<K, D>::_min(TreeNode* cur) const
{
while (cur && cur->left)
cur = cur->left;
return cur->data;
}AVL 트리 - ADT, 삽입, 삭제
template<typename K, typename D> // key & data
class AVL
{
public:
AVL() : head_(nullptr) {}
const D& find(const K& key);
bool contains(const K& key);
void insert(const K& key, const D& data);
const D& remove(const K& key);
bool empty() const;
void clear();
private:
class Node
{
public:
const K &key;
const D &data;
Node *left;
Node *right;
int height;
Node(const K &key, const D &data) : key(key), data(data), left(nullptr), right(nullptr), height(0) {}
};
Node* head_;
Node*& _find(const K& key, Node*& cur) const;
void _find_and_insert(const K& key, const D& data, Node*& cur);
const D& _find_and_remove(const K& key, Node*& cur);
const D& _remove(Node*& node);
// 삭제를 위해 삭제할 노드와 스왑할 in-order의 전임자를 찾기 위한 함수들
const D& _iopRemove(Node*& targetNode);
const D& _iopRemove(Node*& targetNode, Node*& iopAncester, bool isInitialCall);
Node*& _swap_nodes(Node*& node1, Node*& node2);
void _updateHeight(Node*& cur);
void _ensureBalance(Node*& cur);
void _rotateLeft(Node*& cur);
void _rotateRight(Node*& cur);
void _rotateLeftRight(Node*& cur);
void _rotateRightLeft(Node*& cur);
int _get_height(Node*& node) const;
int _get_balance_factor(Node*& node) const;
};삽입
// BST와 같지만 Balance Factor를 계산해야한다.
template <typename K, typename D>
void AVL<K, D>::_find_and_insert(const K& key, const D& data, Node*& cur)
{
if (!cur) {
cur = new Node(key, data);
return;
}
else if (cur->key == key) {
throw std::runtime_error("ERROR::INSERT::key already exists");
}
else if (cur->key > key) {
_find_and_insert(key, data, cur->left);
_ensureBalance(cur);
return ;
}
else {
_find_and_insert(key, data, cur->right);
_ensureBalance(cur);
}
}
template <typename K, typename D>
void AVL<K, D>::_ensureBalance(Node*& cur)
{
if (!cur) return;
// cur 노드의 balance factor 계산
int initial_balance = _get_balance_factor(cur);
// balance를 확인하고 불균형인 곳이 있으면 그곳의 방향을 찾아 회전시킨다.
if (initial_balance == -2)
{
const int left_balance = _get_balance_factor(cur->left);
if ((left_balance == -1) || (left_balance == 0))
_rotateRight(cur);
else if (left_balance == 1)
_rotateLeftRight(cur);
else
// error check;
}
else if (initial_balance == 2)
{
const int right_balance = _get_balance_factor(cur->right);
if ((right_balance == 1) || (right_balance == 0))
_rotateLeft(cur);
else if (right_balance == -1)
_rotateRightLeft(cur);
else
// error check;
}
// 높이를 업데이트
_updateHeight(cur);
// 마지막 error check
const int final_balance = _get_balance_factor(cur);
if (final_balance < -1 || final_balance > 1)
{
//error check
}
}
template <typename K, typename D>
void AVL<K, D>::_updateHeight(TreeNode*& cur)
{
if (!cur) return;
cur->height = 1 + std::max(_get_height(cur->left), _get_height(cur->right));
}
int _get_height(TreeNode*& node) const
{
if (!node)
return -1;
else
return node->height;
}삭제
template <typename K, typename D>
const D &AVL<K, D>::_find_and_remove(const K& key, Node*& cur)
{
if (!cur) throw std::runtime_error("ERROR::FIND_AND_REMOVE::key not found");
else if (cur->key == key) return _remove(cur);
else if (cur->key < key)
{
const D& data = _find_and_remove(key, cur->right);
_ensureBalance(cur);
return data;
}
else
{
const D& data = _find_and_remove(key, cur->left);
_ensureBalance(cur);
return data;
}
}
template <typename K, typename D>
const D& AVL<K, D>::_remove(Node*& node)
{
if (!node) throw std::runtime_error("ERROR::REMOVE::the function used on nullptr");
if (!node->left && !node->right) // 자식이 없을때
{
const D& data = node->data;
delete node;
node = nullptr;
return data;
}
else if (node->left && !node->right) // 왼쪽만
{
const D& data = node->data;
Node* temp = node;
node = node->left;
delete temp;
temp = nullptr;
return data;
}
else if (!node->left && node->right) // 오른쪽만
{
const D& data = node->data;
Node* temp = node;
node = node->right;
delete temp;
temp = nullptr;
return data;
}
else // 둘다
{
return _iopRemove(node);
}
}
// 선임자 찾는 함수들
template <typename K, typename D>
const D& AVL<K, D>::_iopRemove(Node*& targetNode)
{
if (!targetNode) throw std::runtime_error("ERROR::IOP_REMOVE:: this function called on nullptr");
const D& data = _iopRemove(targetNode, targetNode->left, true);
if (targetNode->left)
_ensureBalance(targetNode->left);
_ensureBalance(targetNode);
return data;
}
template <typename K, typename D>
const D& AVL<K, D>::_iopRemove(Node*& targetNode, Node*& iopAncester, bool isInitialCall)
{
if (!targetNode) throw std::runtime_error("ERROR::IOP_REMOVE:: targetNode is nullptr");
if (!iopAncester) throw std::runtime_error("ERROR::IOP_REMOVE:: iopAncester is nullptr");
if (!iopAncester->right)
{
const D &data = _iopRemove(targetNode, iopAncester->right, false);
if (!isInitialCall)
if (iopAncester)
_ensureBalance(iopAncester);
return data;
}
else
{
Node*& movedTarget = _swap_nodes(targetNode, iopAncester);
const D& data = _remove(movedTarget);
return data;
}
}
// 선임자를 찾고 그 노드와 삭제할 노드 스왑
template <typename K, typename D>
typename AVL<K, D>::Node*& AVL<K, D>::_swap_nodes(Node*& node1, Node*& node2)
{
Node* orig_node1 = node1;
Node* orig_node2 = node2;
std::swap(node1->height, node2->height);
if (node1->left == node2)
{
std::swap(node1->right, node2->right);
node1->left = orig_node2->left;
orig_node2->left = node1;
node1 = orig_node2;
return node1->left;
}
else if (node1->right == node2)
{
std::swap(node1->left, node2->left);
node1->right = orig_node2->right;
orig_node2->right = node1;
node1 = orig_node2;
return node1->right;
}
else if (node2->left == node1)
{
std::swap(node2->right, node1->right);
node2->left = orig_node1->left;
orig_node1->left = node2;
node2 = orig_node1;
return node2->left;
}
else if (node2->right == node1)
{
std::swap(node2->left, node1->left);
node2->right = orig_node1->right;
orig_node1->right = node2;
node2 = orig_node1;
return node2->right;
}
else
{
std::swap(node1->left, node2->left);
std::swap(node1->right, node2->right);
std::swap(node1, node2);
return node2;
}
}https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
구현 후 비교하면서 에러 체크.
Left-Leaning Red-Black Tree
모든 레드 블랙 트리는 2-3 또는 2-3-4 트리 구현에 기초한다.
- 재귀적 구현
- 모든 3-노드들은 왼쪽으로 기울게 한다.
- 트리로 올라가면서 Rotation을 수행.
2-3 tree는 3차인 B-tree.
성질
- 두 개의 자식노드를 가지고 있으면 2-node라 한다. 2-node는 하나의 데이터 값과 두 자식 노드를 갖는다.
- 세 개의 자식노드를 가지고 있으면 3-node라 한다. 3-node는 두 데이터 값들과 세 자식 노드를 갖는다.
- 데이터 값은 정렬되어 저장.
- 균형 트리
- 모든 자식 노드는 같은 레벨이다.
Red Black Tree(Left Leaning Red Black Tree)
성질
- 레드 링크는 왼쪽으로 기울어져있다.
- 부모로부터의 연결이 레드 링크면 레드 노드
- 어떤 노드도 레드 링크 두 개와 연결될 수 없다.
- 레드 노드의 자식은 블랙
- null 노드는 블랙
- 루트 노드는 블랙
- 블랙을 기준으로 균형잡혀있다. (레드는 무시)
- 어떤 노드에서 null 노드까지의 모든 경로의 블랙 거리는 같다.
연산(회전, 색 뒤집기)이 일어나는 상황
- 레드 링크가 오른쪽에 있을때(right leaning red link)
- 트리가 편향되었을때 → 같은 방향으로 노드가 계속 추가 되었을때
Insertion
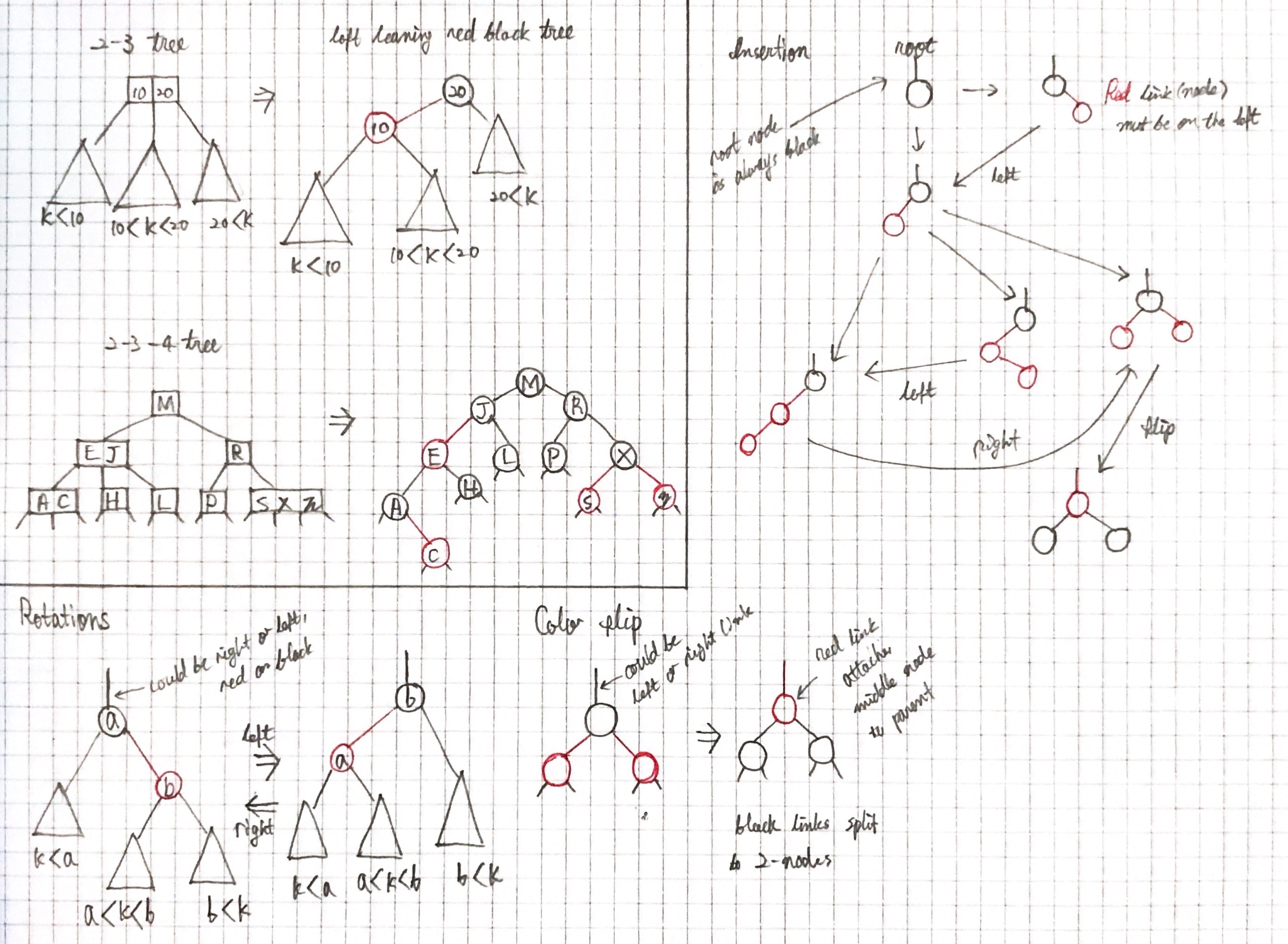
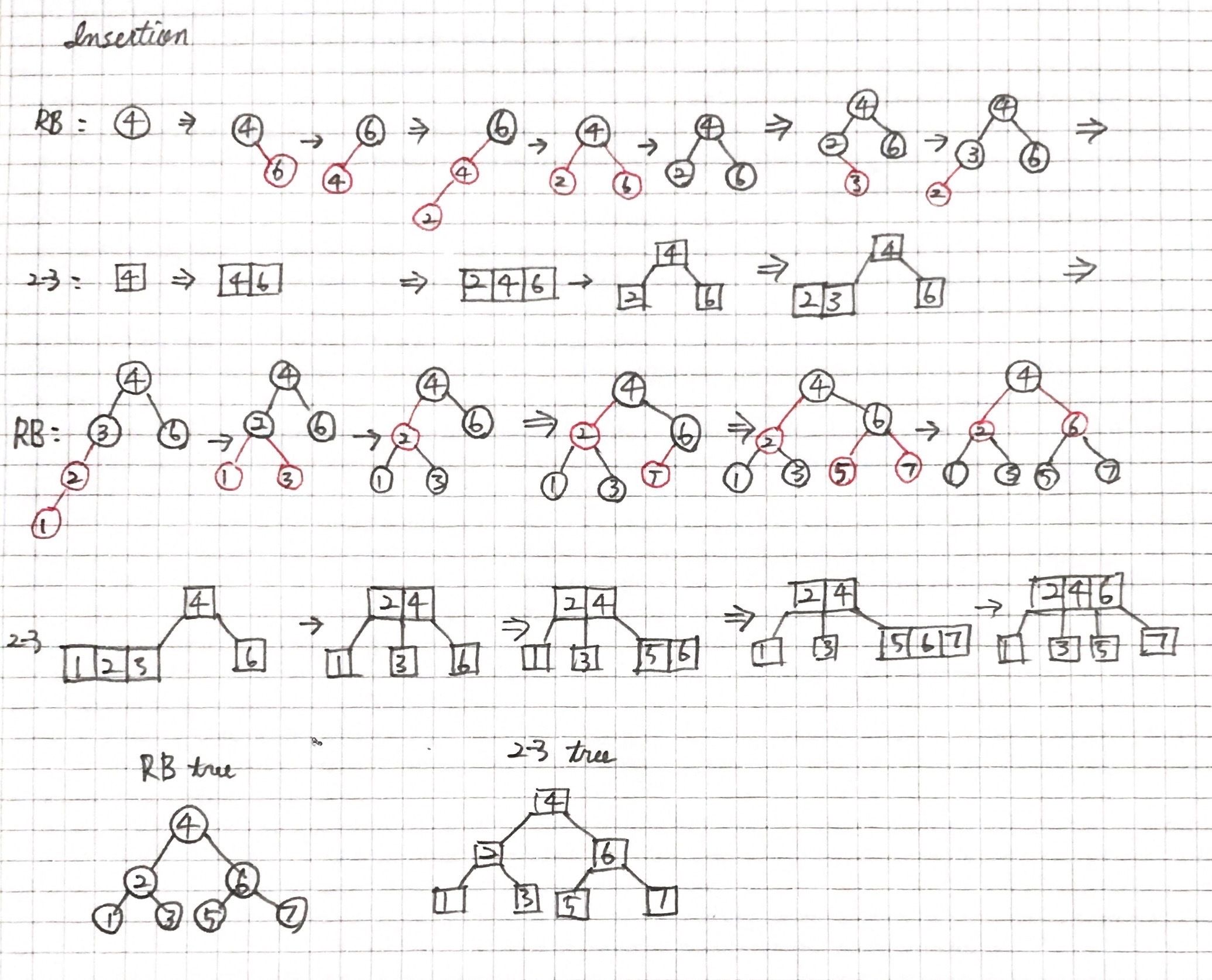
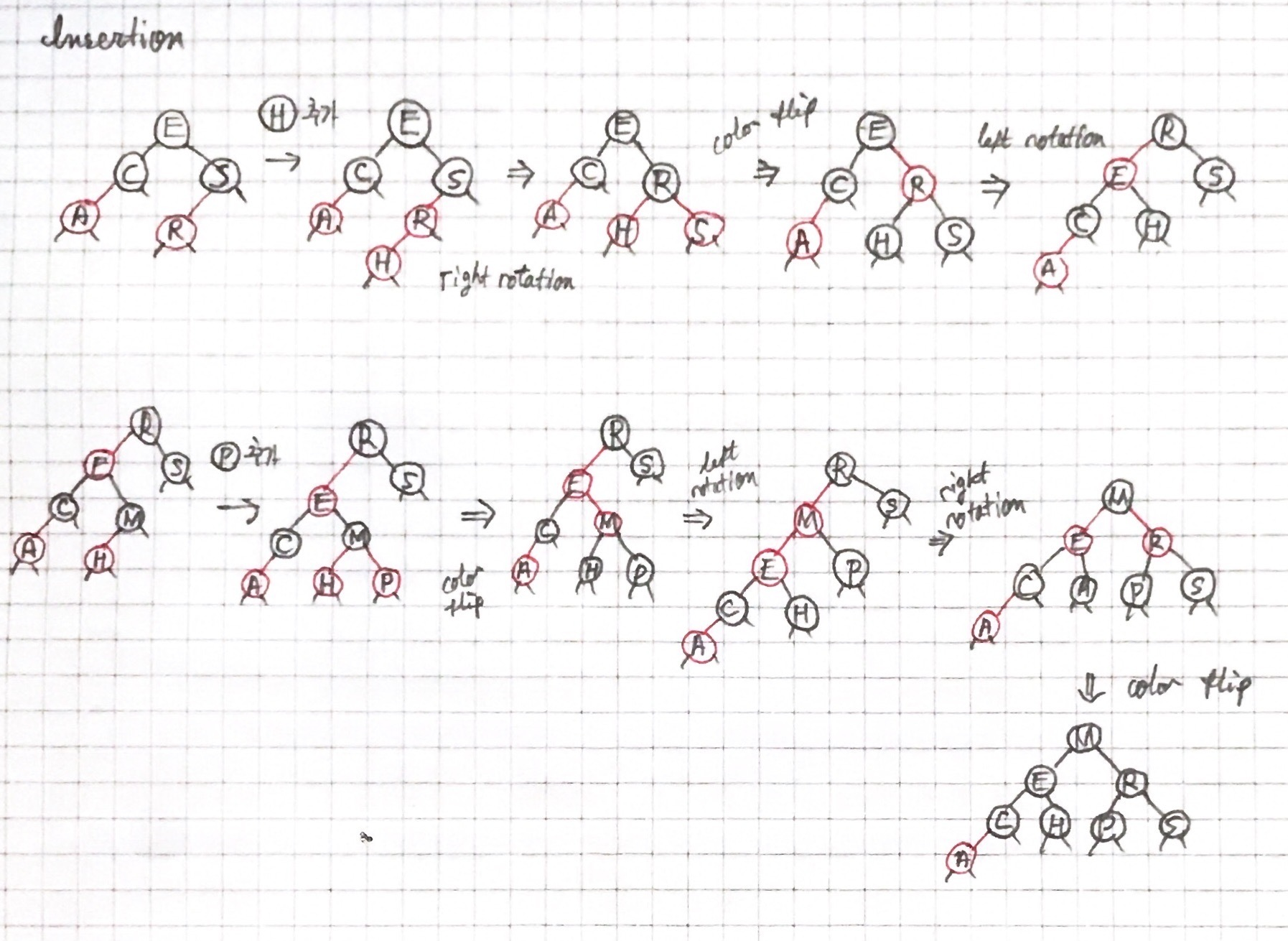
삽입 코드
void insert(const K& key, const D& data);
bool _isRed(Node*& node) const;
void _insert(Node*& node, const K& key, const D& data);
void _balance(Node*& node);
void _rotateRight(Node*& node);
void _rotateLeft(Node*& node);
void _colorFlip(Node*& node);
Color _colorChange(Color c);template <typename K, typename D>
bool RB<K, D>::_isRed(Node*& node) const
{
if (!node) return BLACK; // null(nil) nodes are black.
return node->color == RED;
}
template <typename K, typename D>
void RB<K, D>::insert(const K& key, const D& data)
{
_insert(root, key, data);
root->color = BLACK; // 루트는 항상 블랙
}
template <typename K, typename D>
void RB<K, D>::_insert(Node*& node, const K& key, const D& data)
{
if (!node) {
node = new Node(key, data, RED, 1);
return;
}
else if (node->key == key) {
Node* tmp = node;
Node* n = new Node(node->key, data, node->color, node->size);
n->left = node->left;
n->right = node->right;
node = n;
delete tmp;
return;
}
else if (node->key < key) {
_insert(node->right, key, data);
}
else { //node->key > key
_insert(node->left, key, data);
}
if (_isRed(node->right) && !_isRed(node->left)) _rotateLeft(node);
if (_isRed(node->left) && _isRed(node->left->left)) _rotateRight(node);
if (_isRed(node->left) && _isRed(node->right)) _colorFlip(node);
node->size = 1 + _size(node->left) + _size(node->right);
}
template <typename K, typename D>
void RB<K, D>::_rotateRight(Node*& node)
{
Node* tmp = node->left;
node->left = tmp->right;
tmp->right = node;
tmp->color = node->color;
node->color = RED;
tmp->size = node->size;
node->size = 1 + _size(node->left) + _size(node->right);
node = tmp;
}
template <typename K, typename D>
void RB<K, D>::_rotateLeft(Node*& node)
{
Node* tmp = node->right;
node->right = tmp->left;
tmp->left = node;
tmp->color = node->color;
node->color = RED;
tmp->size = node->size;
node->size = 1 + _size(node->left) + _size(node->right);
node = tmp;
}
template <typename K, typename D>
void RB<K, D>::_colorFlip(Node*& node)
{
node->color = _colorChange(node->color);
node->left->color = _colorChange(node->left->color);
node->right->color = _colorChange(node->right->color);
}
template <typename K, typename D>
typename RB<K, D>::Color RB<K, D>::_colorChange(Color c)
{
return c == BLACK ? RED : BLACK;
}삭제 - 어렵다.
공통적으로 가장 인기있는 방식은 부모 포인터를 기반으로 둔다. 이는 상당한 오버헤드를 가지고 처리되어야할 것들이 줄어주지 않는다.
LLRB 2-3 트리에 관한 delete() 함수는 탑다운 2-3-4 트리에서 삽입 연산에 사용된 접근 방식의 역을 토대로 둔다. 이는 2-노드에서 탐색이 끝나지 않게 보장하기 위해서 탐색 경로로 내려가면서 회전과 색 변환을 수행한다. 그래서 가장 아래에서 노드를 삭제할 수 있다. 삽입 연산시 재귀 호출에 따라오는colorFlip(), rotateRight()와 rotateLeft()에 사용되는 코드를 공유하기 위해 코드를 _fixUp()함수로 사용. 이 함수덕에 탐색 경로를 따라 내려가면서 나오는 오른쪽의 레드 링크와 균형이 깨진 4-노드들은 그대로 나둘 수 있다. 남겨진 불균형 부분들은 이 함수를 통해 트리를 올라가면서 고쳐질 것이다. 여기서 오른쪽 노드가 4-노드일때 추가 회전이 요구된다.
// 삽입에서 사용하던 코드를 함수로 만들어 사용
template <typename K, typename D>
void RB<K, D>::_fixUp(Node*& node)
{
if (!node) return ;
if (_isRed(node->right) && !_isRed(node->left))
_rotateLeft(node);
if (_isRed(node->left) && _isRed(node->left->left))
_rotateRight(node);
if (_isRed(node->left) && _isRed(node->right))
_colorFlip(node);
node->size = 1 + _size(node->left) + _size(node->right);
}
// 삽입 코드는 아래와 같이 된다.
template <typename K, typename D>
void RB<K, D>::_insert(Node*& node, const K& key, const D& data)
{
if (!node) {
node = new Node(key, data, RED, 1);
return;
}
else if (node->key == key) {
Node* tmp = node;
Node* n = new Node(node->key, data, node->color, node->size);
n->left = node->left;
n->right = node->right;
node = n;
delete tmp;
return;
}
else if (node->key < key) {
_insert(node->right, key, data);
}
else { //node->key > key
_insert(node->left, key, data);
}
_fixUp(node);
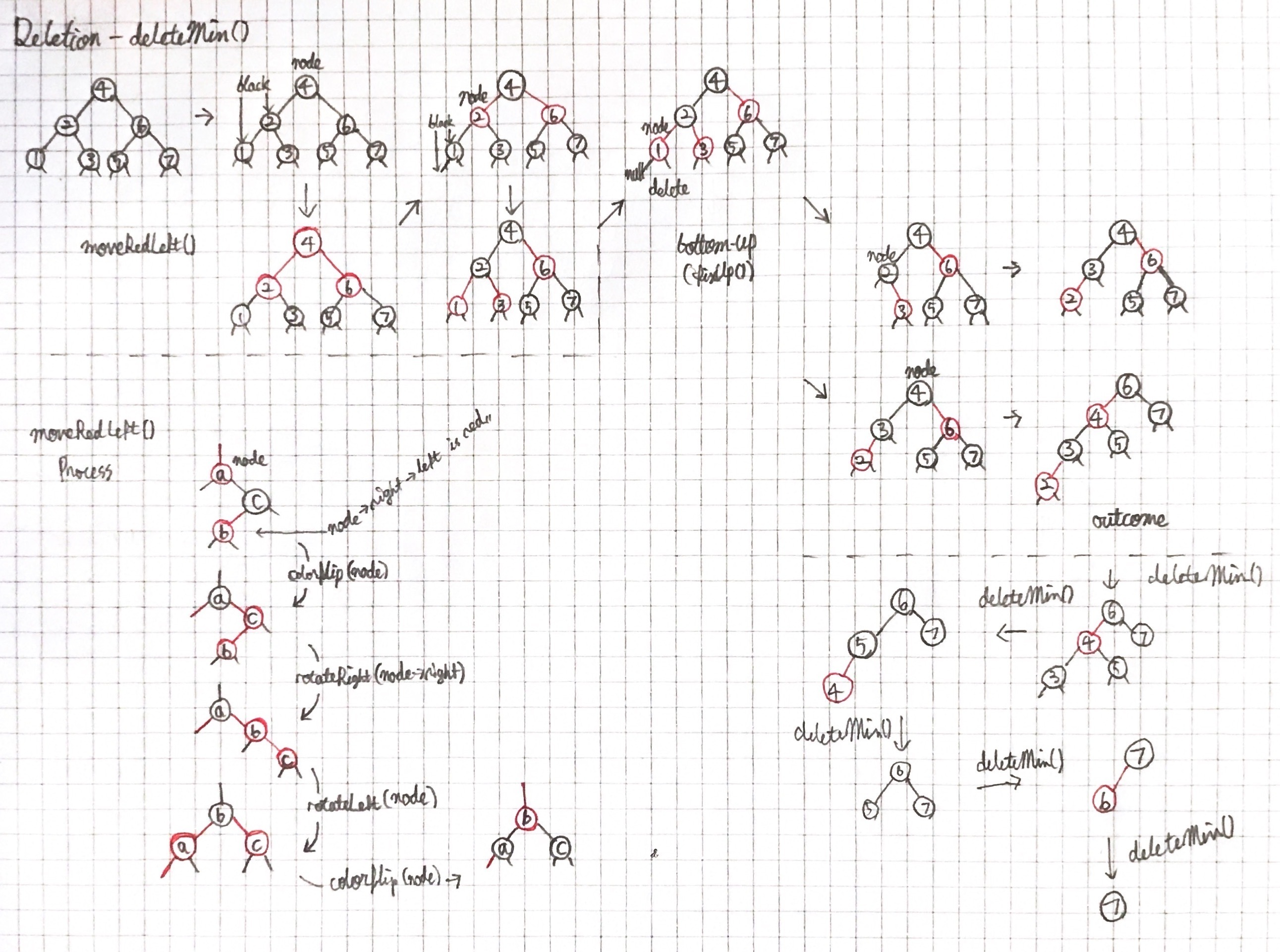
}먼저 웜업으로 deletion-the-minimum 연산을 고려해보면, 균형을 유지하면서 좌측 최하단의 노드를 삭제하는 것이 목적이다. 그렇게 하기 위해서 현재 노드나 그 노드의 왼쪽 자식이 레드인 것을 변하지 않게 유지한다. 현재 노드가 레드이고 그 노드의 왼쪽 자식과 왼쪽의 손자 노드 모두 블랙이 아닌 경우가 아니라면 왼쪽으로 이동함으로서 연산 수행할 수 있다. 이런 경우 colorFlip으로 트리가 변하지 않게 유지할 수 있지만 오른쪽으로 레드 링크로 이어진 노드를 맞이할 수 있다. 이 경우엔 두 회전과 colorFlip으로 교정할 수 있다. 이러한 연산들은 moveRedLeft에서 구현된다.
template <typename K, typename D>
void RB<K, D>::deleteMin()
{
_deleteMin(root);
root->color = BLACK;
}
template <typename K, typename D>
void RB<K, D>::_deleteMin(Node*& node)
{
if (!node->left) {
delete node;
node = nullptr;
return;
}
if (!_isRed(node->left) && !_isRed(node->left->left))
_moveRedLeft(node);
_deleteMin(node->left);
_fixUp(node);
}
template <typename K, typename D>
void RB<K, D>::_moveRedLeft(Node*& node)
{
_colorFlip(node);
if (_isRed(node->right->left))
{
_rotateRight(node->right);
_rotateLeft(node);
_colorFlip(node);
}
}
template <typename K, typename D>
void RB<K, D>::deleteMax()
{
_deleteMax(root);
root->color = BLACK;
}
template <typename K, typename D>
void RB<K, D>::_deleteMax(Node*& node)
{
if (_isRed(node->left))
rotateRight(node);
if (!node->right)
{
delete node;
node = nullptr;
return;
}
if (!_isRed(node->right) && !_isRed(node->right->left))
_moveRedRight(node);
_deleteMax(node->right);
_fixUp(node);
}
template <typename K, typename D>
void RB<K, D>::_moveRedRight(Node*& node)
{
_colorFlip(node);
if (_isRed(node->left->left))
{
_rotateRight(node);
_colorFlip(node);
}
}
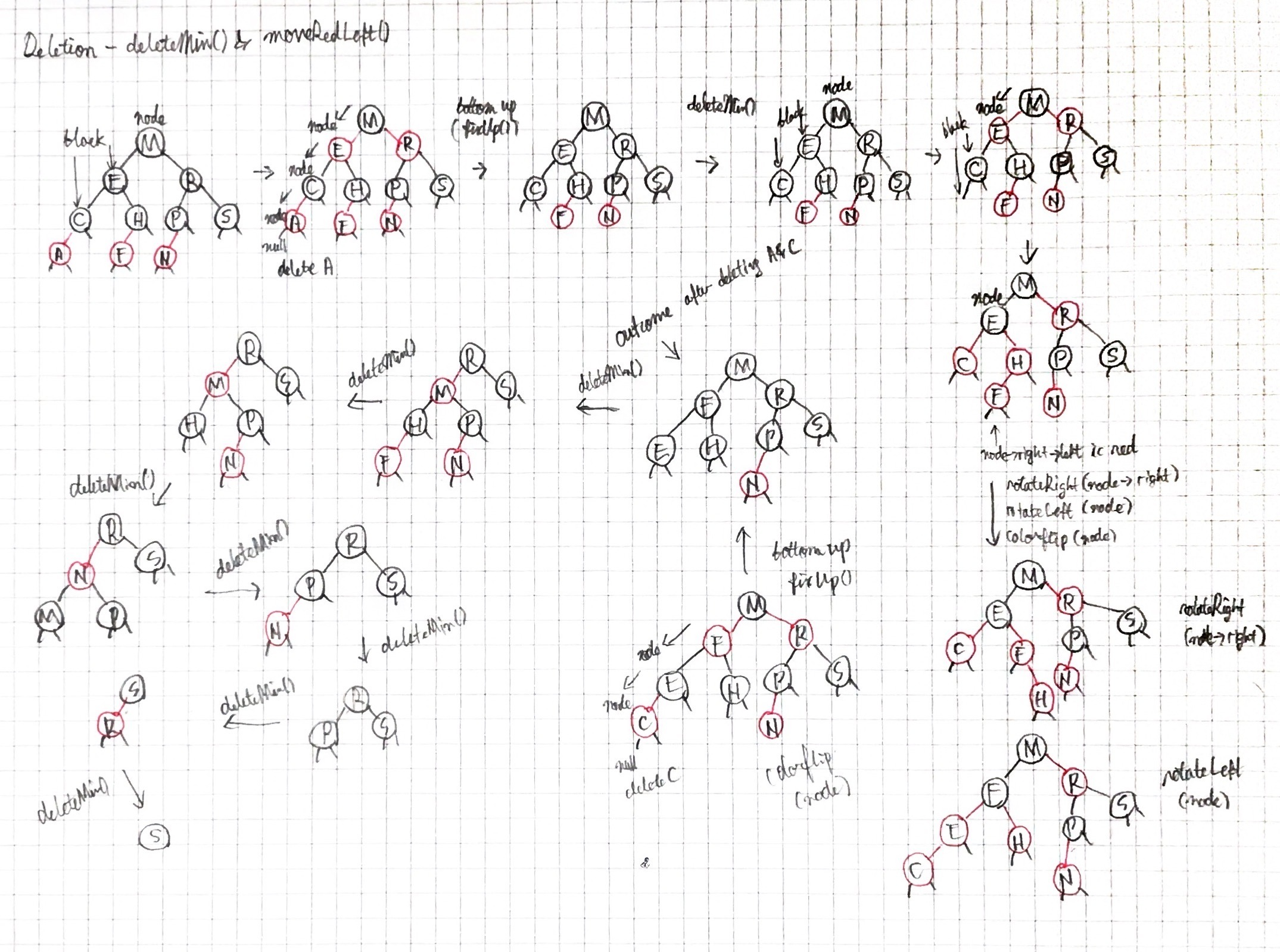
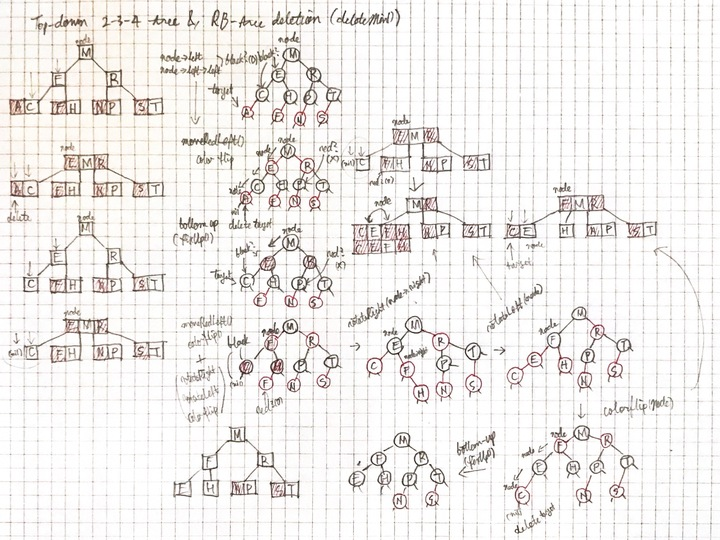
앞서 말했듯이 Top-down 2-3-4트리로 조건에 맞게 3, 4-노드로 변환하면서 경로로 내려온다. 삭제 후 재귀적으로 fixUp() 호출하여 규칙에 맞게 다시 갖춰진다.deleteMin()과 deleteMax()를 잘 보고 그려보면 된다.
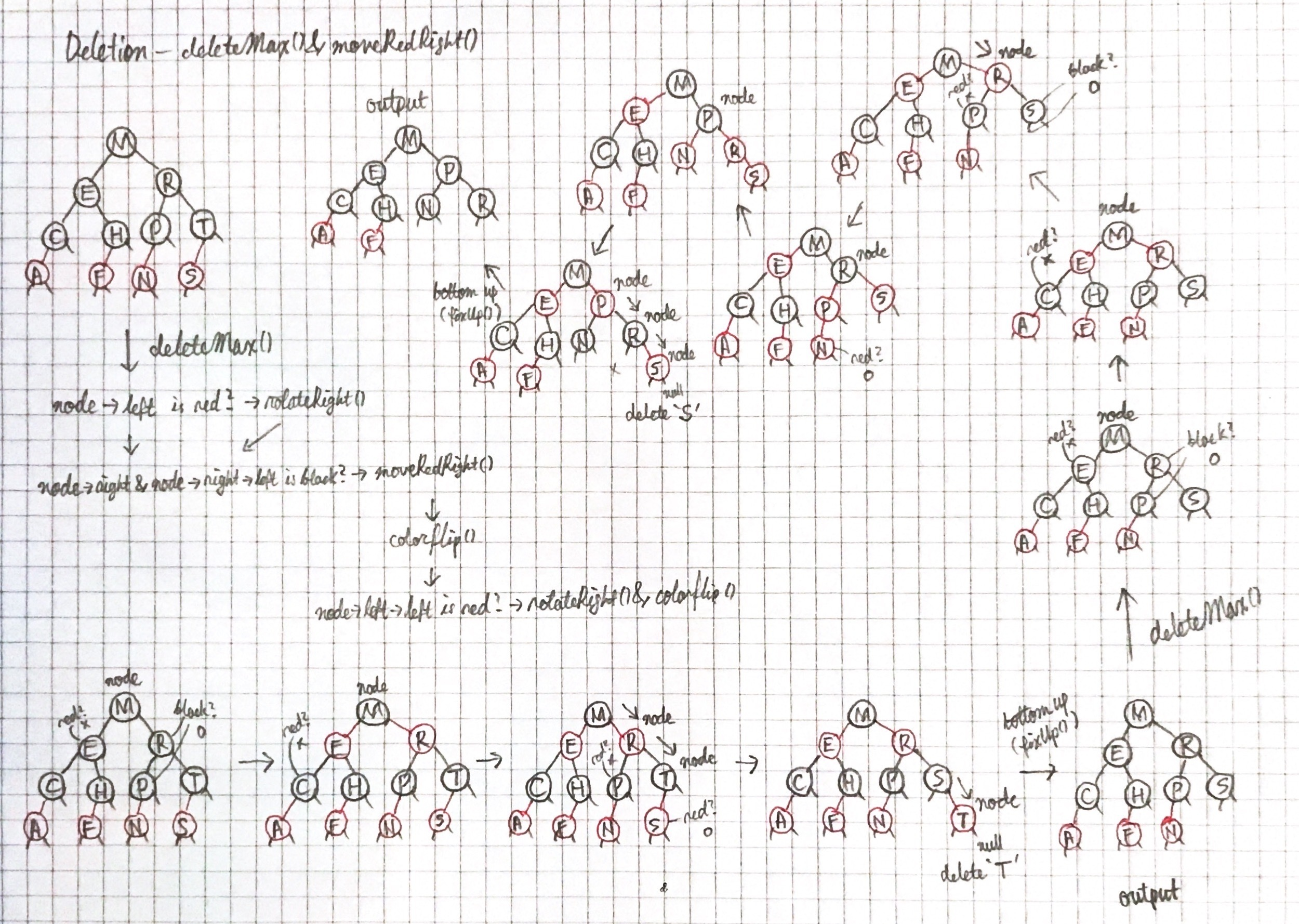
일반적인 삭제는 moveRedRight가 필요. deleteMax()에서 사용해봤다. 이 함수는 moveRedLeft()와 유사하지만 더 간단하다. 트리를 불변하게 유지 시키기 위해서 왼쪽의 레드 링크를 탐색경로에서 오른쪽으로 회전시켜야한다. 만약 internal 노드를 삭제할 때 오른쪽 서브트리에서의 최소 노드와 값과 데이터를 바꾸고 그 최소노드를 삭제한다.
template <typename K, typename D>
void RB<K, D>::_remove(Node*& node, const K& key)
{
if (key < node->key) { // when the search path is towards the left sub-tree of the node, similar to deleteMin()
if (!_isRed(node->left) && !_isRed(node->left->left))
_moveRedLeft(node);
_remove(node->left, key);
}
else { // when the search path is towards the right sub-tree of the node, similar to deleteMax() and when it finds the target
if (_isRed(node->left)) _rotateRight(node);
// when found the key and its right-sub-tree doesn't exist
if (key == node->key && node->right == nullptr) {
delete node;
node = nullptr;
return;
}
if (!_isRed(node->right) && !_isRed(node->right->left))
_moveRedRight(node);
if (key == node->key) {
Node* tmp = _min(node->right);
Node* replace = new Node(tmp->key, tmp->data, node->color, node->size);
replace->left = node->left;
replace->right = node->right;
tmp = node;
node = replace;
delete tmp;
_deleteMin(node->right);
}
else
_remove(node->right, key);
}
_fixUp(node);
}- 출처 : 홍정모의 알고리듬 압축코스 part 1 & https://sedgewick.io/wp-content/themes/sedgewick/papers/2008LLRB.pdf
Dictionary, AVL and Red-Black tree 코드 : https://github.com/kkj-100-010-110/tree
B-Tree
디스크 드라이브나 직접 접근 기억 장치들(direct-access secondary storage devices) 잘 작동하기 위해 디자인된 균형 이진 탐색 트리이다. 레드 블랙 트리와 비슷하지만 B-tree는 디스크 접근 연산들을 최소화 부분에서 더 낫다. 많은 데이터 베이스에서 이 트리를 사용한다.
B-tree 노드는 다양한 노드 수를 가질 수 있다. B-tree의 ‘branching factor’는 꽤 클 수 있다. 다만, 이 크기는 사용되는 디스크 드라이브에 의존적. log의 밑은 높이를 나타내는데 branching factor가 커질 수록 이 높이는 매우 낮아진다.
B-tree는 자연스럽게 이진 탐색 트리를 일반화한 것.
- Data structure on secondary storage
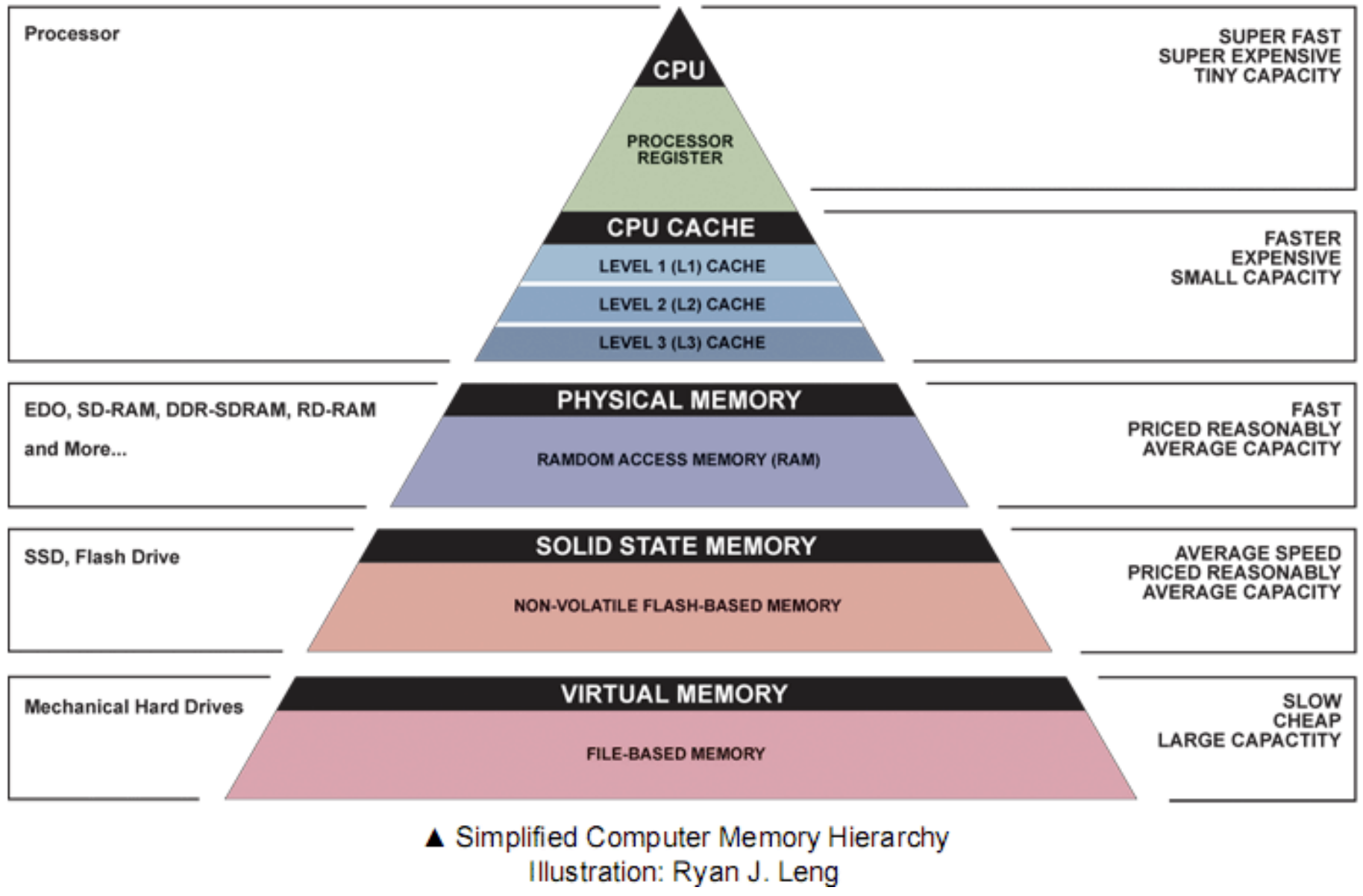
컴퓨터는 메모리 용량을 제공하는데 다양한 기술들을 이용. 메인 메모리는 실리콘 칩으로 구성되어있고 이는 테이프나 디스크 드라이브 같은 자기 저장 기계(magnetic storage technology)보다 빠르고 비싸다. 대부분의 컴퓨터는 solid-state drives(SSD)나 magnetic disk drive 형태의 secondary storage를 가진다. 상대적으로 느리지만 많은 데이터를 저장할 수 있다.
드라이버 구성
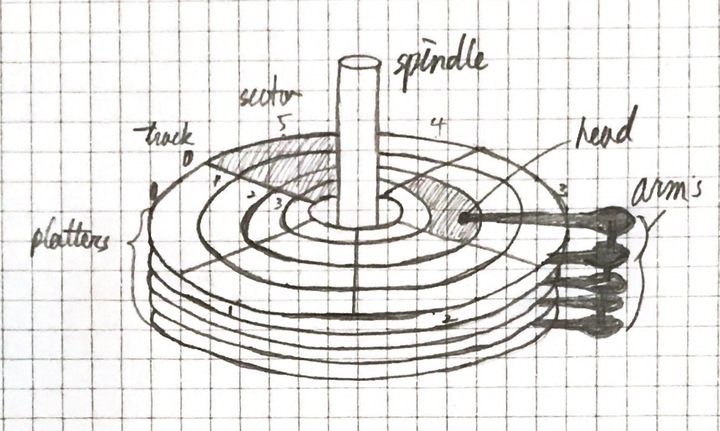
디스크 드라이브는 기계 부품을 움직여야 하므로 굉장히 느리다. 두 부품의 움직임이 있는데 이는 platter들의 회전과 arm들의 움직임이다. 회전의 속도는 분당 5,400-15,000 회전(RPM, revolution per minute)을 가진다. 일반적으로 서버 등급의 드라이브들은 15,000 RPM, 데스크탑 7,200 RPM, 랩탑 5,400 PRM을 가진다. 7,200 RPM은 빨라 보이지만 한번의 회전이 8.33 ms가 소요. 이는 메인 메모리에서 일반적으로 데이터 접근 시간 50 ns 보다 다섯자리 차이 난다. 다른 말로, 컴퓨터가 특정 아이템으로 read/write head에 위치하기 위한 full rotation을 대기하면, 그시간 동안 컴퓨터는 100,000 번 메인 메모리에 접근할 수 있다. 평균 wait 대기하는데 반만 회전하는데 이 또한 메모리 접근 시간에 비하면 굉장히 차이가 크다. arm들의 움직임도 시간이 조금 걸린다. 평균 4 ms 소요.
기계 움직임에 대기하는데 소요되는 시간(latency)를 줄이기 위해서 디스크 드라이브들은 하나의 아이템이 아닌 여러개의 아이템에 한번에 접근한다. 정보(information)는 많은 track 내부에서 연속적으로 나타나는 bit들의 동일한 크기의 block들로 나누어지고, 각 디스크가 읽고 쓰는데 하나 이상의 블록들을 가진다. 전형적인 디스크 블록 사이즈는 512 - 4096 bytes 크기. read/write head가 정확하게 위치해 있고 platter가 원하는 block의 시작점에 회전했을때 자기 저장 디스크 드라이브를 읽고 쓰는 것은 완전한 전자활동을 하며 큰 데이터의 양을 디스크 드라이브는 빠르게 읽고 쓸 수 있다.
종종 디스크 드라이브로부터 정보의 블록에 접근하고 읽는 것이 읽은 모든 정보들을 처리하는 시간보다 더 걸린다. 실행 시간의 두 가지 주요한 요소들은
- 디스크 접근의 수(the number of disk accesses)
- CPU 시간
디스크 접근 수를 디스크 드라이브에 쓰거나 그것으로부터 읽어오는데 필요한 정보의 block 수로 측정. 디스크 접근 시간은 상수가 아님에도(현재 track과 요구되는 track 사이의 거리에 의존적이며, platter의 초기 회전하는 지점에 또한 의존적), 읽고 쓰여진 block의 수는 디스크 드라이브에 접근하는데 사용된 전체 시간의 괜찮은 1차 근사값(first-order approximation)을 제공한다.
전형적인 B-tree 응용에서 처리되는 데이터의 양은 모든 데이터가 메인 메모리에 한번에 알맞게 들어맞을 수 없을 정도로 크다. B-tree 알고리듬은 필요에 따라 디스크로부터 선택된 blocks을 메인 메모리에 복사하고 변경된 block들을 다시 디스크에 쓴다(write). B-tree 알고리듬은 언제든 메인 메모리에 일정한 크기의 block들을 유지하고 메인 메모리의 크기는 B-tree의 크기를 제한하지 않는다.
B-tree의 절차(procedure)는 디스크로부터 정보를 메인 메모리로 읽어(read)올 수 있어야하고 메인 메모리에서 정보를 디스크로 쓸(write) 수 있어야한다. 오브젝트 x가 있다고 가정. x가 현재 메인 메모리에 있다면, 코드는 x의 어트리뷰트들을 참조할 수 있다. 그렇지만 x가 디스크 드라이브에 있다면, 프로시져는 오브젝트 x를 가지고 있는 block을 메인 메모리로 읽기 위해서 x의 어트리뷰트들을 참조하기전에 DISK-READ(x)를 실행시켜야한다.(만약 x가 메인 메모리에 있으면 DISK-READ(x)는 disk accesss를 필요로 하지 않는다. 이를 ‘no-op’이라 한다.) 유사하게 오브젝트 x 어트리뷰트 변경된 내용들을 저장하고 담고 있는 block을 디스크에 쓰기(write) 위해 DISK-WRITE(x)를 호출한다.
x = a pointer to some object
DISK-READ(x)
operations that access and/or modify the attributes of x
DISK-WRITE(x) // omitted if no attributes of x were changed
operations that access but do not modify the attributes of x 컴퓨터는 항상 오직 제한된 수의 block들을 메인 메모리에 유지할 수 있다. B-tree 알고리듬은 컴퓨터가 자동으로 더이상 사용하지 않는 block들을 메인 메모리로부터 보내는(flush) 것을 가정한다.
대부분 B-tree 알고리듬의 실행 시간은 DISK-READ와 DISK-WRITE 연산 수에 달려있다. 이 연산들 각각 가능한 많은 정보를 read 또는 write 하기 원한다. 그래서 B-tree의 노드는 보통 전체 디스크 block의 크기 만큼 크고 이 크기는 B-tree가 가질 수 있는 자식의 수를 제한한다.
디스크 드라이브에 저장된 사이즈가 큰 B-tree는 block의 크기에 비례한 key의 크기에 따라 종종 50-2,000 branching factor를 가진다. branching factor가 크다면 트리의 높이와 키를 찾는 디스크 접근의 수도 현저히 줄어든다. branching factor가 1001이고 height가 2인 트리는 키를 10억개 이상 저장할 수 있다. 만약 루트노드가 영구적으로 메인 메모리에 유지되면 트리에서 키를 찾는 경우 많아봐야 2번의 디스크 접근이면 충분하다.
출처 - Introduction Algorithms
참고 자료 https://www.cs.cornell.edu/courses/cs312/2004sp/lectures/lec24.html
- B-tree 특징 - (출처: 유튜브 - 쉬운코드)
- 각 노드의 최대 자식 수를 M이라하면 각 노드의 최대 키의 수는 M-1이다.
- 루트와 리프 노드를 제외한 각 노드의 최소 자식 수는 (무조건 올림, e.g. M이 3이라면 2)
- 루트 노드를 제외한 각 노드의 최소 키의 수는. - 1
- internal 노드의 키의 수가 x개라면 자녀 노드의 수는 x+1개이다.
- 몇 차 B-tree인지 상관없이 internal 노드는 최소한 2개의 자식 노드를 가진다.
- M이 정해지면 internal 노드들은 최소 개의 자식 노드를 가진다.
- B-tree 특징 - (출처: geeksforgeeks)
- 모든 리프 노드들은 같은 레벨이다.
- 최소 차수 ‘t’에 의해 정의, ‘t’의 값은 disk block 크기에 의존적
- 루트 노드를 제외한 모든 노드들은 최소 t-1 키들을 가져야한다. 루트 노드는 최소한 하나의 키를 가지고 있다.
- 루트를 포함한 모든 노드들은 최대 2*t-1 키들을 가질 수 있다.
- 한 노드의 자식 수는 그 노드의 키 수에 1 더한 값과 동일
- 한 노드의 모든 키는 오름차순으로 정렬되어있다. 두 키 k1과 k2 사이의 자식은 k1에서 k2까지의 범위에서 모든 키를 가질 수 있다.
- 이진 탐색 트리와 달리 루트로 부터 커지거나 줄어든다.
- 다른 균형 이진 탐색 트리들과 같이 탐색, 삽입, 삭제 연산에서 시간복잡도는 O(log n)
- 삽입은 항상 리프 노드에서 발생
https://www.cs.usfca.edu/~galles/visualization/BTree.html
