[211116] 프로그래머스 - 다리를 지나는 트럭

일치하기만 할 뿐, 더 나은 답이 아닙니다.

---

[프로그래머스 - 다리를 지나는 트럭]

알고 가기

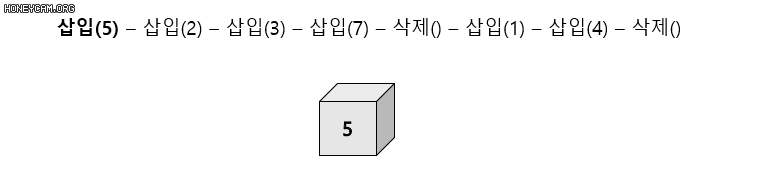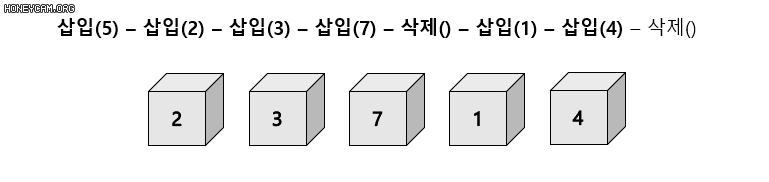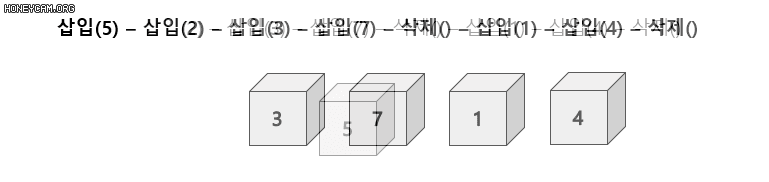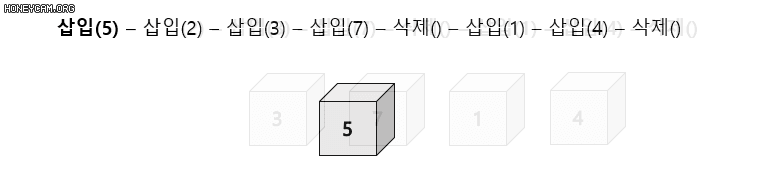
1-1. 스택

• 나중에 들어 온 데이터가 먼저 나가는 후입선출(LIFO)의 자료구조

• 들어오는 곳과 나가는 곳이 동일한 형태
  

1-2. 스택 구현

2-1. 큐

• 먼저 들어온 데이터가 먼저 나가는 선입선출(FIFO)의 자료구조
• 들어오는 곳과 나가는 곳이 모두 뚫려있는 터널과 같은 형태
  

2-2. 큐 구현

2-3. list vs Queue vs deque

	list	Queue	deque
목표	범용성 큰 배열 자료구조	멀티 스레드 환경에서 안전한 자원 교환을 위한 단방향 큐	doubly-ended-queue list 보다 빠르게 동작하는 양뱡향 큐
구현	queue = []	from queue import Queue queue = Queue()	from collections import deque queue = deque()
장점	n번째 요소 바로 접근 가능	삽입/삭제 후, shitf 없음	양뱡향에서 삭제/삽입 가능, 스택으로 사용 가능
단점	삭제/삽입을 끝내고 연관된 요소를 한 칸씩 shift	유연한 연산 힘듬	linked list n번째 요소 접근에 힘듬

2-4. 시간복잡도 비교

import time
import sys, collections

L = []
for i in range(1, 60000000):
    L.append(i)
dq = collections.deque(L)

start_time1 = time.time()
d1 = L[30000000]  # list 접근
print(time.time() - start_time1)  # 0.0

start_time2 = time.time()
d2 = dq[30000000]  # deque 접근
print(time.time() - start_time2)  # 0.037924766540527344

start_time3 = time.time()
L.insert(0,10)  # list 삽입
print(time.time() - start_time3)  # 0.060869693756103516

start_time4 = time.time()
dq.appendleft(10)   # deque 삽입
print(time.time() - start_time4)  # 0.0

문제

일차선 다리를 트럭 여러 대가 지나가고자 한다

다리 길이, 다리가 견딜 수 있는 무게, 트럭 배열이 주어질 때

모든 트럭이 다리를 건너려면 필요한 최소 시간을 구하시오

조건

• 다리에는 최대 bridge_lentgh 대 올라갈 수 있음
• weigth 이하 무게를 견딜 수 있음
• 다리에 완전히 오르지 않은 트럭은 무시

ex

최대 2대 올라갈 수 있음

무게를 10 까지 견딜 수 있음

무게가 [7, 4, 5, 6] 순서대로 다리를 지날 예정

경과 시간	다리를 지난 트럭	다리를 건너는 트럭	대기하는 트럭
0		[ - - ]	7,4,5,6
1		[ - 7 ]	4,5,6
2		[ 7 - ]	4,5,6
3	7	[ - 4 ]	5,6
4	7	[4 5]	6
5	7,4	[ 5 - ]	6
6	7,4,5	[ - 6]
7	7,4,5	[ 6 - ]
8	7,4,5,6	[ - - ]

나의 풀이

def solution(bridge_length, weight, truck_weights):
   sec = 0	# 경과시간
   bridge = [0] * bridge_length	# 다리 위 트럭 배열
   while bridge:		# 다리 위에 트럭이 모두 지나갈 동안
       bridge.pop(0)		# 가장 앞의 트럭 탈출
       if truck_weights:	# 대기하는 트럭이 존재한다면
	   # 다리 위 트럭의 무게 + 앞으로 진입할 트럭의 무게 <= 다리가 견딜 수 있는 무게
           if sum(bridge) + truck_weights[0] <= weight:
               bridge.append(truck_weights.pop(0)) # 대기하는 트럭 순서대로 삽입
           else: 		# 다리가 견딜 수 없다면
               bridge.append(0) # 다리 길이 유지를 위해 삽입
        sec += 1 		# 시간 증가
   return sec

더 나은 풀이

from collections import deque

def solution(bridge_length, weight, truck_weights):
   sec = 0
   bridge = deque([0] * bridge_length)
   truck = deque(truck_weights)	# 트럭 배열도 deque
   current_weights = 0		# 현재 다리 위 무게
   while bridge:
       current_weights -= bridge.popleft() # 탈출하는 트럭은 무게에서 제외
       if truck:
           if current_weights + truck[0] <= weight:
               in_truck = truck.popleft()
               bridge.append(in_truck)
               current_weights += in_truck # 진입하는 트럭은 무게에 추가
           else:
               bridge.append(0)
       sec += 1
   return sec