[211222] 프로그래머스 - 배달

일치하기만 할 뿐, 더 나은 답이 아닙니다.

---

[프로그래머스 - 배달]

알고가기

1. 최단 경로 문제

• n 지점 -> m 지점
• n 지점 -> 모든 지점
• 모든 지점 -> 모든 지점

각 지점은 노드, 지점 간 경로는 간선

2. 다익스트라 알고리즘

매 상황에서 가장 비용이 적은 노드를 선택해 임의의 과정을 반복하는 알고리즘

조건

• n 지점 -> 모든 지점
• 음의 간선 비용 X

성능

• 모든 노드를 선형 탐색 -> O(N²)
• 노드 수가 비약적으로 많아지면, heap을 활용해야 함

과정

1. 출발 노드 설정

2. 최단 거리 테이블 초기화

3. 방문하지 않은 노드 중에서 최단거리가 가장 짧은 노드 선택

4. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신

5. 3, 4 반복

3. heap

우선순위 큐(Priority Queue) : 가장 우선순위가 높은 데이터 추출

우선순위 큐의 시간복잡도 : logN
각 노드마다 이웃한 노드의 최단거리를 갱신 => 최대 인접 노드 E

O(E logN)

문제

N 개의 마을이 존재하고 이웃한 마을은 양뱡향으로 통행할 수 있습니다.

1번 마을에서 k 시간 이하 소요되는 마을만 음식 배달이 가능하다고 할 때, 음식 배달이 가능한 마을의 수를 구하시오.

조건

• 1 ≤ N ≤ 50
• 마을 간 통행 정보가 담긴 배열 road 는 2000개 이하의 정보를 담을 수 있음
• 마을 간 도로는 여러 개 존재할 수 있음

ex

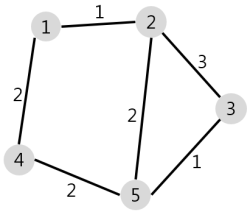
마을 수	마을 간 통행 정보	배달 최소 시간
5	[[1,2,1],[2,3,3],[5,2,2],[1,4,2],[5,3,1],[5,4,2]]	3

나의 풀이

from collections import defaultdict 
import heapq 

def solution(N, road, K): 
   answer = 0 
   graph = defaultdict(list) 
   for start, end, time in road:
       graph[start].append((end, time)) 
       graph[end].append((start, time))
   #	1: [(2, 1), (4, 2)], 
   #	2: [(1, 1), (3, 3), (5, 2)],
   #	3: [(2, 3), (5, 1)],
   #	4: [(1, 2), (5, 2)],
   #	5: [(2, 2), (3, 1), (4, 2)]
   
   Q = [(0, 1)] # 1번 마을부터 해당 마을 까지 시간, 마을번호
   dist = defaultdict(int) 
   while Q:
       time, node = heapq.heappop(Q)
       # 방문하지 않은 마을인지
       if node not in dist: 
           dist[node] = time 
           for end, time2 in graph[node]:
               # 지금 까지 걸린 시간 + end 로 갈 경우 걸릴 시간
               tmp = time + time2 
               heapq.heappush(Q, (tmp, end)) 
               
   for key in dist: 
       if dist[key] <= K: 
           answer += 1 
           
   return answer

Q	dist
[(0, 1)]	{}
[(1, 2), (2, 4)]	{1:0}
[(2, 1), (2, 4), (3, 5), (4, 3)]	{1: 0, 2: 1}
[(2, 4), (3, 5), (4, 3)]	{1: 0, 2: 1}
[(3, 5), (4, 1), (4, 3), (4, 5)]	{1: 0, 2: 1, 3: 4}