Word Vectors

How to Represent Word?

'의미' 의 정의부터 살펴보자.

- the idea the is represented by a word, phrase, etc. 
- the idea thaat a person wants to express by using words, signs, etc. 
- the idea that is expressed in a work of writing, art, etc. 

언어학적으로 보통 '의미'(meaning)는 signifier (symbol), signified (idea or thing), 또는 denotational semantic 으로 생각된다.

이런 '의미'가 있는 단어를 어떻게 표현할 수 있을까? 흔히 사용하는 방법은 WordNet 이다. 이는

• 단어의 synonym 과 hypernyms 를 사용해서 dictionary 를 구성한다.
• 단어에 대한 어느정도 의미를 제공하지만 다양한 nuance를 놓칠 수 있다.
• 또한 새로 생기는 단어, slang 을 놓치기 쉽다.
• human labor 로 사람이 직접 만든다. = 비용이 든다.
• 정확한 word similarity를 계산하기 어렵다.

One-hot Vector

과거의 NLP 에서는 단어를 discrete symbol로 여기고, 단어를 다음과 같이 one-hot vector로 표현했다. one-hot vector는 단어를 뜻하는 것 하나만 1, 나머지는 0으로 표현한 vector로, vector size는 vocab size와 같다.

motel = [0 0 0 0 0 0 0 0 0 1 0 0 0 0]
hotel = [0 0 0 0 0 0 1 0 0 0 0 0 0 0]

이러한 표현 방법의 문제점은 비슷한 의미의 단어더라도 완전히 다르게 표현된다 는 것이다. motel과 hotel은 비슷하지만 두 vector가 서로 otrhogonal (독립적) 이기 때문에 one-hot vector의 similarity 를 찾기 어렵다. 또한 단어가 많아지면 벡터의 크기가 매우 커진다.

이런 similarity 문제를 해결하기 위해 WordNet의 synonym(동의어) list를 만드는 방법도 있지만, incompleteness 문제, 방대한 테이블 크기 문제 등의 이유로 사용하기 어렵다. 대신에 vector 에 similarity 를 encode 하도록 하는 방법이 있다. 이러한 단어 벡터 표현을 word embedding 또는 word representation 이라고 한다.

Word Vector

단어의 의미는 그 주변에 자주 나타나는 단어에 의해 주어진다. (= distributional semantics) 어떤 단어 w가 text에 나타날 때, context는 그 주변에 나타나는 단어들의 집합이라고 할 수 있다. 따라서 비슷한 context에 있는 단어는 유사할 것이다. 이러한 사실로부터 각 단어들을 dense vector로 만든다. one-hot vector와 달리 단어의 의미를 여러 차원에 분산시킨다. word vector는 word embedding, word representation, distributed representation, distributed word representation 이라고도 표현한다.

banking = [0.286 0.792 -0.1777 -0.107 0.109 -0.542 0.271]

Word2Vec Algorithm

Word2Vec 은 word vector 를 학습하는 framework 이다. large corpus of text 를 가지고 있을 때 fixed vocabulary 의 모든 단어를 vector로 표현하자. 그리고 test의 각 position t 를 center word c와 context word (outside word) o 로 표현을 해보자. $P(o|c)$ 또는 $P(c|o)$ 를 계산하기 위해서 word vectors의 similarity를 사용한다. 이 probability를 최대화 하도록 word vector를 계속해서 조정한다.

각 position에 대해서, center word $w_j$가 주어질 때, fixed window size m 내의 context word 를 예측하는 것이다.

$Likelihood = L(\theta) = -\frac{1}{T} \prod^T_{t=1} \prod_{-m\leq j \leq m,j\neq0}log P(w_{t+j}|w_t;\theta)$

Objective function (cost function or loss function) $J(\theta)$ 는 다음과 같이 negative log likelihood 를 사용한다.

$J(\theta) = -\frac{1}{T}logL(\theta) = -\frac{1}{T}\sum^T_{t=1} \sum_{-m\leq j \leq m,j\neq0} logP(w_{t+j}|w_t;\theta)$

Objective function $J(\theta)$ 를 최소화하는 것이 예측 성능을 최대화한다. 그럼 여기서 $J(\theta)$를 최소화 하고 싶은데, $P(w_{t+j}|w_t;\theta)$는 어떻게 계산할 수 있을까?

word w 에 대해서 두가지 vector 를 사용할 것이다. 하나는 $v_w$ 로 w 가 center word 인 vector, 다른 하나는 $u_w$ 로 w 가 context word인 vector 이다. 그러면 center word c 와 context word o 에 대해서 다음 식을 쓸 수 있다.

$P(o|c) = \frac{\exp(u^T_ov_c)}{\sum_{w V} \exp(u^T_wv_c)}$

• 이 식에서 $\exp$ 를 쓰는 것은 확률이 negative 가 되는 것을 방지하기 위함이다.
• $u^T_ov_c$ 에서의 dot product는 o와 c의 similarity를 비교하기 위함이다. 값이 클수록 유사하다.
• $\sum_{w V} exp(u^T_wv_c)$ 는 probability distribution을 만들기 위해 전체 vocab 으로 normalize 해주는 것이다. 최종적으로 모든 단어의 확률의 합은 1이 될 수 있도록 한다.

Training a model

model을 학습하기 위해서 loss를 최소화하도록 파라미터를 조정해야 한다. 모델을 훈련시키기 위해서 모든 vector gradient를 계산해야 한다. 모든 단어들은 두개의 vector ($v_w, u_w$) 를 가지고 있다. 이 모든 파라미터들을 gradient로 최적화 할 것이다.

** context vector, outside vector 각각에 대해 gradient 구하는 과정 과제 참고

Model variants

1. Skip-grams (SG): 모든 외부 단어로 가운데 단어를 예측하는 방식
2. Continuous Bag of Words (CBOW): 가운데 1개의 단어로 외부의 모든 단어를 예측하는 방식

Optimization

Gradient Descent

Gradient Descent 는 cost function $J(\theta)$ 를 최소화하는 알고리즘이다. 손실 함수의 gradient(기울기)를 계산해서, gradient의 반대 방향으로 조금씩 이동하게 된다.

• Update equation (in matrix notation):
  $\theta^{new} = \theta^{old} - \alpha\nabla_\theta J(\theta)$

  $\alpha$ = step size or learning rate

• Update equation (for single parameter):
  $\theta^{new}_j = \theta^{old}_j - \alpha\frac{\partial}{\partial\theta^{old}_j} J(\theta)$

• Algorithm

while True: 
	theta_grad = evaluate_gradient(J,corpus,theta)
    theta = theta - alpha * theta_grad

Stochastic Gradient Descent

corpus 의 모든 단어에 대해 $J(\theta)$의 gradient 를 계산하면 전체 파라미터에 대해 계산하기 때문에 비용이 너무 크다는 문제가 있다. 하나를 update를 하려는데 아주 긴 시간을 기다려야 할 수 있다. 그래서 사용하는 방법이 Stochastic Gradient Descent (SGD) 이다. 전체 corpus에 대해 gradient 하는게 아니라 하나의 center word 또는 batch 에 대해 하는 방법이다. 반복해서 window를 sample 하고, 각각에 대해 update 한다. (cf. mini-batch update)
여러개의 sample을 모아서 mini-batch 라고 부른다. 보통 32개, 64개의 sample로 구성된다. 여러개의 sample을 사용하기 때문에 noise가 줄어들고 병렬화가 가능하다는 장점이 있다. 또한 빠른 학습이 가능하다.

• Algorithm

while True: 
	window = sample_window(corpus)
    theta_grad = evaluate_gradient(J,window,theta)
    theta = theta - alpha * theta_grad

SGD with word vectors

각 window에 대해서 gradient를 반복한다. 하지만 각 window마다, 기껏해야 2m+1 단어를 갖기 때문에 $\nabla_\theta J_t(\theta)$ 는 상당히 sparse 하다는 문제가 있다. 실제로 나타나는 단어에 대해서만 word vector를 업데이트하게 될 것이다.
이런 문제를 해결하가 위한 방법으로 word vector에 대한 Hash를 들고 다니는 방법이 있다.

Word2vec

Skip-gram model with nagative sampling

Skip-gram 은 center word 한 개로 주변 단어들을 예측하는 방법이다. 이전까지 써오던 probability notation인
$P(o|c) = \frac{\exp(u^T_ov_c)}{\sum_{w V} \exp(u^T_wv_c)}$
는 계산하는데 비용이 많이 든다는 게 단점이다. 그래서 standard word2vec 대신 skip-gram model with negative sampling 을 생각해보자는 것이다.
핵심 아이디어는 True pair (center word와 context window 내의 단어) 와 Noise pair (center word와 임의의 단어) 에 대해 binary logistic regression 훈련을 하자는 것이다.
objective function은 다음과 같다.
$J(\theta) = \frac{1}{T}\sum^T_{t=1}J_t(\theta)$

이렇게 하는 목적은 context window 내의 단어들이 center word 가까이에서 나타날 확률은 maximize 하고, random word 가까이 나타날 확률은 minimize 하는 것이다.

But why not capture co-occurence counts directly?

co-occurrence matrix X 를 구성할 수 있는 두가지 옵션이 있다.

1. Window 의 관점
   Word2Vec과 비슷하다. 각 단어 주변에 window를 사용해서 syntactic, semantic 정보를 둘 다 뽑아낸다.

2. Full document 의 관점
   Latent Semantic Analysis 를 가능하게 하는 general topic들을 준다.

window-based co-occurence matrix 의 예시로 window size = 1 이라 가정하고 symmetric하다고 생각하자. 다음의 예시 문장들의 co-occurence matrix 는 다음과 같다.

• I like deep learning.
• I like NLP.
• I enjoy flying.
  

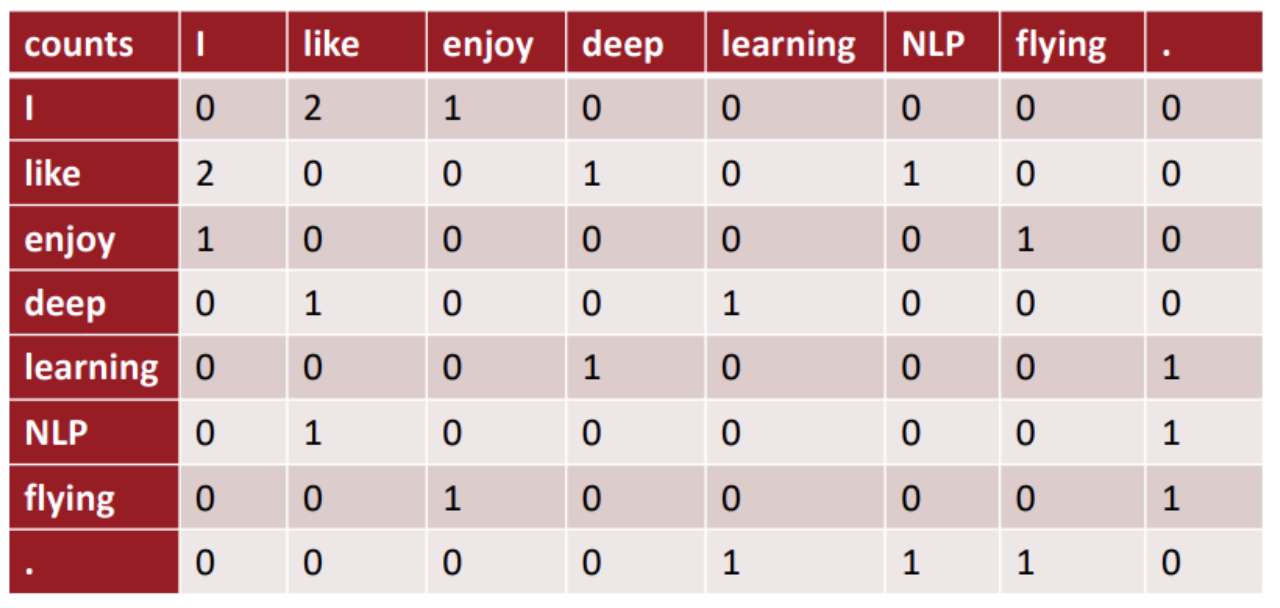
하지만, (1) 단어의 크기가 증가하면 이렇게 사용하기 어렵다. (2) 상당히 high dimensional 해서 많은 저장공간이 필요하다. (3) 이후의 분류 모델들은 sparsity 문제가 생긴다. 즉 모델이 robust 하지 않다.

Low dimensional vectors

그래서 해결책으로 low dimensional vector 를 사용해보자. 아이디어는 가장 중요한 정보들을 fixed size의 작은 dimension으로, dense vector 로 만들자는 것이다. 보통 25-1000 dimension으로 word2vec 과 비슷하다. 그럼 차원을 어떻게 줄일 수 있을까?

[방법]

• Singular Value Decomposition (SVD) 를 사용한다.

  • Full SVD 에서 (1) 필요없는 항들을 없애 차원을 줄인 후, (2) 가장 작은 singular value를 버린다.

  • word vectors in Python

    import numpy as np 
    la = np.linalg
    words = ["I", "like", "enjoy", "deep", "learning", "NLP", "flying", "."]
    X = np.array([[0, 2, 1, 0, 0, 0, 0, 0],
              	  [2, 0, 0, 1, 0, 1, 0, 0],
              	  [1, 0, 0, 0, 0, 0, 1, 0],
              	  [0, 1, 0, 0, 1, 0, 0, 0],
              	  [0, 0, 0, 1, 0, 0, 0, 1],
              	  [0, 1, 0, 0, 0, 0, 0, 1], 
              	  [0, 0, 1, 0, 0, 0, 0, 1],
              	  [0, 0, 0, 0, 1, 1, 1, 0]])
    U, s, Vh = la.svd(X, full_matrices=False)
    

    for i in xrange(len(words)):
    	plt.text(U[i,0], U[i,1], words[i]) 

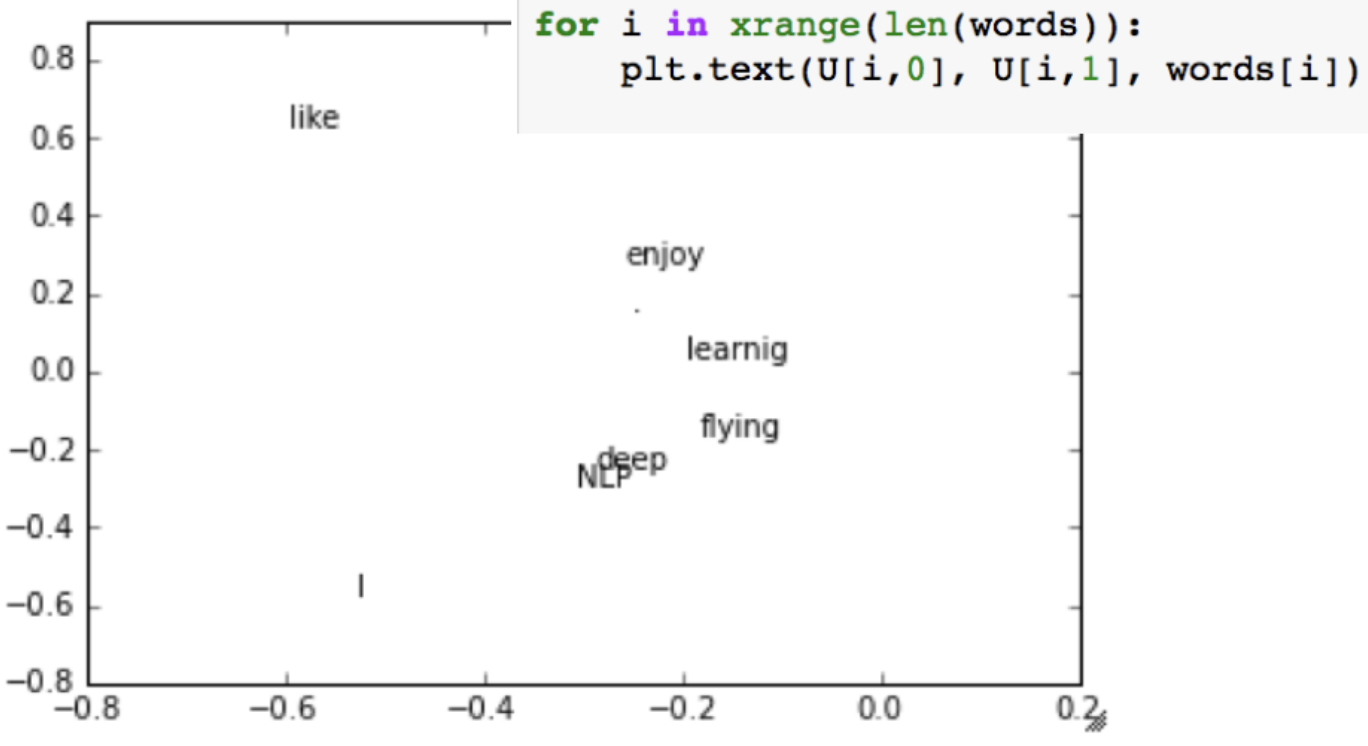
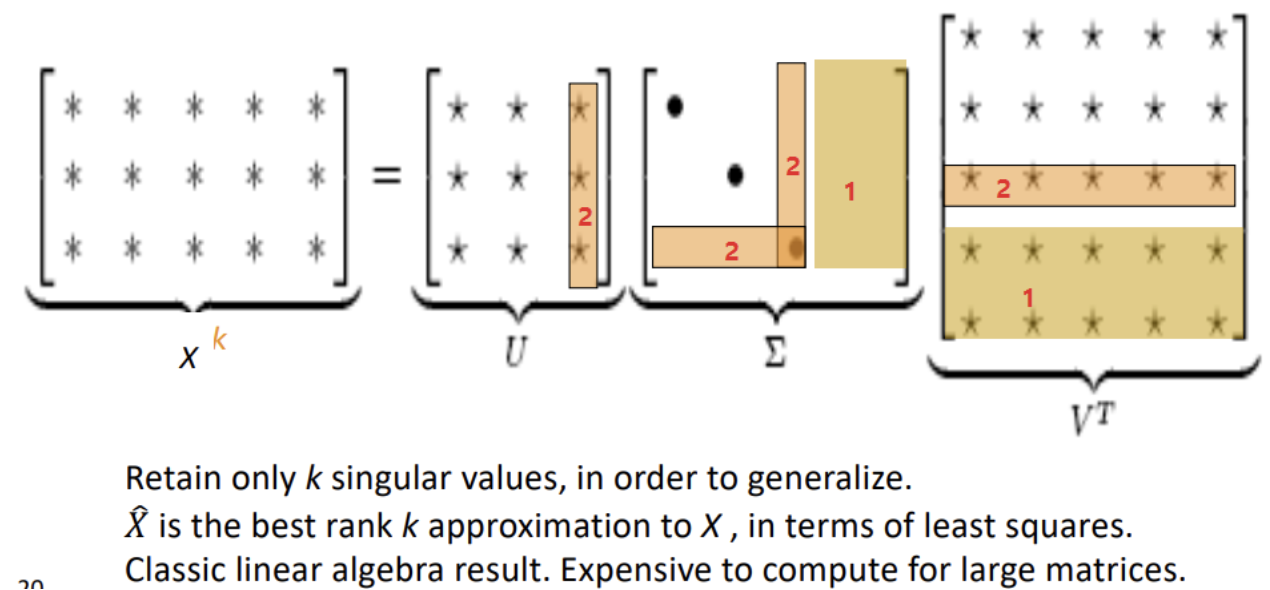
Hacks to X

• Count를 scaling 해주는 것은 많이 도움이 될 수 있다.
  • the, he, has와 같은 function word 들은 상당히 자주 쓰이는데, 이러면 이 syntax들이 너무 큰 영향을 받게 된다.
  • 이럴 때는, raw count를 그대로 사용하는 대신에, 이렇게 자주 출현하는 단어들에 대한 전처리를 해주는 것이 필요하다.
  • 예를 들어 더 가까운 단어를 더 많이 계산하는 Ramped windows 를 사용, count 대신에 Pearson correlation을 사용해서 negative 값은 0으로 하는 방법이 있다. 또는 PPMI 를 사용하는 방법도 있다.
  • 이렇게 전처리를 해주고 나면 syntactic 또는 semantic pattern 이 보이는 경우가 있다.

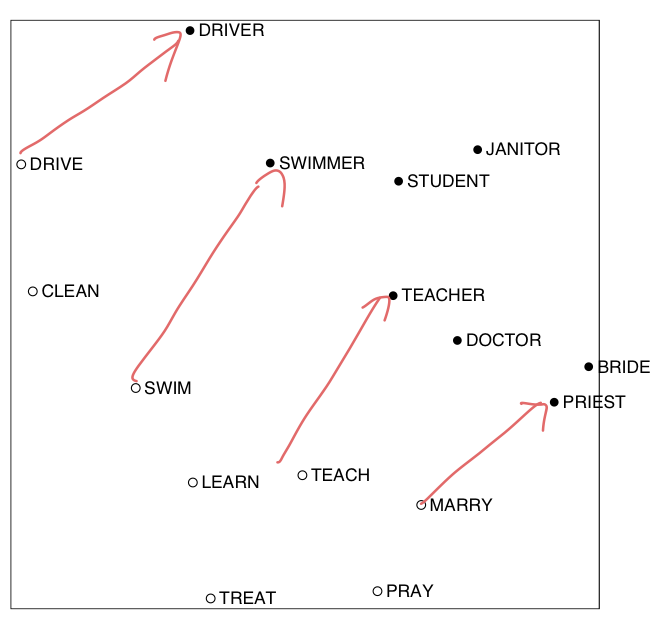
Count based vs. Direct prediction

NLP 의 두가지 큰 방법론이 있다.

• Count based
  • LSA, HAL, COALS, PCA 등
  • Training 속도가 빠르다.
  • 통계 정보를 효율적으로 사용한다.
  • 단어의 유사도를 계산하는데만 사용할 수 있다.
  • 단어 사이의 관계를 확인할 순 없다.
  • 복잡한 패턴을 인식할 수 없다.

• Direct prediction
  • NNLM, HLBL, RNN, Skip-gram/CBOW 등
  • 전체적인 통계 정보를 활용하지 않는다. (window 내의 데이터만 사용하기 때문)
  • 대부분의 영역에서 좋은 성능을 내는 모델 생성할 수 있다.
  • 단어 유사도에 대해 복잡한 패턴도 잡아낼 수 있다.

GloVe

word2vec은 window 내의 정보만 사용한다는 점에서 전체적인 문장에 대한 이해가 떨어진다는 단점이 있다. 그래서 direct prediction 과 count based 방식을 합쳐서 적용해보려는 시도가 있다. 중요한 insight는 co-occurence 확률의 비가 meaning componenet 들을 encode 할 수 있다는 것이다.

count based 방법인 LSA는 DTM이나 TF-IDF 행렬과 같이 각 문서에서의 각 단어의 빈도수를 카운트 한 행렬이라는 전체적인 통계 정보를 입력으로 받아 차원을 축소(Truncated SVD)하여 잠재된 의미를 끌어내는 방법론이다. prediction based 방법인 Word2Vec는 실제값과 예측값에 대한 오차를 손실 함수를 통해 줄여나가며 학습하는 예측 기반의 방법론이다.
LSA 는 카운트 기반으로 코퍼스의 전체적인 통계 정보를 고려하기는 하지만 단어 의미의 유추 작업(Analogy task)에는 성능이 떨어진다. Word2Vec는 예측 기반으로 단어 간 유추 작업에는 LSA보다 뛰어나지만, 임베딩 벡터가 윈도우 크기 내에서만 주변 단어를 고려하기 때문에 코퍼스의 전체적인 통계 정보를 반영하지 못한다. GloVe 는 이러한 기존 방법론들의 각각의 한계를 지적하며, LSA의 메커니즘이었던 카운트 기반의 방법과 Word2Vec의 메커니즘이었던 예측 기반의 방법론 두 가지를 모두 사용한다.

어떻게 word vector space 내에서 co-occurence 확률의 비가 linear 한 meaning components가 되게 할 수 있을까?
=> word vector 들의 내적이 log (co-occurence probability)와 같아지게 정의하면 두 벡터간의 차이를 linear 한 형태로 표기할 수 있다.

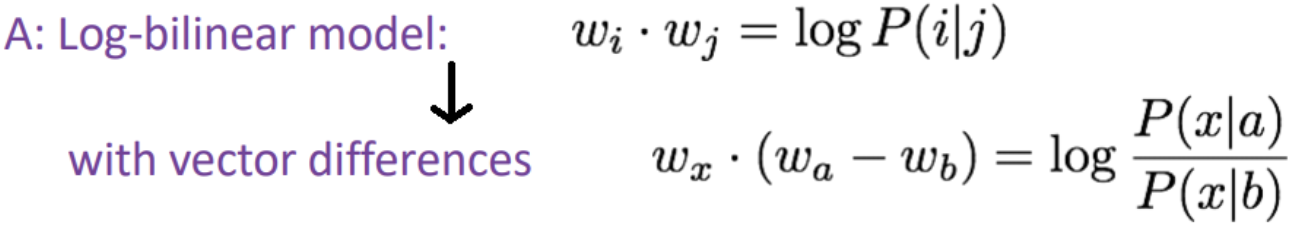
GloVe 모델의 objective function

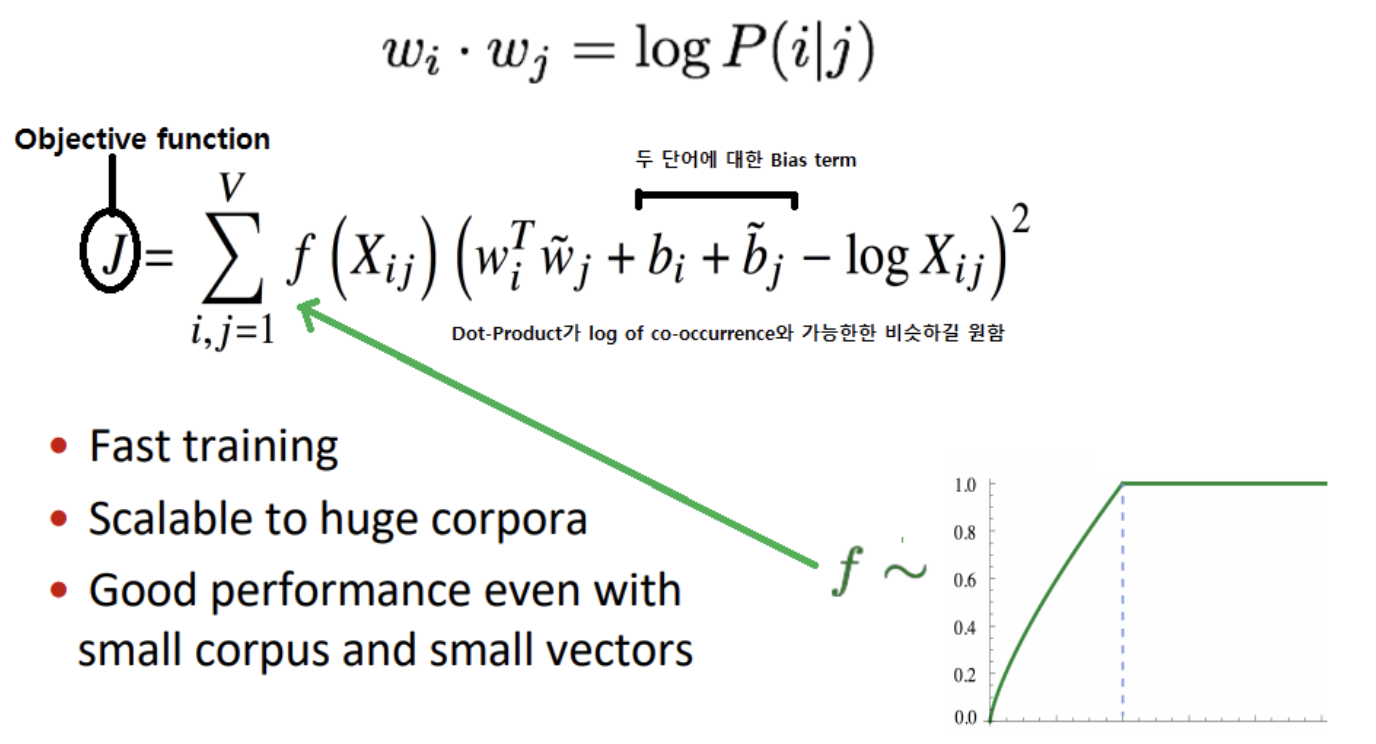
GloVe Results

Word vector evaluation

word vector 를 어떻게 평가할 지에 대한 방법이다.

1. Intrinsic

   • 특정 subtask에 대한 평가
   • 연산이 빠르다.
   • 해당 시스템을 이해하는데 도움을 준다.
   • 실제 task와의 correlation 관계가 확립되지 않았다면 정말 실세계에 도움이 될 지는 명확하지 않다.

2. Extrinsic

   • 실제 task (real task) 상에서의 평가
   • accuracy 계산에 긴 시간이 걸릴 수 있다.
   • subsystem 상에 어떤 문제가 있는지에 대해 명확하게 알 수 없다.
   • 하나의 subsystem을 다른 subsystem으로 교체했는데 정확도가 향상될 수 있다.

Intrinsic word vector evaluation

• Word Vector Analogies
  • Intrinsic Evaluation은 Vector Space addition 이후의 cosine distance가 얼마나 intuitive semantic & syntactic analogy questions를 잘 잡아내는지를 근거로 word vector를 평가

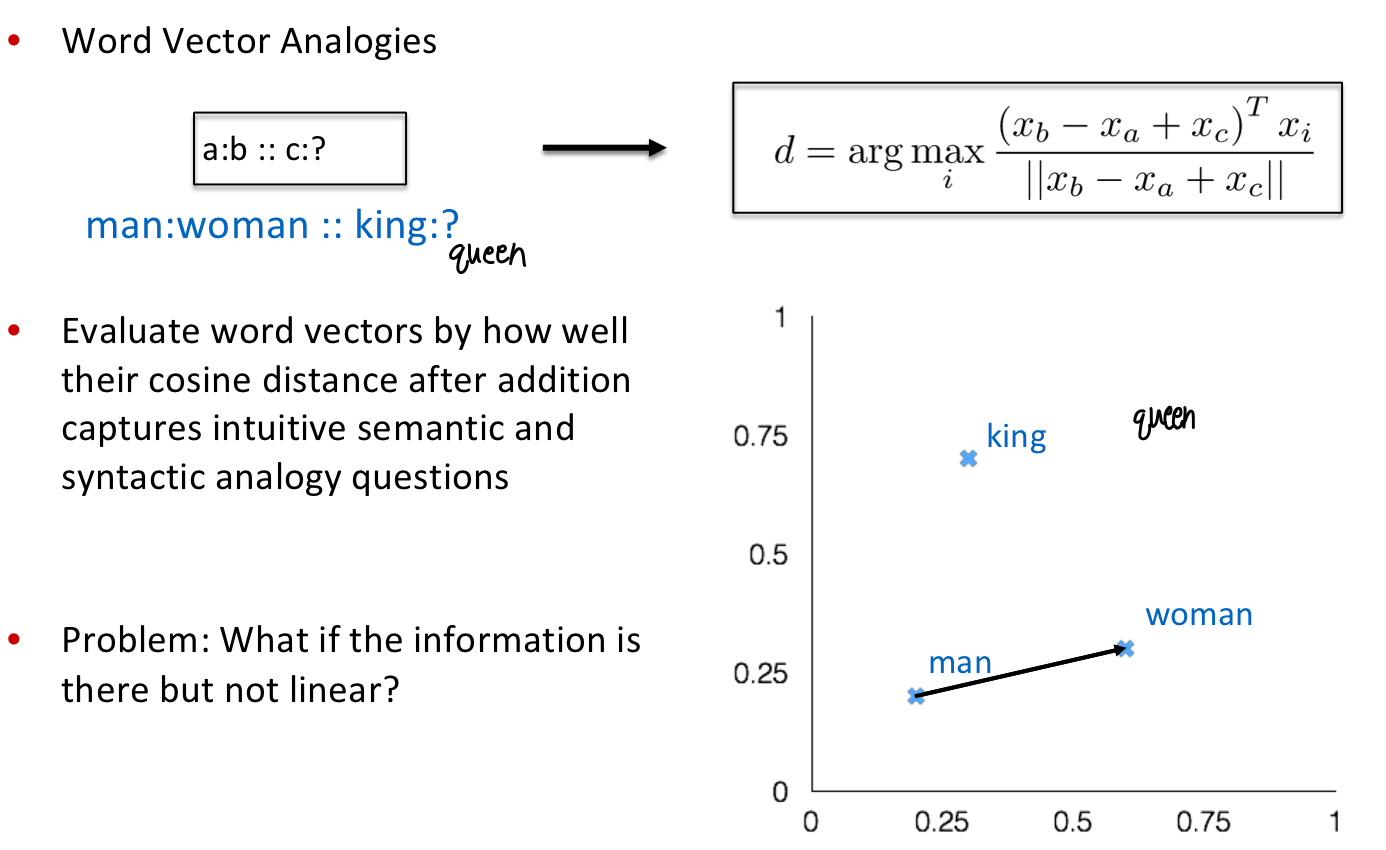
GloVe 모델을 쓰면 Linear 한 property 를 갖고 있는 것을 확인할 수 있다.

Word Ambiguity

많은 단어들은 여러개의 의미를 가지고 있다. 그렇기 때문에 한 단어를 사용해도 다른 의미로 사용되는 경우가 생긴다. 동일한 단어의 서로 다른 의미를 표현하는 방법들이 있다.

Multiple sensors for a word

• 하나의 단어가 벡터 공간에서 서로 다른 cluter를 형성하는 경우, 해당 단어를 여러개로 분류해서 벡터를 생성한다. (ex) $bank_1, bank_2, bank_3, ...$)
• 대부분의 의미를 확장되어서 사용되기 때문에 어느정도 연관이 있다. 때문에 의미를 구분하는 것이 명확하지 않을 수 있다.

Weighted average

• 한 단어의 서로 다른 의미를 나타내는 벡터들에 가중치를 부여해서 weighted verage 를 사용한다.
• 예를 들어 pike 라는 단어에 대해서 $v_{pike_1}, v_{pike_2}, ...$ 의 벡터가 존재한다면 pike 에 대한 최종 벡터 $v_{pike}$ 는 다음과 같이 정의한다.
  • $v_{pike} = \alpha_1 v_{pike_1} + \alpha_2 v_{pike_2} + ... + \alpha_n v_{pike_n}$
  • $\alpha_1 = \frac{f_1}{f_1+f_2+...+f_n}$
• weighted average 를 사용하는 경우 실제로 유의미한 결과를 제공한다.
  • 고차원 영역에서 해당 단어의 각 의미를 나타내는 벡터들을 sparse 하게 표현되기 때문에, 전테 벡터의 일부에 단어의 의미를 나타낼 수 있다.

[Reference]

• Stanford CS224N: Natural Language Processing with Deep Learning - http://web.stanford.edu/class/cs224n/index.html
• https://misconstructed.tistory.com/30
• https://data-weirdo.github.io/data/2020/10/03/data-nlp-02.Wv/
• https://wikidocs.net/22885