[백준] 2225 합분해 [java]

문제

https://www.acmicpc.net/problem/2225

풀이 방법

0부터 n까지 k개를 뽑아 n을 만드는 경우의 수를 구하는 문제이다.
순열을 이용하여 완전탐색으로 풀면 최대 200P200 -> 무조건 시간초과
DP로 해결해야 한다.

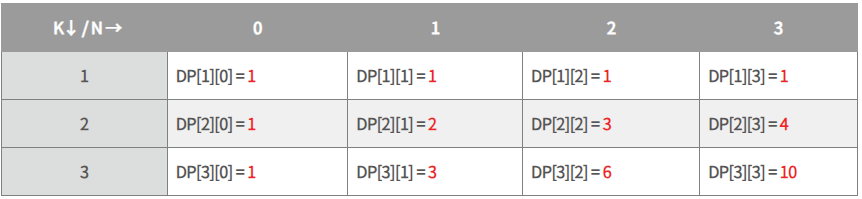
k = 1일 때, 숫자 한개로 수를 만드는 방법은 1개이다.
k = 2일 때, 숫자 한개로 n 이하의 수를 만드는 방법에 1개를 더하면 된다. 무슨소리냐면,
n = 3 / k = 2 일 때,

• 숫자 1개로 0을 만드는 경우 + 3
• 숫자 1개로 1을 만드는 경우 + 2
• 숫자 1개로 2를 만드는 경우 + 1
• 숫자 1개로 3을 만드는 경우 + 0
  ---> 이 모든 경우를 합한 것이 숫자 2개로 3을 만드는 경우의 수이다.
  n = 3 / k = 2 일 때,
• 숫자 2개로 0을 만드는 경우 + 3
• 숫자 2개로 1을 만드는 경우 + 2
• 숫자 2개로 2를 만드는 경우 + 1
• 숫자 2개로 3을 만드는 경우 + 0
  ---> 이 모든 경우를 합한 것이 숫자 2개로 3을 만드는 경우의 수이다.
  
  
  따라서 점화식은 dp[k][n] = dp[k - 1][0] + ... + dp[k - 1][n] 이다

코드

import java.util.Scanner;

// 0부터 20까지 2개를 더해서 20이 되는 경우의 수  /  0부터 6까지 4개를 더해서 6이 되는 경우의 수
// 순열로 풀 수 있지만 시간초과 -> dp로 해결
public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int k = scanner.nextInt();
        int[][] dp = new int[k + 1][n + 1];

        for(int i = 0; i <= n; i++){
            dp[1][i] = 1;
        }

        for(int i = 2; i <= k; i++){
            for(int j = 0; j <= n; j++){
                for(int idx = 0; idx <= j; idx++){
                    dp[i][j] = (dp[i][j] + dp[i - 1][idx]) % 1_000_000_000;
                }
            }
        }

        System.out.println(dp[k][n]);
    }
}