[파이썬/Python] Leet Code 104(Easy): Maximum Depth of Binary Tree

숨·2025년 9월 7일

코테

알고리즘 문제 풀이

목록 보기

128/128

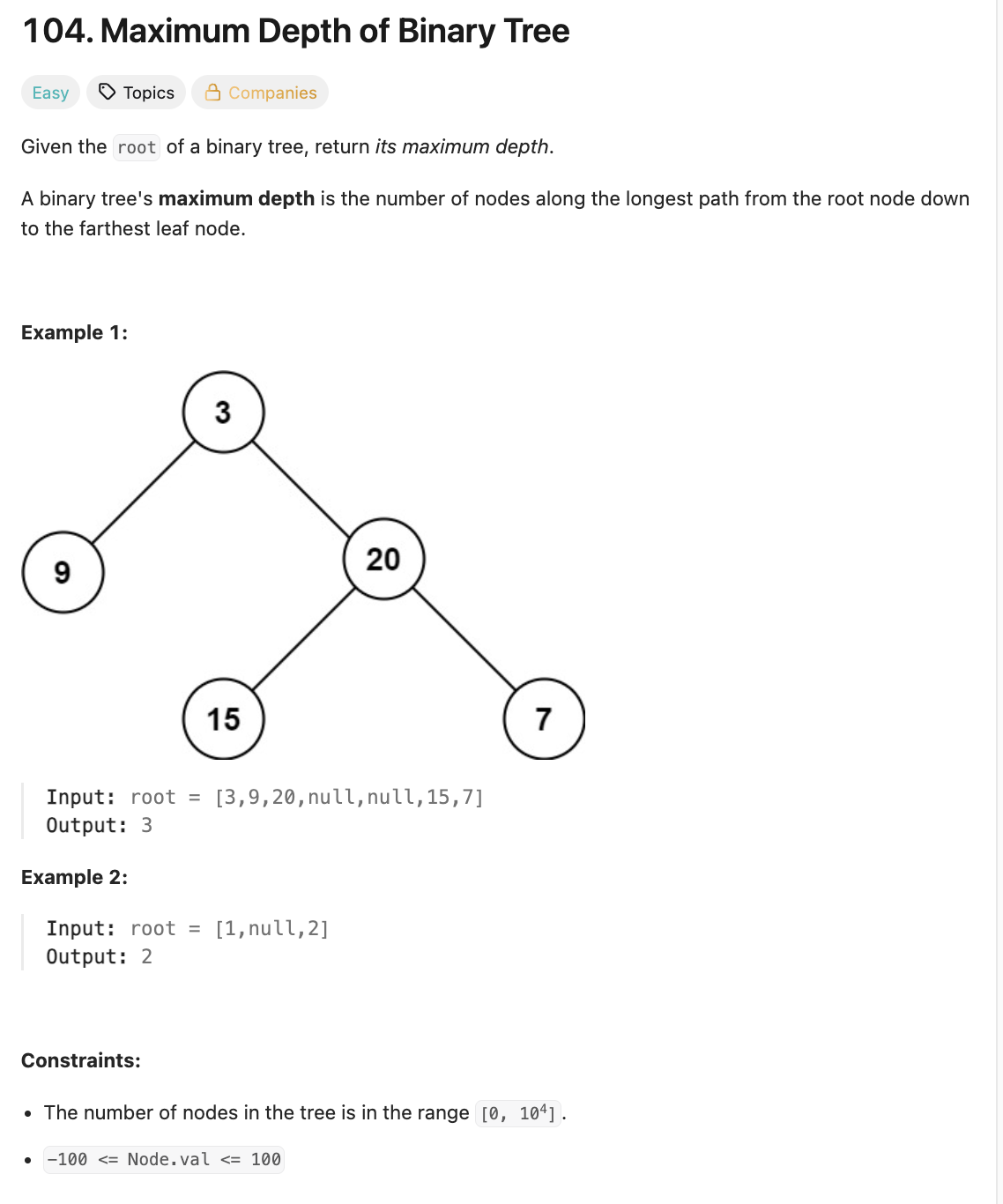
📌 문제 : Leet Code 104

📌 문제 탐색하기

Node.val : 노드의 값 ( $-100 ≤ Node.val ≤ 100$ )
노드 개수 ( $0 ≤ 노드 개수 ≤ 10^4$ )

문제 풀이

이진 트리의 root가 주어졌을 때 최대 깊이를 반환하는 문제이다.

root의 처음 노드부터 끝까지 재귀적으로 더 큰 깊이를 갖도록 움직이며 깊이를 계산하면 된다.

가능한 시간복잡도

DFS로 이진 트리의 모든 노드 방문 → $O(n)$

최종 시간복잡도
최악의 경우에도 $O(n)=O(10^4)$ 이므로 충분히 동작할 수 있다.

알고리즘 선택

재귀적으로 DFS

📌 코드 설계하기

노드 없으면 깊이 0
왼쪽과 오른쪽 중 깊이가 더 큰 값에 +1해 반환 -> DFS를 재귀함수로 구현

📌 시도 회차 수정 사항

📌 정답 코드

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        # 노드 없으면 깊이 0
        if root is None:
            return 0

        # 왼쪽과 오른쪽 중 깊이가 더 큰 값에 +1해 반환 -> DFS를 재귀함수로 구현
        left_depth = self.maxDepth(root.left)
        right_depth = self.maxDepth(root.right)

        return max(left_depth, right_depth) + 1

결과

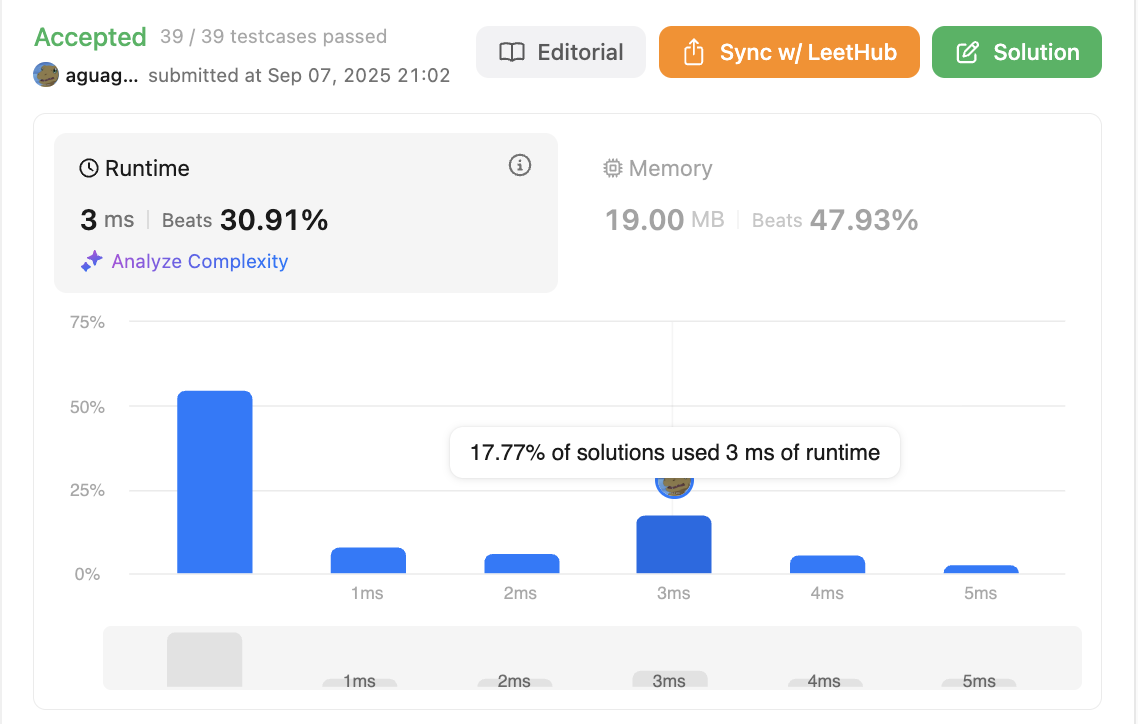
👍 다른 풀이

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

# DFS stack
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
    	# 노드 없으면 깊이 0 반환
        if root is None:
            return 0
            
        # 스택 초기화
        stack = [(root, 1)]
        
        # 최대 깊이 변수 초기화
        max_depth = 0
        
        # 스택에 빌 때까지 반복
        while stack:
        	# 노드, 깊이 pop
            node, depth = stack.pop()
            
            # 깊이가 더 크면 업데이트
            if depth >= max_depth:
                max_depth = depth
            
            # 왼쪽 노드 없으면 현재 왼쪽에서의 깊이 추가
            if node.left is not None:
                stack.append((node.left, depth + 1))
                
            # 오른쪽 노드 없으면 현재 오른쪽에서의 깊이 추가
            if node.right is not None:
                stack.append((node.right, depth + 1))
        
        # 최대 깊이 반환
        return max_depth

Runtime : 0ms
특징
- 스택 + 반복 방식 → 재귀 방식과 달리 최대 재귀 깊이 한계 없이 동작
- 현재 방문 노드 & 그 때 깊이 정보 함께 스택에 저장
- 모든 노드 1번 씩 방문 → 이진 트리 크기만큼의 시간복잡도 $O(n)$

💡 스택 DFS(반복형 DFS)가 재귀 DFS보다 유리한 경우

깊이가 매우 깊을 경우

재귀 호출 스택의 최대 깊이 제한 의한 RecursionError 피할 수 있음

스택 메모리 제어 필요 시

사용자 제어 영역에서 깊이 & 흐름 관리

특정 로직 및 데이터 병렬 처리에 적합

노드와 깊이 외 추가 정보를 함께 스택에 쌓아 처리 가능

동시성 & 비동기 처리 등에서 유연성 높음

인터프리터/언어 제한 환경

재귀 호출 제한 심한 환경에선 반복형 DFS로 구현해야 함

⚠️ 주의

재귀 DFS는 탐색 순서를 그나마 보장

스택 DFS는 탐색 순서 보장이 어렵다

추가 조건 있을 경우 작은 노드를 우선 탐색하도록 처리 필요

✏️ 회고

여전히 클래스 활용이 어렵다. 백준이랑 프로그래머스에서도 DFS/BFS 문제를 풀어서 여러 형식이 주어졌을 때 유동적으로 풀이를 작성할 수 있도록 연습해야 겠다.

숨

이전 포스트