[파이썬/Python] Leet Code 2375. Construct Smallest Number From DI String

숨·2025년 8월 7일

📌 문제 탐색하기

pattern : I, D로 구성된 문자열 ( $1 ≤ pattern의 길이 ≤ 9$ )
num : pattern에 따라 만들어진 정수로 구성된 문자열

문제 풀이

길이 n의 pattern을 입력받아 만들 수 있는 길이 n+1인 문자열 num 중 가장 작은 숫자를 구하는 문제이다.

아래의 조건을 만족하는 사전식 순서에서 가장 작은 문자열 num을 반환한다.

0-indexed string이 만들어지는 조건

num은 정수 1 ~ 9까지의 숫자로 구성되고, 각 숫자는 한번만 사용 가능

I → $num[i] < num[i+1]$

D → $num[i] > num[i+1]$

pattern을 만족하는 모든 경우의 수를 구하고 그 중에 가장 작은 숫자를 찾으면 될 것이라 생각했다.
하지만 pattern의 제약 사항에 따라 시간 초과가 발생할 수 있을 것 같다.
만들면서 현재 가장 작다고 판단한 숫자를 기준으로 커지면 더 찾기 전에 종료하는 방법을 찾아야 할 것이다.
→ 이 때 Backtracking 개념을 떠올렸다.

📖 Backtracking (백트래킹)

해를 찾는 도중 해가 아니어서 막히면 되돌아가서 다시 해를 찾아가는 기법 → 최적화, 결정 문제 해결 방법

모든 가능한 경우의 수 중 특정 조건 만족하는 경우만 확인하는 것

모든 경우의 수 탐색(DFS)하면서 조건문 등으로 답이 될 수 없는 상황 정의해 탐색 중지 & 되돌아가기

일종의 가지치기를 통해 반복 횟수 감소 가능

가지치기를 얼마나 잘하느냐에 따라 효율성 결정

DFS와 BFS

DFS

모든 경우의 수(모든 경로) 탐색해 경우의 수 줄이지 못함

사용 👍 : 모든 경우의 수 고려해야 할 경우 BFS보다 좋음 (큐의 크기 엄청 커지기 때문)

사용 ❌ : 트리 깊이가 무한대가 될 경우

BFS

모든 분기 검색하면서 상태공간 탐색 → 어느 한 부분에서 원하는 해 발견하면 최단 거리가 됨

따라서 이 문제는 DFS로 만들 수 있는 모든 num을 만들면서도, 조건에 맞지 않으면 만드는 것을 멈추는 식으로 구현하면 될 것이다.

가능한 시간복잡도

탐색 깊이 → $O\left(\frac{9!}{(9 - (len(pattern)+1))!}\right)$

최종 시간복잡도
최악의 경우 키의 수는 $O(9!)이 되는데 이는 충분히 수행 가능하다.

알고리즘 선택

DFS로 하면서 백트래킹 적용

📌 코드 설계하기

dfs 구현
1-1. 조건을 만족하는 숫자를 찾았다면 저장
1-2. 1~9까지의 숫자를 활용해 숫자 계속 만들면서 조건 만족하는지 확인
dfs 함수에서 정의한 변수들을 활용해 dfs 수행하고 원하는 형식의 출력 반환

📌 시도 회차 수정 사항

1회차

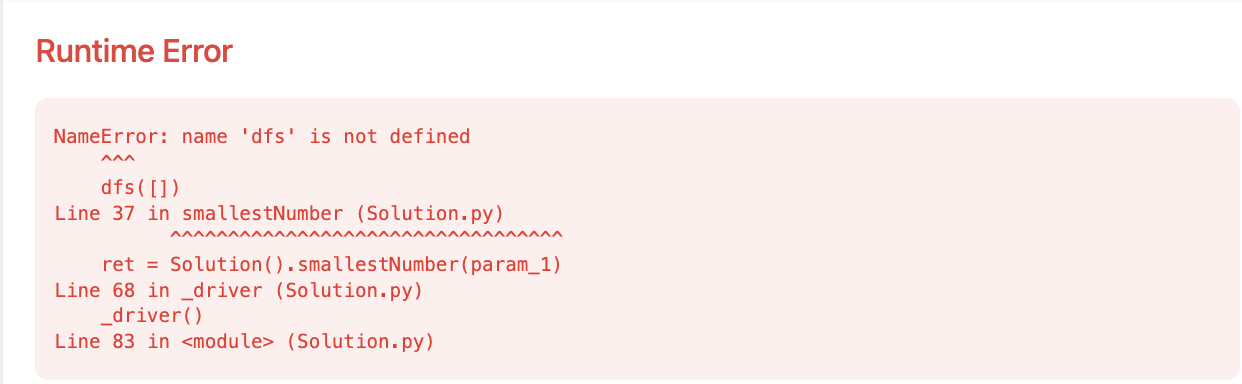
dfs() 함수가 클래스 내부에 정의되어 있지만 메서드처럼 정의 → 인스턴스 메서드에서 호출 불가
내부에서 사용할 변수들은 self.으로 붙여서 클래스 멤버로 선언

📌 정답 코드

class Solution:
    def smallestNumber(self, pattern: str) -> str:
        # 내부에서 사용할 변수들은 self.으로 붙여서 클래스 멤버로 선언
        self.visited = [0] * 10
        self.nums = []
        self.pattern = pattern

        # DFS 호출
        self.dfs([])

        # 첫 번째 결과를 문자열로 변환해서 리턴
        return ''.join(map(str, self.nums[0]))

    def dfs(self, used_digits):
        if len(used_digits) == len(self.pattern) + 1:
            self.nums.append(used_digits)
            return True

        for digit in range(1, 10):
            if self.visited[digit]:
                continue

            if not used_digits or (
                self.pattern[len(used_digits) - 1] == 'I' and used_digits[-1] < digit or
                self.pattern[len(used_digits) - 1] == 'D' and used_digits[-1] > digit
            ):
                self.visited[digit] = 1

                if self.dfs(used_digits + [digit]):
                    return True

                self.visited[digit] = 0

        return False

결과

✏️ 회고

머릿속에 생각한 방식을 코딩하는 것이 어렵다. 바로 코드를 쓰기 보다 어떻게 구현해야할지 잘게 쪼개면서 구현 난이도를 낮출 수 있도록 노력해야 겠다.
DFS 구현하는게 아직 익숙하지 않다. DFS 위주로 문제 풀이를 하되, BFS로도 구현하는 식으로 해봐야 겠다.
백트래킹에 대해서 겁을 먹었었는데 생각보다 이미 많이 활용하는 방식이라는 것을 알았다. 조금 더 적극적으로 관련 문제에 도전해야겠다.