[파이썬/Python] Leet Code 498(Medium): Diagonal Traverse

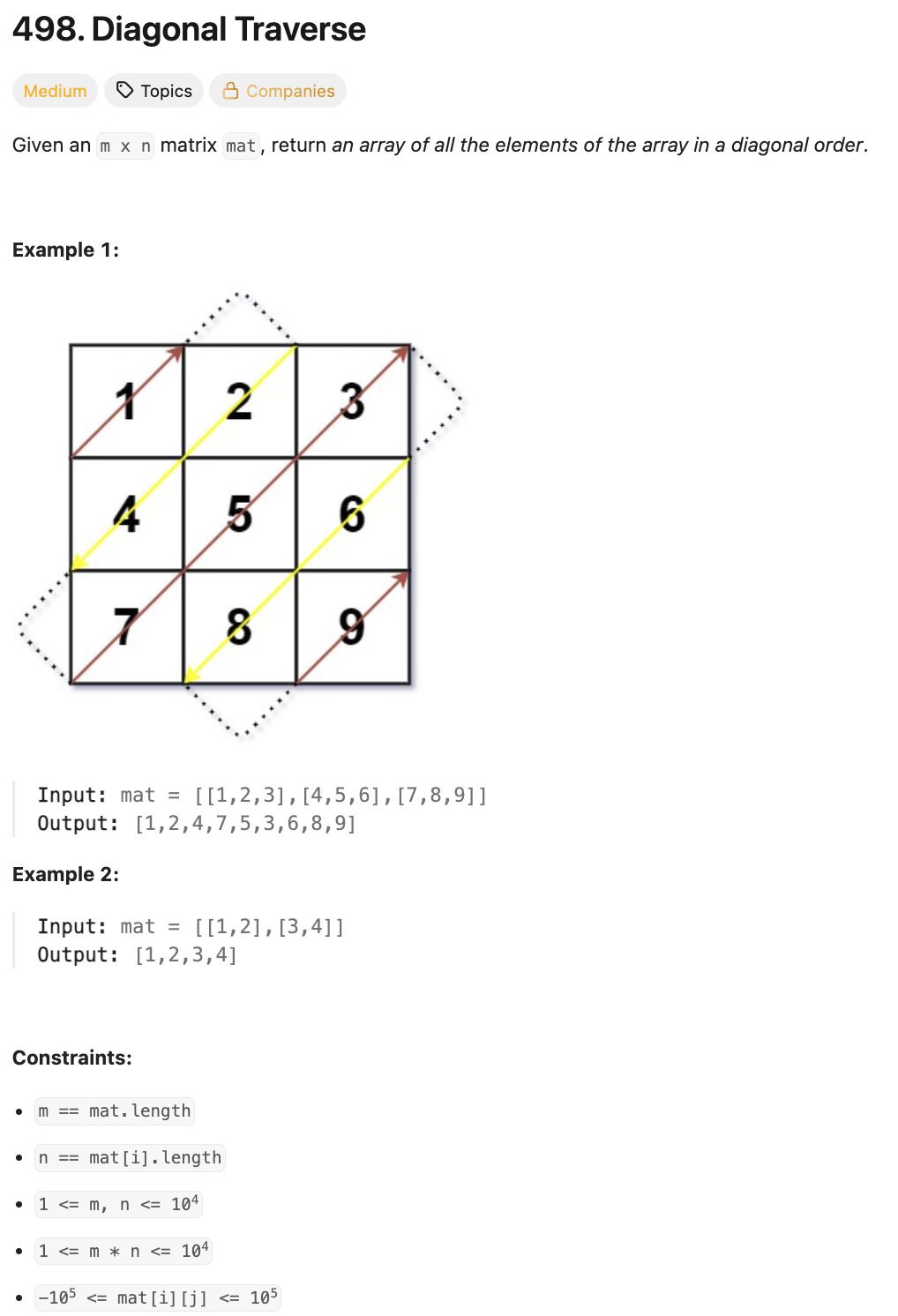
📌 문제 : Leet Code 498

---

📌 문제 탐색하기

mat : 입력되는 행렬
m, n : 행렬의 세로, 가로 크기 ($1 ≤ m, n ≤ 10^4, 1 ≤ m*n ≤ 10^4$)
mat[i][j] : 행렬 내 숫자 ($-10^5 ≤ mat[i][j] ≤ 10^5$)

문제 풀이

m x n 크기의 matrix가 주어졌을 때 대각선에 있는 순서대로 요소들을 담은 리스트를 반환하는 문제이다.

📖 행렬의 대각선 위치에 있는 원소들의 규칙

• 각 원소의 행 인덱스 i와 열 인덱스 j의 합 i + j가 같으면 같은 대각선에 속한다‼️
• 가로 세로 크기가 같지 않은 행렬에서도 동일하게 동작
• 대각선 수 = m + n - 1

위와 같은 대각선 위 원소들의 규칙을 적용해서 이중 for문으로 matrix 내 동일 대각선에 위치한 원소들을 찾는다.

단, 대각선이 짝수번째인지 홀수번째인지에 따라 배열 순서를 변경해주어야 한다.

• 짝수 : 위에서 아래로 이동 → 리스트 역순 정렬 필요
• 홀수 : 아래에서 위로 이동

가능한 시간복잡도

2중 for문으로 matrix 탐색 → $O(m*n) = O(mn)$
리스트 역순 → $O(m*n) = O(mn)$

최종 시간복잡도
최악의 경우 $O(mn) = O(10^4)$이므로 충분히 동작할 수 있다.

알고리즘 선택

• 2중 for문으로 matrix에 접근해 대각선 위치에 있는 원소들 탐색

---

📌 코드 설계하기

1. 동일 대각선 상 요소 저장할 리스트 정의
2. 대각선 접근
3. 정답 저장 리스트 저으이
4. 대각선 저장 리스트를 접근하며 대각선 순서에 따라 배열 순서 변경
5. 결과 반환

---

📌 시도 회차 수정 사항

1회차

• 문제 이해를 잘못해서 왼쪽 아래에서 오른쪽 위로 이동하는 방향으로 구현하려 했다. 4중 for문을 쓰면서 구현했지만 결과도 이상하고 숫자를 읽는 순서도 잘못 되었다.

---

📌 정답 코드

class Solution:
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        # 크기 정의
        m, n = len(mat), len(mat[0])

        # 대각선 개수 만큼 리스트 정의
        diagonals = [[] for _ in range(m + n - 1)]

        # 대각선 접근
        for i in range(m):
            for j in range(n):
                diagonals[i+j].append(mat[i][j])
        
        # 정답 저장 리스트 정의
        answer = []

        # 대각선 순서에 따라 배열 순서 변경
        for z in range(m + n - 1):
            # 짝수번째면 역순
            if z % 2 == 0:
                answer.extend(diagonals[z][::-1])
            # 홀수번째면 바로 추가
            else:
                answer.extend(diagonals[z])
        
        return answer

• 결과
  

---

👍 다른 풀이

class Solution:
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
    	# 행과 열의 개수 저장
        amnt_rows, amnt_cols = len(mat), len(mat) 
        
        # 시작 위치: 맨 왼쪽 위 (0,0)
        r = c = 0
        
        # 결과를 저장할 리스트
        res = []  
        
        while True:
            # 모든 원소를 다 탐색하면 종료
            if len(res) >= amnt_rows * amnt_cols:
                break
            
            # 현재 위치의 값 저장
            res.append(mat[r][c])  
            
            # 현재 대각선의 방향 결정: (r+c)%2==0이면 위↗ 방향, 아니면 아래↙ 방향
            if (r + c) % 2 == 0:  # 위로 올라가며 오른쪽으로(↗)
                if c == amnt_cols - 1:  # 맨 오른쪽 열에 도달한 경우
                    r += 1  # 아래 행으로 내려감
                elif r == 0:  # 맨 위 행에 도달한 경우
                    c += 1  # 오른쪽으로 한 칸 이동
                else:
                    r -= 1  # 행을 위로 한 칸 이동
                    c += 1  # 열을 오른쪽으로 한 칸 이동
            else:  # 아래로 내려가며 왼쪽으로(↙)
                if r == amnt_rows - 1:  # 맨 아래 행에 도달한 경우
                    c += 1  # 오른쪽으로 한 칸 이동
                elif c == 0:  # 맨 왼쪽 열에 도달한 경우
                    r += 1  # 아래 행으로 한 칸 이동
                else:
                    c -= 1  # 열을 왼쪽으로 한 칸 이동
                    r += 1  # 행을 아래로 한 칸 이동
        
        return res  # 대각선 순서대로 완성된 결과 리스트 반환

        

• Runtime : 3ms
• 경우별로 경계조건을 세세히 나누어 구현하는 방식이다. 리스트를 여러 개 정의하지 않고 역순으로 정렬하는 과정도 빠졌으며, 한 번 전체 matrix를 순회하면서 결과를 완성하므로 더 빠른 시간 안에 동작할 수 있는 것 같다.

---

✏️ 회고

• 동일 대각선 상 요소들의 특징은 꼭 기억했어야 했는데 잊었다. 잊더라도 규칙을 찾을 수 있어야 했는데 그러지도 못했다. 규칙 찾는게 너무 어렵다.