[파이썬/Python] Leet Code 933(Easy): Number of Recent Calls

숨·2025년 9월 2일

코테

알고리즘 문제 풀이

목록 보기

126/128

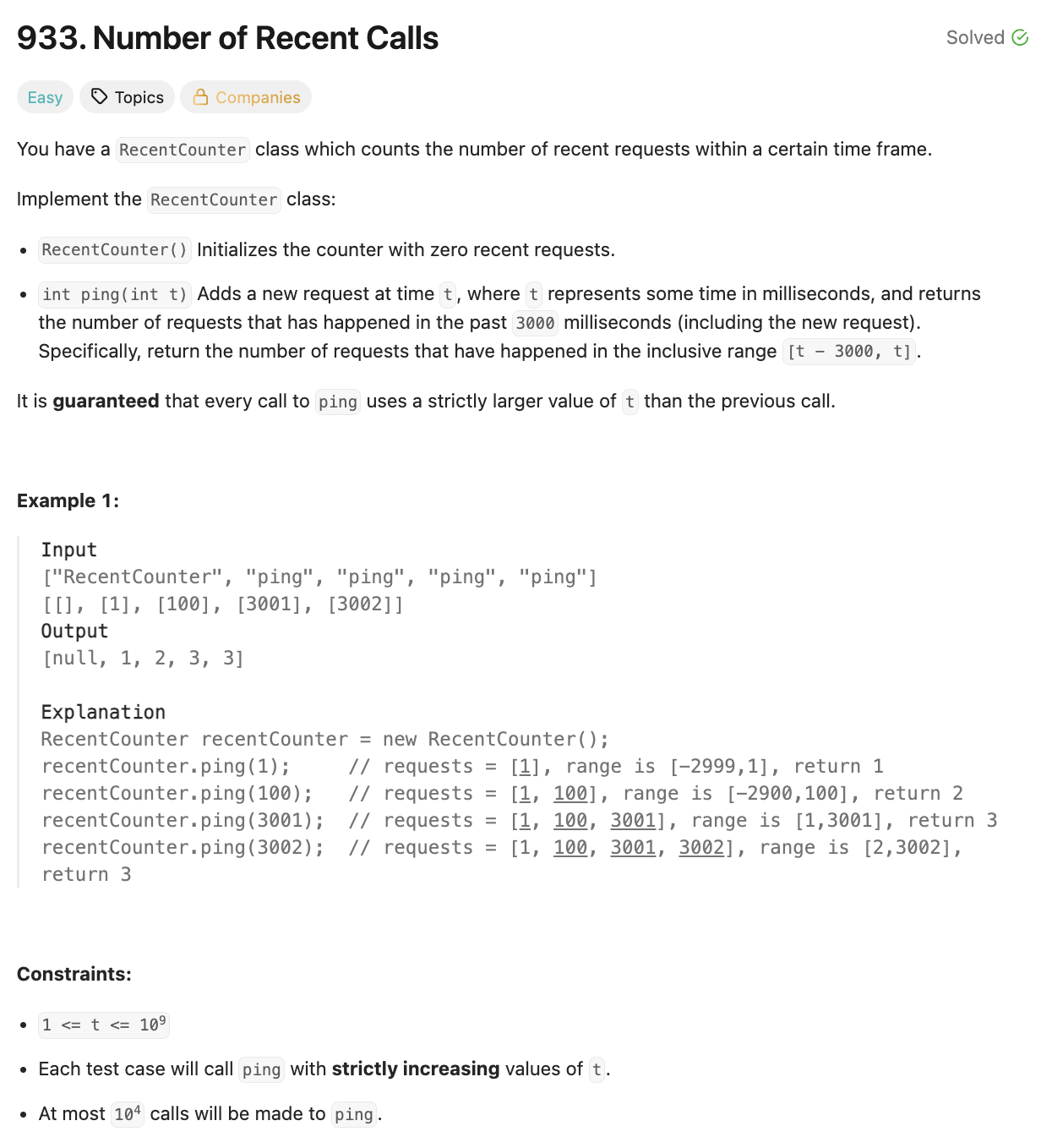
📌 문제 : Leet Code 933

📌 문제 탐색하기

t : 요청 시간 ( $1 ≤ t ≤ 10^9$ )

문제 풀이

특정 시간 내 최신 요청의 수를 세는 RecentCounter 클래스가 있다.

RecentCounter 클래스는

0개의 최신 요청으로 초기화
ping 함수 존재
- ms 단위의 시간을 의미하는 시간 t에서의 요청을 추가
- 새 요청을 포함해서 지난 3000ms초 내의 요청의 수를 반환
  - [t - 3000, t] 범위의 요청의 수 반환

이때, ping의 모든 call은 이전 call보다 더 큰 시간 t라는 것을 보장한다.
→ call은 시간 순서대로 들어온다!

이 문제는 RecentCounter 클래스를 조건에 따라 구현하는 문제이다.

__init__() 함수엔 요청 시간을 저장할 공간을 정의하도록 구현하고,
ping() 함수엔 입력된 요청을 추가하고 최신 요청 시간으로부터 3000ms 사이의 요청만 저장하여 그 요청을 저장한 리스트의 길이를 반환하도록 구현하면 된다.

가능한 시간복잡도

while → $O(3000)=O(1)$

최종 시간복잡도
최악의 경우에도 $O(1)$ 로 상수 시간이므로 충분히 동작할 수 있다.

알고리즘 선택

while문으로 3000ms 밖의 요청은 삭제하기

📌 코드 설계하기

init 함수 구현
1-1. 요청 시간 저장할 큐 정의
ping 함수 구현
2-1. 요청 시간 저장
2-2. 3000ms외의 요청 제거
2-3. 요청 개수 반환

📌 시도 회차 수정 사항

📌 정답 코드

from collections import deque

class RecentCounter:

    def __init__(self):
        # 요청 시간 저장할 큐 정의
        self.pings = deque()
        

    def ping(self, t: int) -> int:
        # 요청 시간 저장
        self.pings.append(t)

        # 3000ms외의 요청 제거
        while self.pings and self.pings[0] < t - 3000:
            self.pings.popleft()
        
        # 요청 개수 반환
        return len(self.pings)


# Your RecentCounter object will be instantiated and called as such:
# obj = RecentCounter()
# param_1 = obj.ping(t)

결과

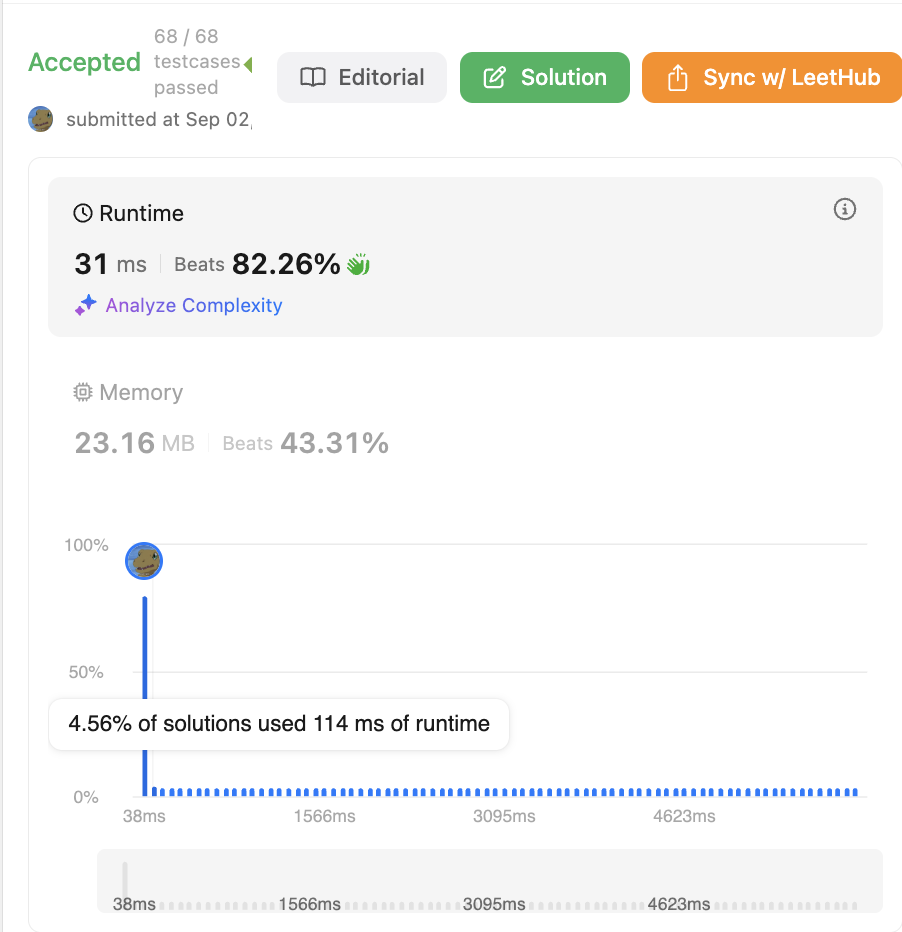
👍 다른 풀이

from bisect import bisect_left

class RecentCounter:

    def __init__(self):
    	# 요청 시간 저장 리스트(오름차순)
        self.pings = [] 
        

    def ping(self, t: int) -> int:
    	# 새 요청 추가
        self.pings.append(t)
        
        # 최근 3000m초의 시작 시간 계산
        tStart = t - 3000 
        
        # 3000ms초 내에 있는 첫번째 요청 인덱스 찾기
        tStartPos = bisect_left(self.pings, tStart)
        
        # 3000ms초 내의 요청 개수 반환
        return len(self.pings)-tStartPos

        
# Your RecentCounter object will be instantiated and called as such:
# obj = RecentCounter()
# param_1 = obj.ping(t)