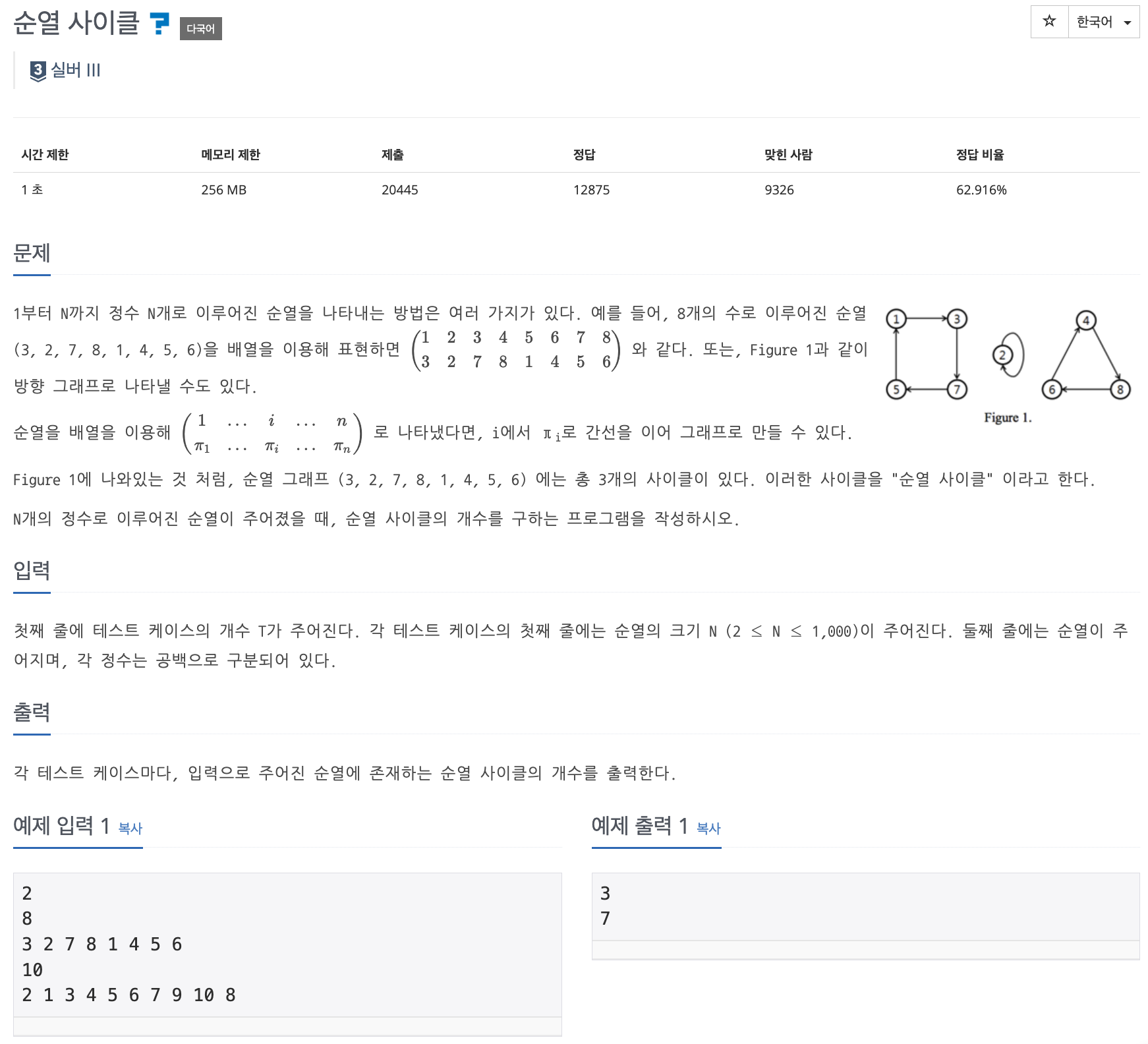
📌 문제 : 백준 10451번
📌 문제 탐색하기
T : 테스트케이스 수
N : 순열의 크기 (2 ≤ N ≤ 1,000)
✅ 입력 조건
1.T입력
2.N입력
3.N개의 숫자로 이루어진 순열 공백 구분해 입력
✅ 출력 조건
1. 테스트 케이스 별 출력
2. 순열에 존재하는 순열 사이클 개수 출력
주어진 N개의 정수 순열에서 순열 사이클 개수를 구하는 문제이다.
입력 받은 N개의 정수는 1부터 N까지 차례대로 어떤 숫자와 연결되어 있는지를 의미한다.
(3, 2, 7, 8, 1, 4, 5, 6)이 입력으로 들어온다면,
1→3, 2→2, 3→7, 4→8, 5→1, 6→4, 7→5, 6→8
이런 식의 가중치 없는 연결 정보를 얻게 되는 것이다.
가중치가 없으므로 가중치 없는 인접 리스트로 그래프를 표현한다.
연결에 방향성이 있으므로 단방향 그래프에 입력 정보를 저장해야 한다.
graph[start] = end
이와 같이 연결 정보를 저장하므로
start부분에 1부터 N까지의 정수를 차례대로 넣고,
end에 해당 순서의 입력 받은 정수를 넣으면 될 것이다.
연결 정보를 모두 저장한 후, 탐색을 통해 사이클 수를 계산한다.
BFS를 구현하기 위해 collections의 deque를 호출한다.
큐로 BFS를 정의하고 수행해서 연결된 모든 노드를 탐색한다.
그래프를 돌면서 방문 안된 연결 노드가 있으면 BFS를 계속 수행하는 식으로 구현한다.
한번 BFS가 끝나면 연결된 사이클을 하나 찾았다고 할 수 있으므로,
그 횟수를 세어 전체 순열 사이클 개수를 계산한다.
가능한 시간복잡도
그래프 저장 →
BFS 수행 →
최종 시간복잡도
테스트케이스 수 제외하면 으로,
최악의 경우, N이 최대 1000일 때
이 되어 1초 내로 계산이 가능할 것 같다.
알고리즘 선택
그래프에 숫자 간 연결 정보를 저장하고 BFS로 사이클 횟수 계산하기
📌 코드 설계하기
- BFS 정의
1-1. 방문 처리
1-2. 큐가 빌 때까지 반복
1-3. 해당 노드 연결 정보 확인
1-4. 방문 안했다면 방문 처리 - 정답 저장 리스트 정의
- T 입력
- N 입력
- 그래프 정의
- N개 숫자 순열 입력
- 그래프에 저장
- 방문 리스트 정의
- 횟수 변수 정의
- 그래프 돌면서 BFS 수행
10-1. 횟수 세기 - 횟수 정답 리스트에 저장
- 원하는 형식으로 출력
📌 시도 회차 수정 사항
1회차
📌 정답 코드
import sys
from collections import deque
input = sys.stdin.readline
# 1. BFS 정의
def bfs(x):
queue = deque([x])
# 방문 처리
visited[x] = 1
# 큐가 빌 때까지 반복
while queue:
v = queue.popleft()
# 해당 노드 연결 정보 확인
for i in graph[v]:
# 방문 안했다면
if not visited[i]:
visited[i] = 1
queue.append(i)
# 2. 정답 저장 리스트
answer = []
# 3. T 입력
T = int(input())
for _ in range(T):
# 4. N 입력
N = int(input())
# 5. 그래프 정의
graph = [[] for _ in range(N + 1)]
# 6. N개 숫자 순열 입력
nums = list(map(int, input().split()))
# 7. 그래프에 저장
for i in range(1, N + 1):
graph[i].append(nums[i - 1])
# 8. 방문 리스트 정의
visited = [0] * (N + 1)
# 9. 횟수 변수 정의
count = 0
# 10. 그래프 돌면서 BFS 수행
for i in range(1, N + 1):
if not visited[i]:
# bfs 수행
bfs(i)
# 횟수 세기
count += 1
# 11. 정답 저장
answer.append(count)
# 12. 원하는 형식으로 출력
for count in answer:
print(count)- 결과

📌 회고
- 그래프 문제는 DFS/BFS와 무엇이 다른지 궁금했는데, 그 두 방법이 그래프 문제를 푸는 방법 중 일부였다는 것을 알게 되었다. 그 외에도 사용할 수 있는 알고리즘이 다양하다는 것을 알 수 있었다.
📌 기억할 정보
📖 그래프 표현 방법 3가지
-
에지 리스트 (edge list)
- 에지 중심으로 그래프 표현
- 👍 구현 쉬움
- 벨만-포드(노드 간 최단 거리 찾기), 크루스칼(최소 신장 트리 찾기) 알고리즘에 사용 ⭕️
- 👎 특정 노드 관련 에지 탐색 어려움
- 노드 중심 알고리즘엔 잘 사용 ❌
- 가중치 없는 그래프
- 출발 노드, 도착 노드 표현 → 리스트 열 2개
- 가중치 있는 그래프
- 출발 노드, 도착 노드, 가중치 표현 → 리스트 열 3개
-
인접 행렬 (adjacency metrix)
- 노드 중심으로 그래프 표현 → 2차원 리스트 이용
- 👍 두 노드 연결 에지 여부, 가중치 값 바로 확인 가능
- 👎 노드 관련 에지 탐색 시 N번 접근
- 시간 복잡도 느림
- 노드 개수에 비해 에지 적으면 공간 효율성 🔻
-
인접 리스트 (adjacency list)
- 노드 개수만큼 리스트 선언
- 👍 노드 연결 에지 탐색 시간 뛰어남, 노드 개수 커도 공간 효율 좋아 메모리 초과 에러 발생 ❌
- 👎 구현 복잡