[파이썬/Python] 백준 11060번: 점프 점프

숨·2024년 9월 28일

코테

알고리즘 문제 풀이

목록 보기

88/105

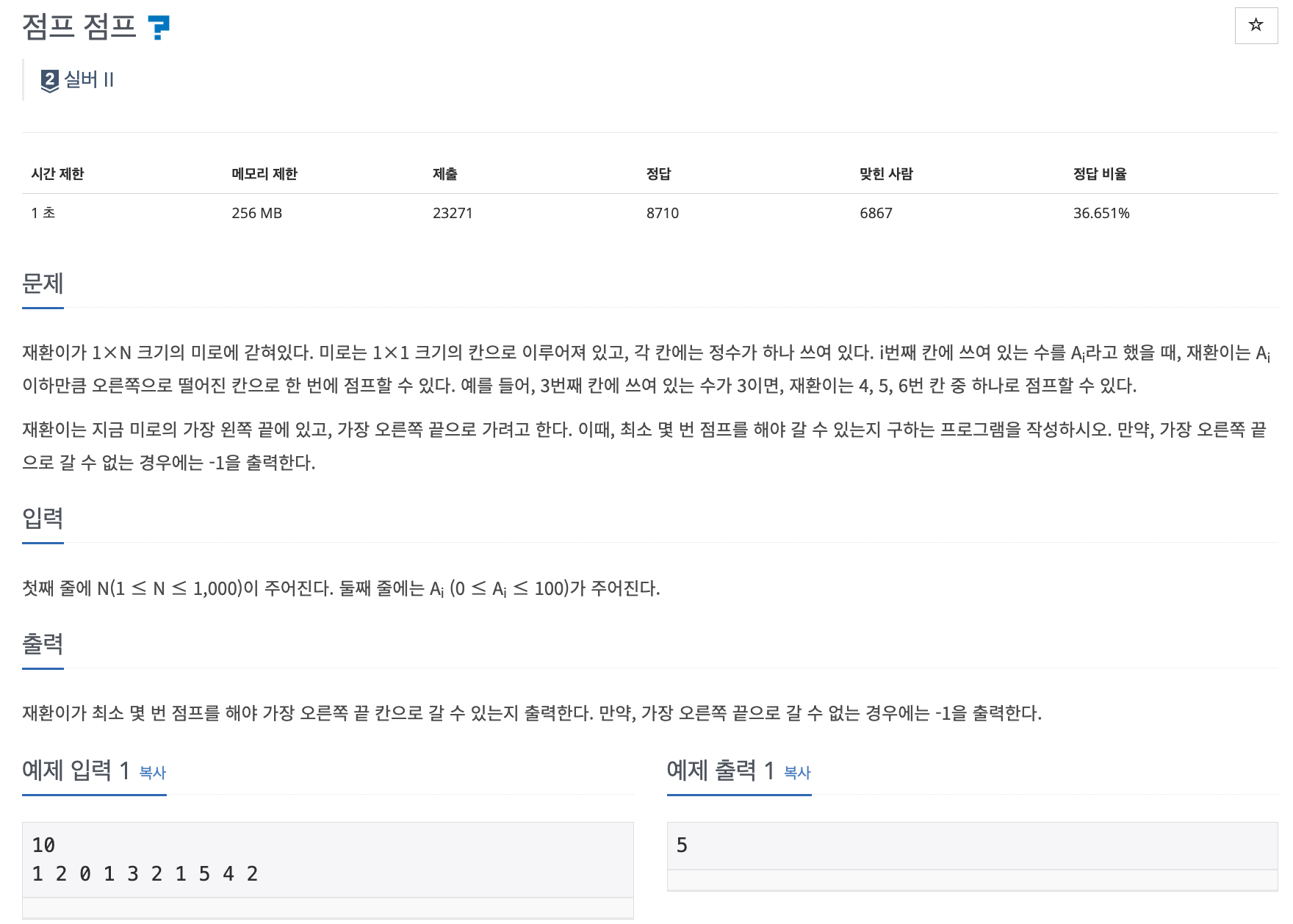
📌 문제 : 백준 11060번

📌 문제 탐색하기

N : 미로의 가로 크기 $(1 ≤ N ≤ 1,000)$
Ai : i번째 칸에 쓰여 있는 수 $(0 ≤ Ai ≤ 100)$

맨 왼쪽에서 맨 오른쪽으로 가기 위해 점프하는 최소 횟수를 구하는 문제이다.

문제 풀이

⭐️ 점프하는 방법

현재 칸이 i번째라면?

해당 칸에 위치한 값 Ai 확인

Ai 이하의 값만큼 이동 가능

예) i = 3이라면?

1칸, 2칸, 3칸 점프 가능

이동 불가능하다면 -1 출력

0번째 칸에서 N-1번째 칸까지 가는 최단 경로를 찾는 문제이다.
최소 점프하는 경우는 이전에 점프한 경우에서 모두 최소 점프 횟수를 가지게 된다.
→ DP를 이용해 이 문제를 해결한다.

💡 DP 구현하기

모든 칸에 대해 점프 횟수를 기록할 DP 테이블 정의

DP 테이블 초기화

도달 가능 파악을 위한 방문 여부 및 최소 횟수 갱신을 위해 최댓값으로 채우기

첫번째 이동 = 점프 횟수 0번

결과 구하기

기존 칸의 값과 현재 계산한 최소 점프 횟수 중 더 작은 수로 갱신

마지막 N-1번째에서 원하는 최소 점프 횟수 반환

해당 위치에 저장된 점프 횟수가 없다면 -1 반환

가능한 시간복잡도

이중 for문으로 dp 테이블 채우기 → $O(N * len(A))$

최종 시간복잡도
최악의 경우 $O(1000 * 100)$ 이 되어 1초 내에 연산 가능하다.

알고리즘 선택

이동 가능한 경우를 for문으로 접근해 모든 점프 횟수를 계산하는 DP 이용하기

📌 코드 설계하기

필요한 입력 받기
dp 테이블 정의
dp 테이블 초기화
dp 테이블 채우기
결과 출력

📌 시도 회차 수정 사항

1회차

처음에 DP 테이블을 -1로 초기화해서 마지막 인덱스 도달 여부를 if dp[N-1] == -1:라는 조건으로 판단했었는데 최솟값 갱신을 위한 min()함수를 사용하기 위해 최댓값으로 변경했었다.
조건을 변경하였다.

2회차

예시가 모두 동작하는데 계속 틀렸다는 결과를 얻었다.
$(0 ≤ Ai ≤ 100)$ 라는 조건을 생각해서 dp 테이블을 101로 채웠었다. 이 값은 점프 횟수에 대한 범위가 아니기 때문에 최댓값을 101로 잡는 것은 잘못된 것이다.
N칸보다 많이 점프할 수 없기 때문에 N의 최댓값에서 1 더한 1001로 변경하여 dp 테이블을 채웠다.

📌 정답 코드

import sys

input = sys.stdin.readline

# N 입력
N = int(input())

# A 입력
A_list = list(map(int, input().split()))

# dp 테이블 정의
dp = [1001] * N

# dp 테이블 초기화
dp[0] = 0

for i in range(N):
    # 점프할 수 있는 범위 탐색
    for j in range(1, A_list[i] + 1):
        # 범위 내인지 확인
        if i + j < N:
            # 최소 점프 횟수 갱신
            dp[i + j] = min(dp[i + j], dp[i] + 1)

# 도달 여부 확인
if dp[N-1] == 1001:
    print(-1)
else:
    print(dp[N-1])