[파이썬/Python] 백준 1149번: RGB거리

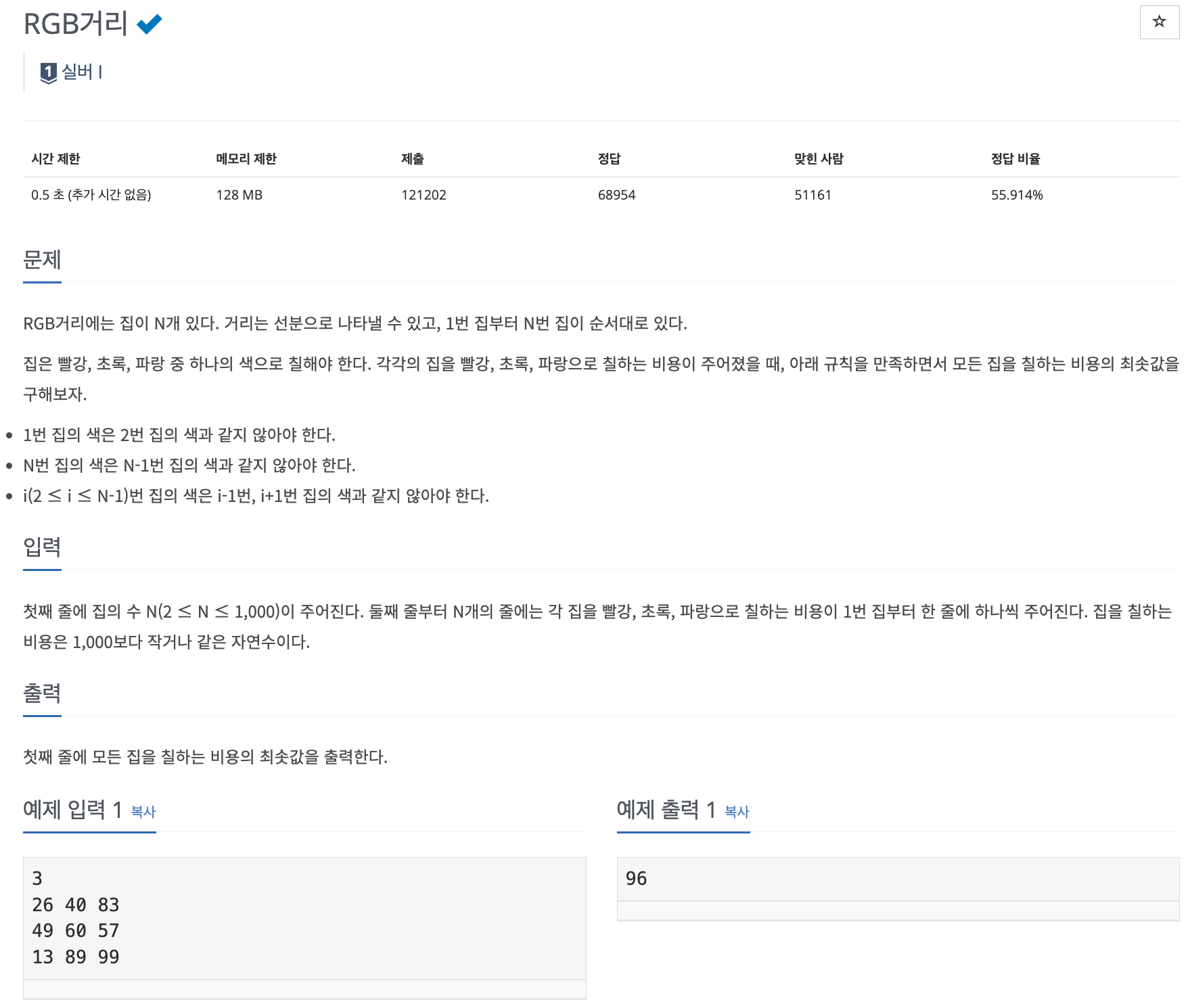
📌 문제 : 백준 1149번

---

📌 문제 탐색하기

N : 집의 개수 $(2 ≤ N ≤ 1,000)$

입력받은 각각의 집을 칠하는 비용을 활용해 규칙을 만족하면서 집 칠하는 비용의 최솟값을 구하는 문제이다.

문제 풀이

⭐️ 집 칠하는 규칙

• 1번 집 색 ≠ 2번 집 색
• N번 집 색 ≠ N-1번 집 색
• i번 집 색 ≠ i-1번 집 색, i+1번 집 색

위의 규칙에 따라 서로 접하는 위치의 집끼리 같은 색을 칠하면 안된다는 것을 알 수 있다.

이 조건을 지키면서 첫번째 집을 칠할 때부터, 매 순간 이전 집과 다른 색을 칠하는 경우 중 더 적은 비용이 드는 색을 선택하도록 구현한다.
→ 이전 단계가 이후 단계에 영향을 주기 때문에 DP를 활용하면 될 것이다.

첫번째 집의 색을 선택할 때 최소의 비용을 선택한다고 해서 전체 비용이 최소가 될 것이란 보장이 없다.
→ 3가지 색 각각으로 시작할 때의 비용에 대한 모든 경우를 구해야 할 것이다.

따라서 DP 테이블을 N * 3 크기로 정의해서 DP를 수행한다.

• 첫번째 집에 해당하는 인덱스 0
  • 첫번째 집의 비용 똑같이 넣기
• 인덱스 1부터 N번째 집에 해당하는 인덱스 N-1까지
  • 이전 집과 다른 색 중 더 적은 비용 합산하기

가능한 시간복잡도

N개의 집에 대한 색칠 비용으로 DP 테이블 채우기 → $O(N)$

최종 시간복잡도
$O(N)$으로 최악의 경우 $O(1000)$이 되는데 이는 0.5초내 연산이 가능하다.

알고리즘 선택

DP를 통해 최소 비용이 들도록 색칠하는 모든 경우 찾기

---

📌 코드 설계하기

1. 필요한 입력 받기
2. DP 테이블 정의
3. DP 테이블 초기화
4. DP 테이블 채우기
5. 결과 출력
   
   

---

📌 시도 회차 수정 사항

1회차

---

📌 정답 코드

import sys

input = sys.stdin.readline

# N 입력
N = int(input())

# 색칠 비용 입력
prices = [list(map(int, input().split())) for _ in range(N)]

# DP 테이블 초기화
dp = [[0] * 3 for _ in range(N)]
dp[0] = prices[0]

# DP 계산
for i in range(1, N):
    # 빨강으로 칠할 경우
    dp[i][0] = min(dp[i-1][1], dp[i-1][2]) + prices[i][0]
    # 초록으로 칠할 경우
    dp[i][1] = min(dp[i-1][0], dp[i-1][2]) + prices[i][1]
    # 파랑으로 칠할 경우
    dp[i][2] = min(dp[i-1][0], dp[i-1][1]) + prices[i][2]  

# 결과 출력
print(min(dp[N-1]))

• 결과