[파이썬/Python] 백준 13702번: 이상한 술집

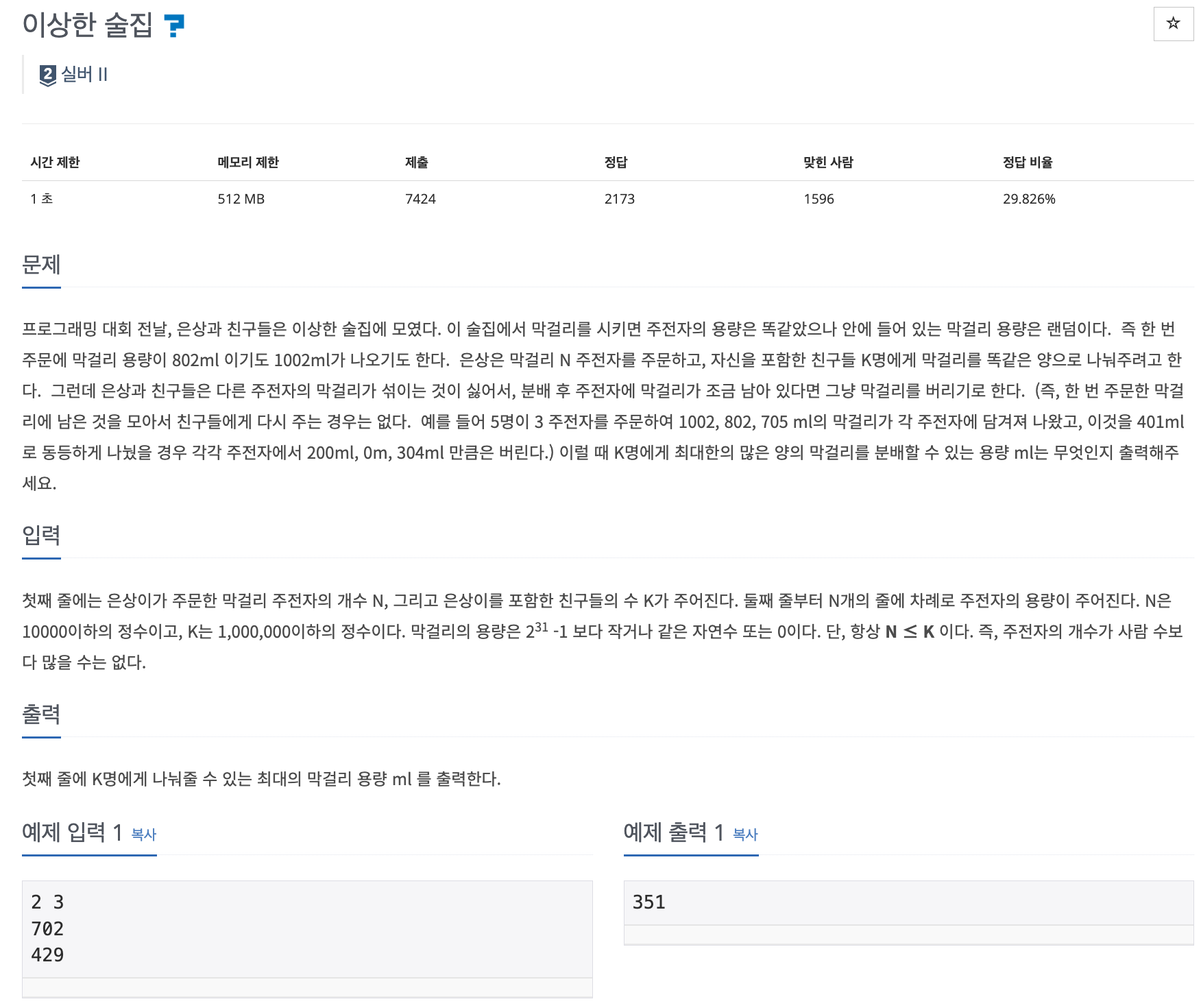
📌 문제 : 백준 13702번

---

📌 문제 탐색하기

N : 막걸리 주전자 개수 $(0 ≤ N ≤ 10000)$
K : 친구들의 수 $(0 ≤ K ≤ 1,000,000)$

주전자의 개수가 사람 수보다 많을 수는 없다.$(N ≤ K)$

분배할 수 있는 막걸리의 최댓값을 구하는 문제이다.

문제 풀이

⭐️ 막걸리 분배 방법

• K명에게 똑같은 양의 막걸리 분배
• 다른 주전자의 막걸리 섞이면 ❌
• K명에게 최대한 많은 양의 막걸리 분배해야 함

변수의 범위가 매우 크기 때문에 시간 복잡도를 줄일 수 있는 방법을 사용해야 할 것이다.
→ 이분 탐색을 활용한다!

이분 탐색을 통해 막걸리 양을 적절히 조절하면서 모든 사람에게 동일한 양을 나눠줄 수 있는 최댓값을 구한다.

이분 탐색 구현

• 분배할 수 있는 막걸리양은 막걸리 용량 중 최댓값을 넘을 수 없다.
  • 이분탐색 범위 → 1 ~ 용량 최댓값 사이로 지정한다.
• 범위의 중앙값 ﹦ 분배할 막걸리 양를 의미하므로 분배 조건에 맞는지 확인한다.
  • K명을 나눠줄 수 있는가?
    • 각 주전자 용량을 막걸리양으로 나누어 나눠줄 수 있는 사람 수 계산
    • 사람 수가 K보다 크거나 같으면 나눠줄 수 있음
• 가능 여부에 따라 탐색을 진행한다.
  • 가능하다 → 탐색 범위를 늘려 용량을 키워본다
  • 불가능하다 → 탐색 범위를 줄여 용량을 줄인다

가능한 시간복잡도

주전자 입력 → $O(N)$
이분탐색 내에서 사람 수 계산 → $O(N * log(max(pots)))$

최종 시간복잡도
$O(N * log(max(pots)))$이 되어 최악의 경우 $O(10000 * log(2^{31}-1 )) = O(310,000)$으로 1초 내 연산 가능하다.

알고리즘 선택

이분탐색으로 적절한 막걸리 용량 찾기

---

📌 코드 설계하기

1. 필요한 입력 받기
2. 이분탐색 범위 지정
3. 결과 저장 변수 정의
4. 이분탐색 진행
5. 결과 출력

---

📌 시도 회차 수정 사항

1회차

• 값을 입력하고 엔터 치기 전에 답이 반환되었는데 틀린 값이 나왔다.
• 확인해보니 각 주전자의 용량을 한줄씩 입력받는데 아래와 같이 한줄에 모두 입력받아 처리하는 식으로 입력받아서 잘못된 결과를 얻는 것이었다.

# 주전자 용량 입력
pots = list(map(int, input().split()))

2회차

• 런타임 에러 (ZeroDivisionError)가 발생했다. 이는 0을 나눌 때 발생하게 된다.
• 이분탐색 범위를 0부터 진행했는데 이부분에서 mid가 0이 되는 경우가 생겨 발생한 것 같다. 이분탐색 지점을 1부터 시작하도록 변경했다.

---

📌 정답 코드

import sys

input = sys.stdin.readline

# N, K 입력
N, K = map(int, input().split())

# 주전자 용량 입력
pots = [int(input()) for _ in range(N)]

# 이분탐색 범위 지정
start = 1
end = max(pots)

# 결과 저장 변수
answer = 0

# 이분탐색 진행
while start <= end:
    # 중앙값 지정
    mid = (start + end) // 2

    # 나눠줄 수 있는 사람 수 계산
    count = 0
    for pot in pots:
        count += pot // mid

    # 나눠줄 수 있는지 여부 확인
    if count >= K:
        # 가능하니까 저장 후 범위 늘리기
        answer = mid
        start = mid + 1
    else:
        # 불가능하니까 범위 좁히기
        end = mid - 1

# 결과 출력
print(answer)

• 결과