[파이썬/Python] 백준 1577번: 도로의 개수

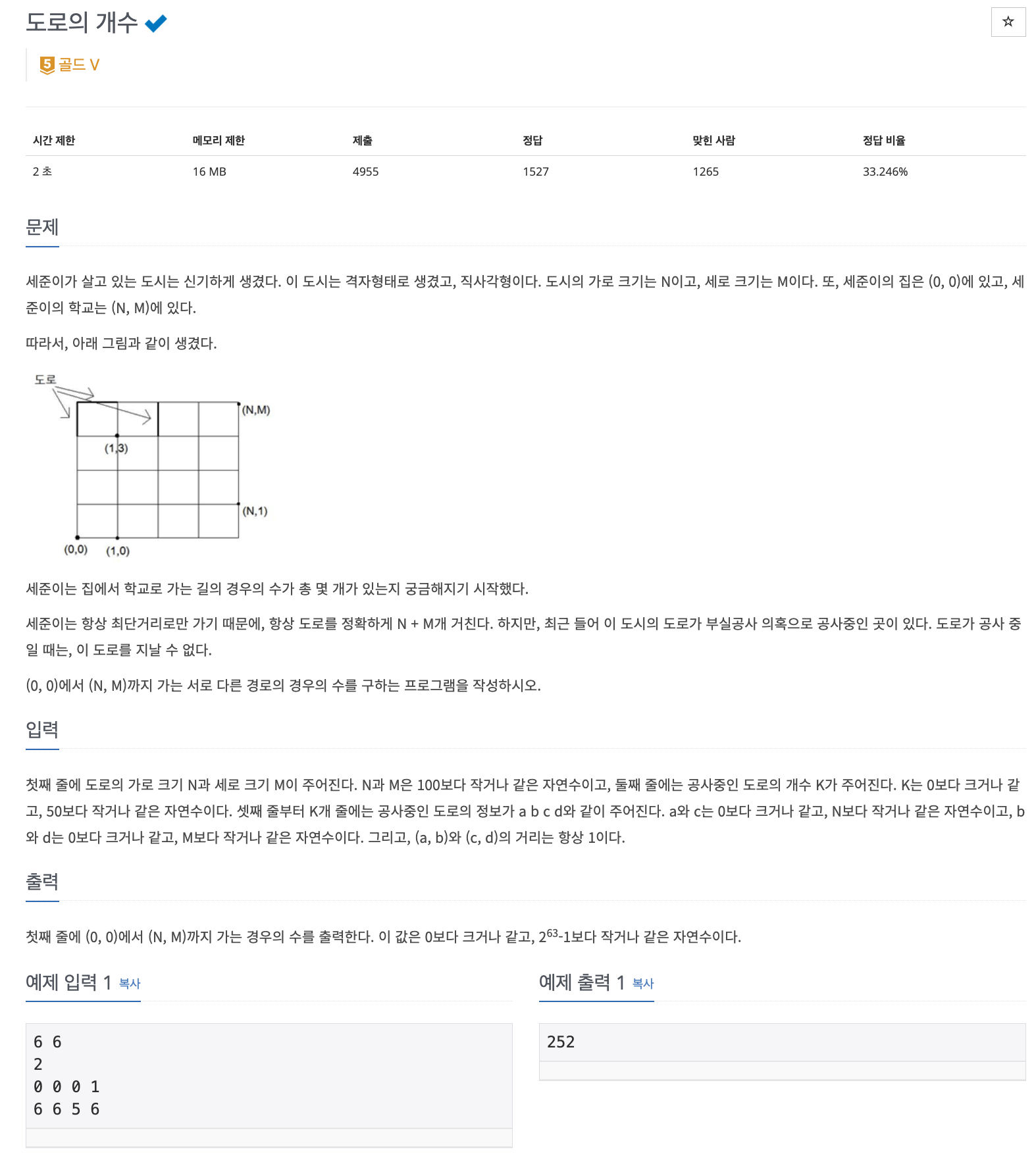
📌 문제 : 백준 1577번

---

📌 문제 탐색하기

N : 도시의 가로 크기 $(1 ≤ N ≤ 100)$
M : 도시의 세로 크기 $(1 ≤ M ≤ 100)$
K : 공사중인 도로 개수 $(0 ≤ K ≤ 50)$
a, b, c, d : 공사중인 도로 정보 $(0 ≤ a, c ≤ N, 0 ≤ b, d ≤ M)$

지날 수 없는 도로를 제외하고 (0, 0)에서 (N, M)까지 가는 서로 다른 경로의 경우의 수를 구하는 문제이다.

문제 풀이

⭐️ 가는 방법

• 항상 최단 거리 → 항상 왼쪽 위에서 오른쪽 아래로 이동한다.
• (a, b), (c, d) 형식으로 입력받은 곳은 지나가지 못한다.

이동은 항상 동일하게 최단 거리로 가는 방향으로 진행하기 때문에,
(0, 0)에서 특정 위치까지의 최단 거리는 그 위치의 위의 점, 왼쪽의 점까지 오는 각각의 최단 거리의 합과 동일하다.

즉, 어느 한 점의 최단거리의 개수는 그 점으로 갈 수 있는 점들의 최단거리의 개수의 합과 동일하다❗️

이 사실을 점화식으로 표현하면 DP로 문제를 해결할 수 있다.
DP에 저장될 값이 해당 위치까지의 최단 거리라고 한다면, dp[N][M]에 원하는 값을 저장하게 된다.

점화식은 다음과 같이 표현된다.
dp[i][j] = dp[i-1][j] + dp[i][j-1]

초기값 dp[0][0] = 1이라 할 수 잇다.
공사 도로의 dp값에 0을 미리 채워준다면, 공사 도로를 고려하면서 계산할 수 있을 것이다.

⭐️ DP 구현하기

• 점화식 : dp[i][j] = dp[i-1][j] + dp[i][j-1]
• 초기값 : dp[0][0] = 1
• 공사 도로 : dp[a][b] = 0, dp[c][d] = 0

전체 지도 정보를 저장할 N * M의 공간을 만들어 준 후,
공사 도로에 대한 정보를 따로 저장한다.
이중 for문으로 위의 내용과 같이 값을 채워주고,
dp[N][M]을 출력한다.

가능한 시간복잡도

이중 for문으로 dp 테이블 채우기 → $O(N * M)$

최종 시간복잡도
$O(N * M)$로 최악의 경우 $O(10000)$이 되어 2초 내에 연산할 수 있다.

알고리즘 선택

DP로 최단 거리 계산

---

📌 코드 설계하기

1. N, M 입력
2. K 입력
3. 공사 도로 입력
4. 지도 정보 초기화
5. dp값 채우기
6. 결과 출력

---

📌 시도 회차 수정 사항

1회차

• 공사 도로의 위치를 단순히 (a, b), (c, d) 좌표로 접근했더니, dp값이 제대로 계산되지 않았다.
• 공사 도로는 (a, b), (c, d) 사이의 도로를 의미한 것인데 공그 지점 자체를 도로라고 생각하고 잘못 구현했다.
• 두 지점의 연결 정보 자체를 저장해서 dp값 계산 시, 연결 지점을 지나는 지를 확인하는 식으로 변경했더니 해결했다.

2회차

• 지도를 위한 2차원 배열을 저장할 때, N과 M 위치를 반대로 작성해 IndexError가 났다.

---

📌 정답 코드

import sys

input = sys.stdin.readline

# N, M 입력
N, M = map(int, input().split())

# K 입력
K = int(input())

# 공사 도로 저장
no_enter = set()
for _ in range(K):
    a, b, c, d = map(int, input().split())
    no_enter.add((a, b, c, d))
    no_enter.add((c, d, a, b))

# 지도 정보 입력
map_info = [[0] * (M + 1) for _ in range(N + 1)]
map_info[0][0] = 1

for m in range(M + 1):
    for n in range(N + 1):
        # 범위 내에 있는 직전 점 찾아 dp값 계산
        if n > 0 and (n - 1, m, n, m) not in no_enter:
            map_info[n][m] += map_info[n - 1][m]

        if m > 0 and (n, m - 1, n, m) not in no_enter:
            map_info[n][m] += map_info[n][m - 1]

print(map_info[N][M])

• 결과