[파이썬/Python] 백준 17086번: 아기 상어 2

숨·2024년 8월 10일

코테

알고리즘 문제 풀이

목록 보기

46/105

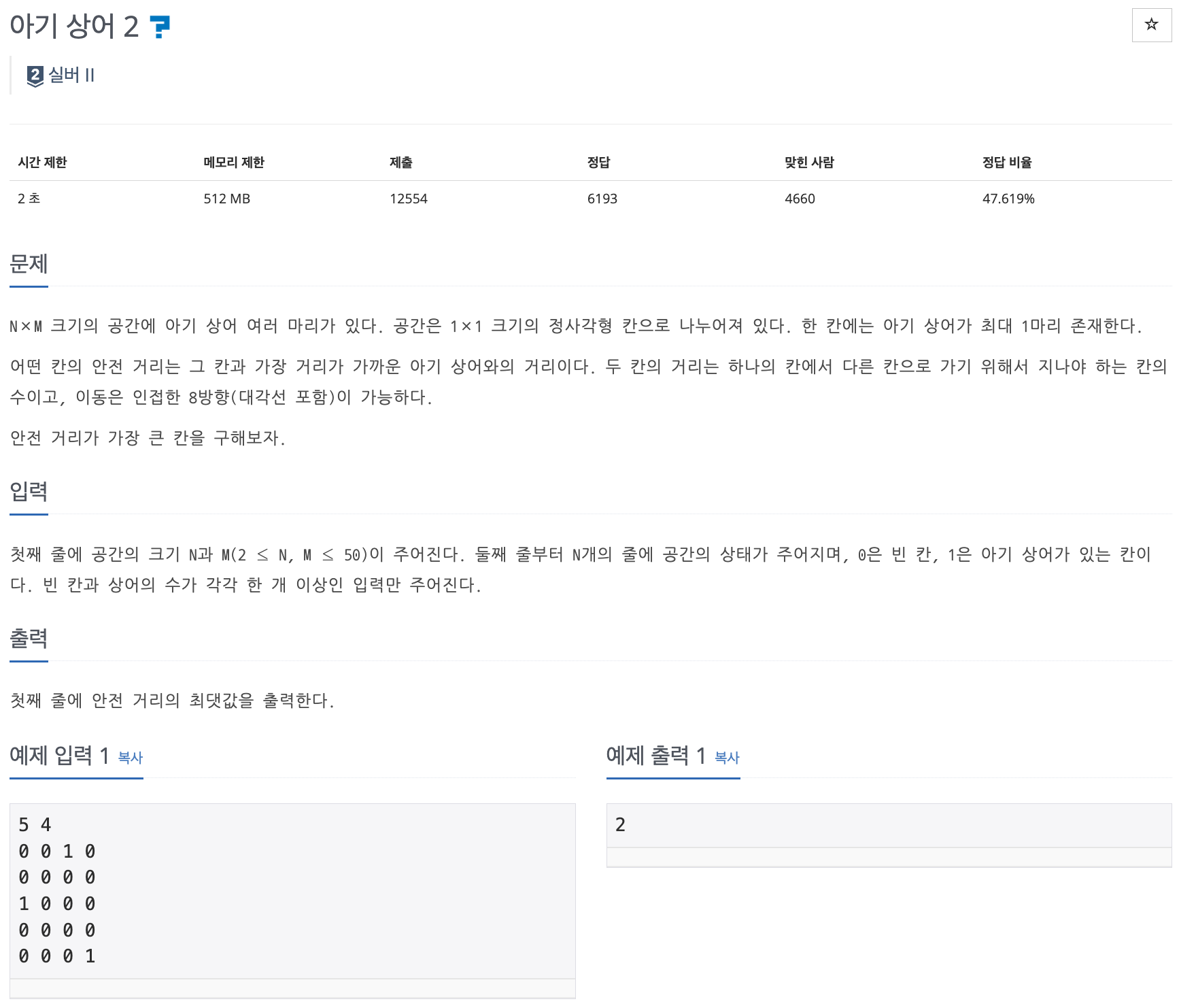
📌 문제 : 백준 17086번

📌 문제 탐색하기

N : 공간의 세로 크기 ( $2 ≤ N ≤ 50$ )
M : 공간의 가로 크기 ( $2 ≤ M ≤ 50$ )

✅ 입력 조건
1. N, M 입력
2. N번 반복해 공간 상태 입력
3. 0 → 빈칸 / 1 → 아기 상어 의미
✅ 출력 조건
1. 안전 거리의 최댓값 출력

안전 거리 : 해당 칸과 가장 거리가 가까운 아기 상어와의 거리를 의미
거리 : 한 칸에서 다른 칸으로 가기 위해 지나야 하는 칸의 수를 의미
이동 방향 : 8가지 (상, 하, 좌, 우, 대각선 4방향)

전체 공간을 돌면서 값이 아기 상어가 있는 위치를 의미하는 1의 위치를 찾고, 그 위치에서 BFS를 수행해 방문하지 않고 0을 가지는 칸을 탐색한다.

그 위치까지 몇 칸을 지났는지에 대한 변수를 정의하고, while문을 통해 8가지 방향을 확인하면서 그리드 내의 방문하지 않은 칸이 있다면 BFS를 수행하도록 구현한다.

이 과정을 진행하면서 칸 수를 1씩 증가하며 카운트해준다.

안전 거리가 가장 큰 칸을 구해야 하므로 위와 같이 카운트된 이동 칸수를 max() 함수를 통해 갱신해준다.

가능한 시간복잡도

공간 상태 입력 → $O(N * M)$
전체 공간에서 BFS → $O(N * M)$

최종 시간복잡도
$O(N * M)$
최악의 경우 $O(50^2) = O(2500)$ 이 된다.
이는 2초 내에 연산이 가능하다.

알고리즘 선택

전체 공간에서 상어 위치부터 시작하는 BFS 수행

📌 코드 설계하기

BFS 함수 구현
N, M 입력
N번 반복해 상태 입력
상어 위치 찾아 BFS 수행
결과 출력

📌 시도 회차 수정 사항

1회차

전체 공간을 돌면서 0을 가지는 칸에서 1을 발견할 때까지 BFS를 반복하는 식으로 이동 거리를 계산하려고 했다. 하지만 1이 여러 번 나올 수 있어서 어떻게 하면서 이미 방문한 1 외의 다른 1이 나오는 경우를 어떻게 해야 할지에 대한 아이디어가 떠오르지 않았다.
상어의 위치에서 시작해서 0인 칸 전체를 탐색하는 방향으로 변경했더니 방문 안한 칸마다 이동 횟수를 카운트하기만 해도 되었다. 따라서 이 방법으로 구현 방향을 변경했다.

📌 정답 코드

import sys
from collections import deque

input = sys.stdin.readline


# BFS 구현
def bfs(shark):
    # 이동 칸수 변수
    max_distance = 0
    queue = deque(shark)
    while queue:
        x, y, distance = queue.popleft()

        for direction in directions:
            nx, ny = x + direction[0], y + direction[1]
            # 공간 내 방문 안한 칸이라면 탐색 지속
            if 0 <= nx < N and 0 <= ny < M and graph[nx][ny] == 0:
                # 방문 처리 = 해당 칸까지의 이동 칸 수 저장
                graph[nx][ny] = distance + 1
                # 큐 저장
                queue.append((nx, ny, distance + 1))
                # 최대 거리 갱신
                max_distance = max(max_distance, distance + 1)
    return max_distance


# 8가지 방향 정의
directions = [(1, 0), (-1, 0), (0, 1), (0, -1), (1, 1), (1, -1), (-1, 1), (-1, -1)]

# N, M 입력
N, M = map(int, input().split())

# 그래프 초기화
graph = []

# 공간 상태 입력
for _ in range(N):
    graph.append(list(map(int, input().split())))

# 상어 위치 찾기
shark = []

for i in range(N):
    for j in range(M):
        if graph[i][j] == 1:
            # 상어 위치부터 시작할 것이므로 거리 0 추가
            shark.append((i, j, 0))

# 결과 출력
print(bfs(shark))