[파이썬/Python] 백준 1753(🥇4): 최단경로

숨·2025년 8월 14일

코테

알고리즘 문제 풀이

목록 보기

112/128

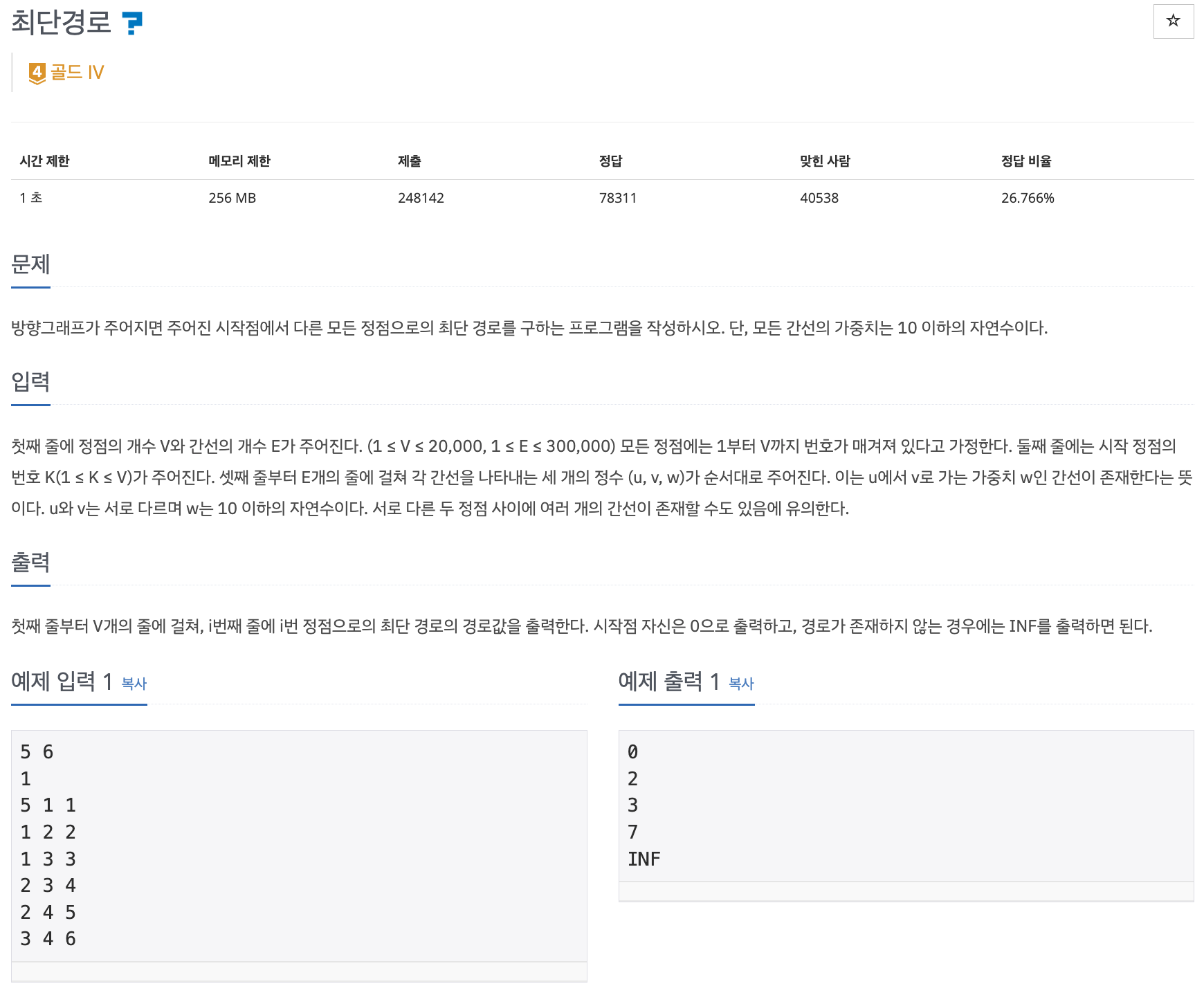
📌 문제 : 백준 1753

📌 문제 탐색하기

V : 정점의 개수 ( $1 ≤ V ≤ 20000$ )
E : 간선의 개수 ( $1 ≤ E ≤ 300000$ )

문제 풀이

시작 정점이 주어졌을 때 이 시작 정점으로부터 각 정점까지의 최단 거리를 구하는 문제이다.

최단 경로는 최소의 가중치를 가질 경우 이동한 경로이므로 가중치있는 최단 거리를 고려할 때 사용하는 다익스트라(힙 활용)를 구현한다.

정해진 시작 정점과 각 정점 간의 모든 최단 경로를 구해 출력하면서 원하는 결과를 얻는다.

가능한 시간복잡도

힙 연산 → $O((V+E)logV)$

최종 시간복잡도
최악일 때 $O((V+E)logV) = O(32000 * log(20000))$ 이 되는데 이는 제한시간 1초 내 충분히 수행 가능하다.

알고리즘 선택

heapq로 다익스트라 구현해 최단 경로 탐색

📌 코드 설계하기

다익스트라 구현
입력받기
경로 비용 저장할 리스트 정의
다익스트라 실행
출력

📌 시도 회차 수정 사항

1회차

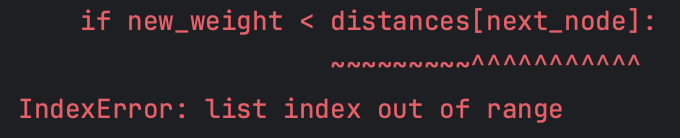
그래프 정보 저장하는 그래프의 크기를 정점 개수만큼 만들어야 하는데 간선 개수만큼 만들어서 IndexError가 발생했다.

2회차

수정했음에도 동일한 에러가 발생했다.
dijkstra 함수의 while문 안에서 새 가중치를 구하고 힙에 넣는 부분에 새롭게 구한 new_weight를 노드와 함께 넣어야 하는데 next_weight를 넣어서 잘못된 결과가 나왔다.

📌 정답 코드

import sys
import heapq

input = sys.stdin.readline
INF = int(1e9)

def dijkstra(start):
    queue = []
    heapq.heappush(queue, (0, start))
    distances[start] = 0

    while queue:
        weight, now_node = heapq.heappop(queue)
        # 더 큰 가중치이면 무시
        if distances[now_node] < weight:
            continue

        for next_node, next_weight in graph[now_node]:
            # 누적 가중치 계산
            new_weight = weight + next_weight
            # 다음 노드의 가중치가 현재보다 작으면 조건 만족
            if new_weight < distances[next_node]:
                distances[next_node] = new_weight
                # 힙 삽입
                heapq.heappush(queue, (new_weight, next_node))


# 입력
V, E = map(int, input().split())
K = int(input())

graph = [[] for _ in range(V+1)]

for _ in range(E):
    u, v, w = map(int, input().split())
    graph[u].append((v, w))

# 최단 경로 저장 리스트 정의
distances = [INF] * (V + 1)

# 다익스트라 실행
dijkstra(K)

# 출력
for i in range(1, V+1):
    if distances[i] == INF:
        print('INF')
    else:
        print(distances[i])