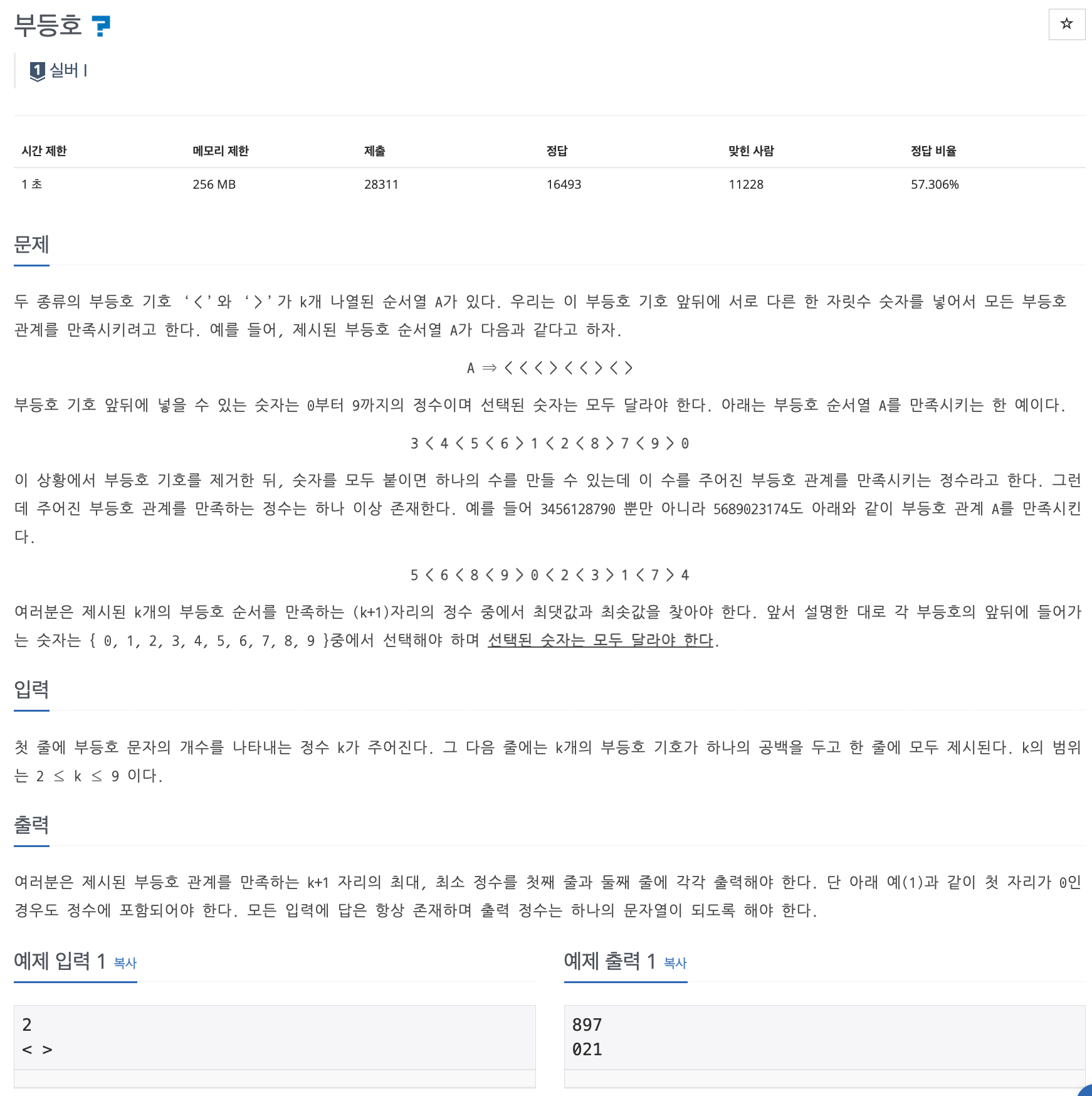
📌 문제 : 백준 2529번
📌 문제 탐색하기
k : 부등호 문자의 개수 ()
A : k개의 부등호가 나열된 순서열
✅ 입력 조건
1.k입력
2.k개의 부등호가 사이에 1개의 공백을 두고 입력
✅ 출력 조건
1. 부등호 관계를 만족하는 k+1 자리의 최대 정수 출력
2. 부등호 관계를 만족하는 k+1 자리의 최소 정수 출력
3. 첫번째 자리의 수가 0인 경우도 포함
4. 출력 정수는 하나의 문자열이 되도록 출력
숫자 { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }중에서 선택해서 입력받은 부등호 관계를 성립하도록 정수를 넣고,
부등호 기호를 모두 제거한 후 모든 정수를 하나의 수로 붙여 만든 k+1자리의 정수 중에서 최댓값과 최솟값을 찾는 문제이다.
{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } 중에서 숫자를 중복되지 않게 선택하면서 k+1자리의 정수들을 모두 만들고, 부등호 조건을 성립하는지 확인한다.
부등호에 대한 조건은 다음과 같다.
<일 때 → 앞 숫자가 뒷 숫자보다 작음>일 때 → 앞 숫자가 뒷 숫자보다 큼
위의 조건을 체크하는 함수를 구현하여 만들어진 숫자가 만족하는지 확인한다.
숫자의 사용 여부를 확인하면서 k+1자리의 정수를 만드는 함수를 구현한다.
{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } 중 k+1개를 선택해 숫자들을 만든다는 아이디어를 통해 순열을 활용한다.
itertools의 permutations으로 만들 수 있는 모든 정수를 만들고,
조건 체크 함수를 통과한 숫자들을 저장한 후 정렬해서 최댓값, 최솟값을 찾아낸다.
가능한 시간복잡도
순열 만들기 →
정렬하기 →
최종 시간복잡도
최악의 경우 k=9일 때, 이다.
이는 1초 내에 연산이 가능하다.
알고리즘 선택
순열을 이용해 만들 수 있는 모든 숫자를 만들고 조건에 해당하는지 체크 후 오름차순 정렬
📌 코드 설계하기
- k 입력
- A 입력
- 부등호 조건 확인하는 함수 구현
- 0 ~ 9 중 k+1개 선택하는 순열 생성해 조건에 맞는 숫자 찾기
- 오름차순 정렬해 최댓값, 최솟값 찾기
📌 시도 회차 수정 사항
1회차
📌 정답 코드
import sys
from itertools import permutations
input = sys.stdin.readline
# 부등호 조건 만족하는지 확인하는 함수
def check_sign(a, b, op):
if op == '<' and a < b:
return True
if op == '>' and a > b:
return True
return False
# k 입력
k = int(input())
# A 입력
A = list(input().rstrip().split())
# 0 ~ 9까지의 정수 리스트 만들기
nums = [i for i in range(10)]
# 새로 만든 정수 저장할 리스트 초기화
new_nums = []
# 0 ~ 9 중 k+1개 선택하는 순열 생성
for per in permutations(nums, k+1):
check = True
for i in range(len(A)):
# 부등호 조건 불만족
if not check_sign(per[i], per[i + 1], A[i]):
check = False
break
# 부등호 조건 만족 시 최댓값, 최솟값 갱신
if check == True:
# 한 문자열로 만들기
n = ''.join(map(str, per))
new_nums.append(n)
# 만들어진 정수 정렬
new_nums.sort()
# 결과 출력
print(new_nums[-1])
print(new_nums[0])
- 결과

📌 회고
- 모든 순열을 생성하는 과정에서 시간이 많이 소요되었다.
k의 범위가 더 컸다면 시간복잡도가 매우 커져서 다른 방법을 찾아야 했을 것이다. - 정수 생성을 DFS를 활용했더니 훨씬 효율적으로 구현할 수 있었다.