[파이썬/Python] 백준 2805번: 나무 자르기

숨·2024년 9월 23일

알고리즘 문제 풀이

목록 보기

83/105

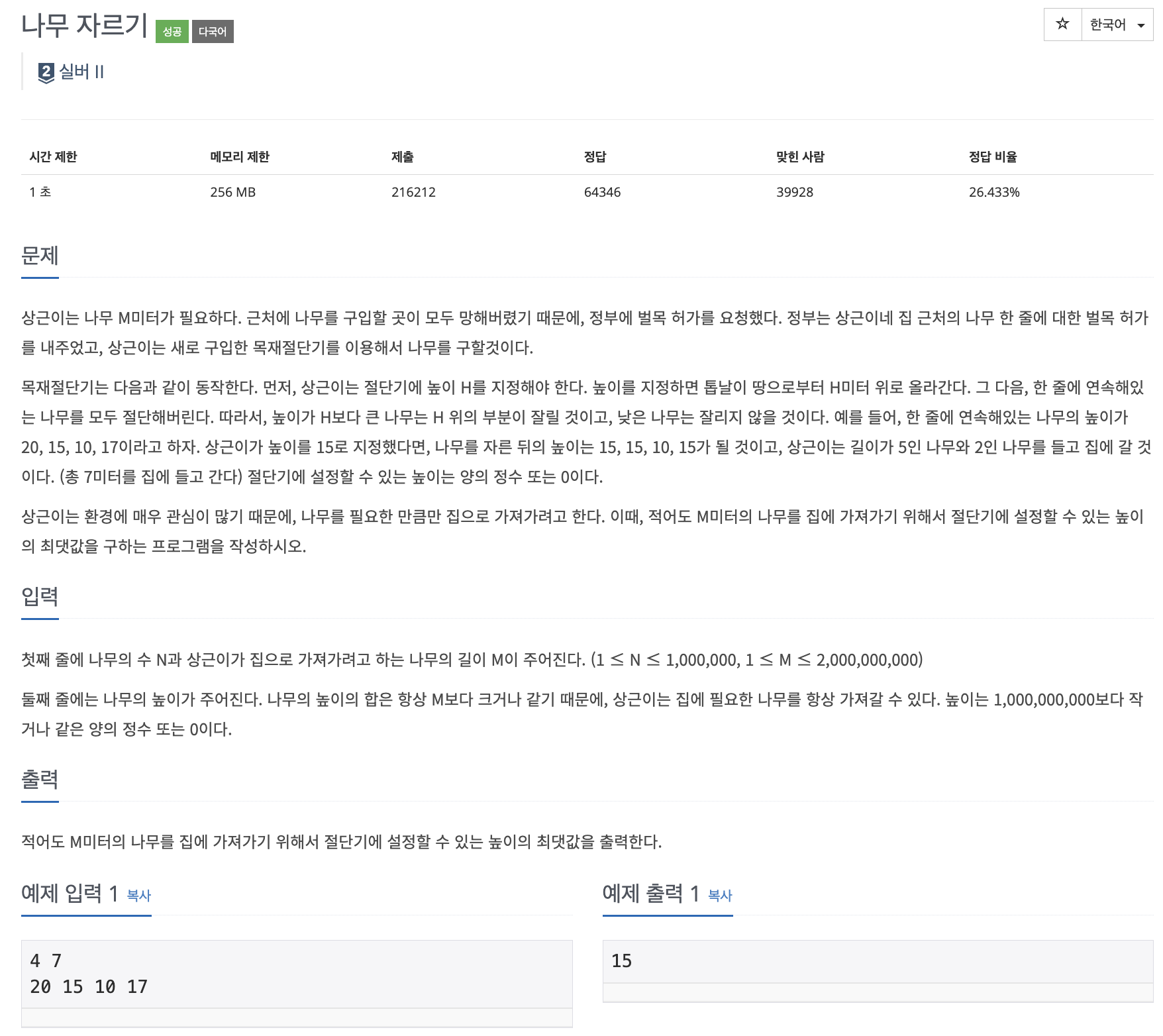
📌 문제 : 백준 2805번

📌 문제 탐색하기

N : 나무의 수 $(1 ≤ N ≤ 1,000,000)$
M : 필요한 나무의 길이 $(1 ≤ M ≤ 2,000,000,000)$
heights : N개의 나무 높이 $(M ≤ sum(heights), 0 ≤ heights ≤ 1,000,000,000)$

N개의 나무를 잘라 최소 M미터 이상 나무를 자르기 위한 절단기의 최대 높이 H를 구하는 문제이다.

문제 풀이

⭐️ 나무 자르는 방법

절단기에 높이 H를 지정한다.

연속해있는 나무 길이 중 H보다 높은 나무들을 자른다.

자른 나무 길이 = 나무 길이 - H

잘린 나무 길이를 모두 합한 값만큼 가져간다.

잘린 나무의 합이 적어도 M인지 확인하면서 절단기 높이를 조절한다.
이를 이분탐색을 통해 구현한다.

🔎 절단기 최대 높이 찾는 이분탐색 구현

탐색 범위 지정

시작점 : 0

끝점 : 나무들 중 높이가 H보다 큰 경우에만 잘라가므로 나무 길이 중 가장 큰 길이로 지정하면 될 것

해당 값을 높이로 했을 때 얻을 수 있는 나무 길이 합을 확인해야 하므로 변수 정의

for문으로 나무 길이 리스트 접근

H보다 큰 경우만 잘린 길이 합산

자른 나무 합에 따라 이분탐색 범위 조정

M보다 크면 H의 최댓값을 구하기 위해 시작점을 더 높여본다.

M보다 작으면 H를 줄여서 더 많은 나무를 얻을 수 있도록 끝점을 줄인다.

가능한 시간복잡도

나무 길이 범위가 매우 크기 때문에 더 주의해야 할 것이다.
0 ~ max(heights) 사이에서 자른 나무 합 계산하며 이분탐색 → $O(N * log(max(heights))$

최종 시간복잡도
$O(N * log(max(heights))$ 로 최악의 경우 $O(1,000,000 * log(max(1,000,000,000))$ 가 되어 약 $O(29,897,353)$ 가 되는데 이는 1초 내 연산 가능하다.

알고리즘 선택

범위 내에서 이분탐색하기

📌 코드 설계하기

필요한 입력 받기
이분탐색 범위 지정
이분탐색 수행
결과 출력

📌 시도 회차 수정 사항

1회차

📌 정답 코드

import sys

input = sys.stdin.readline

# N, M 입력
N, M = map(int, input().split())

# 나무 길이 입력
heights = list(map(int, input().split()))

# 이분탐색 범위 지정
start = 0
end = max(heights)

# 이분탐색 수행
while start <= end:
    # 중앙값 정의
    mid = (start + end) // 2
    # 잘린 나무 길이 합 저장 변수 정의
    cut_trees = 0

    # 잘린 나무 길이 계산
    for height in heights:
        # 절단기 높이보다 높은 나무만 자름
        if height > mid:
            cut_trees += height - mid

    # 합이 적어도 M보다 큰지 확인
    if cut_trees >= M:
        # 크면 최댓값 구하기 위해 절단기 높이를 더 높여본다
        start = mid + 1
    # 합이 M보다 작으면 절단기 높이 더 줄인다
    else:
        end = mid - 1

# 결과 출력
print(end)