[파이썬/Python] 백준 2828번: 사과 담기 게임

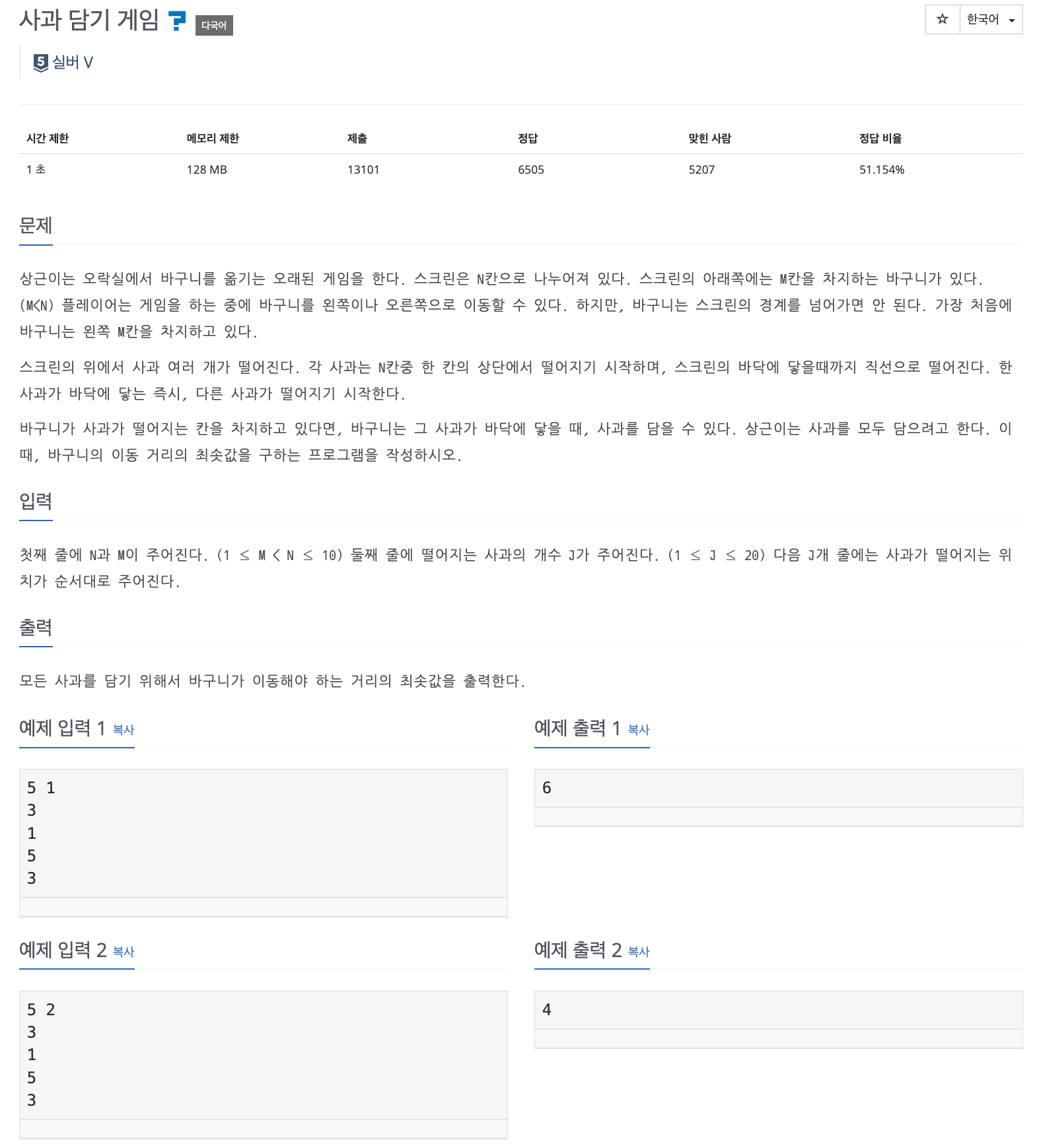
📌 문제 : 백준 2828번

---

📌 문제 탐색하기

N : 스크린 칸 수
M : 바구니 칸 수 (1 ≤ M < N ≤ 10)
J: 떨어지는 사과의 개수 (1 ≤ J ≤ 20)

✅ 입력 조건
1. N과 M이 공백으로 구분되어 입력
2. J 입력
3. J만큼 반복되어 사과가 떨어지는 위치 입력
✅ 출력 조건
1. 모든 사과 담기 위해 바구니가 이동해야 하는 거리의 최솟값 출력

바구니 이동 조건

• 바구니는 왼쪽 또는 오른쪽으로 이동 가능
• 스크린의 경계를 넘어가선 안됨
• 바구니의 초기 위치 : M칸
• 각 사과는 N칸 중 한 칸의 상단에서 떨어지기 시작하고 바닥까지 직선으로 떨어짐
• 1개의 사과가 바닥에 닿으면서 다른 사과가 떨어지기 시작
• 바구니가 사과가 떨어지는 칸에 위치하면 사과 담기 가능

J번의 사과가 떨어질 위치를 리스트로 저장한다.

바구니는 1부터 M까지의 칸을 차지한다.
따라서 바구니의 위치를 왼쪽, 오른쪽 모두 고려해줘야 한다.

만약 사과가 떨어지는 위치가 바구니의 왼쪽 끝보다 작으면 그 차이만큼 이동해야하고, 오른쪽 끝보다 크다면 그 차이만큼 이동해줘야 한다.
바구니의 왼쪽 끝부터 오른쪽 끝부분 내에 사과가 떨어진다면 움직이지 않아도 된다.
이를 고려해서 if문을 작성해준다.

for문을 돌면서 위의 조건에 따라 이동 거리에 더해주면서 계산한다.

가능한 시간복잡도

입력 받기 → $O(1)$
위치 리스트 만들기 → $O(J)$
for 루프에서 연산하기 → $O(J)$

최종 시간복잡도
$O(J)$으로 제한 시간 내에 연산이 가능하다.

알고리즘 선택

for 루프에서 바구니 위치와 사과 떨어지는 위치를 연산하며 누적 이동 거리 구하기.

---

📌 코드 설계하기

1. N M 입력
2. J 입력
3. 사과 떨어지는 위치 J번 입력
4. 바구니의 왼쪽 끝, 오른쪽 끝 위치 정의
5. 이동 거리 누적할 변수 정의
6. for 루프로 사과 떨어지는 위치 반복
7. 3가지 경우 고려
   7-1. 바구니 왼쪽 끝보다 작을 때
   7-2. 바구니 오른쪽 끝보다 클 때
   7-3. 그 사이일 때
8. 원하는 형태로 값 출력

---

📌 시도 회차 수정 사항

1회차

---

📌 정답 코드

import sys

input = sys.stdin.readline

# 1. N M 입력
N, M = map(int, input().split())

# 2. J 입력
J = int(input())

# 3. 사과 떨어지는 위치 J번 입력
locations = [int(input()) for _ in range(J)]

# 4. 바구니의 왼쪽 끝, 오른쪽 끝 위치 정의
left, right = 1, M

# 5. 이동 거리 누적할 변수 정의
move = 0

# 6. for 루프로 사과 떨어지는 위치 반복하며 3가지 경우 고려
for location in locations:
    # 7-1. 바구니 왼쪽 끝보다 작을 때
    if location < left:
        move += left - location
        # 위치 갱신
        left = location
        right = location + M - 1

    # 7-2. 바구니 오른쪽 끝보다 클 때
    elif location > right:
        move += location - right
        # 위치 갱신
        left = location - M + 1
        right = location

    # 7-3. 그 사이일 때
    else:
        move += 0

# 8. 원하는 형태로 값 출력
print(move)import sys

input = sys.stdin.readline

# 1. N M 입력
N, M = map(int, input().split())

# 2. J 입력
J = int(input())

# 3. 사과 떨어지는 위치 J번 입력
locations = [int(input()) for _ in range(J)]

# 4. 바구니의 왼쪽 끝, 오른쪽 끝 위치 정의
left, right = 1, M

# 5. 이동 거리 누적할 변수 정의
move = 0

# 6. for 루프로 사과 떨어지는 위치 반복하며 3가지 경우 고려
for location in locations:
    # 7-1. 바구니 왼쪽 끝보다 작을 때
    if location < left:
        move += left - location
        # 위치 갱신
        left = location
        right = location + M - 1

    # 7-2. 바구니 오른쪽 끝보다 클 때
    elif location > right:
        move += location - right
        # 위치 갱신
        left = location - M + 1
        right = location

    # 7-3. 그 사이일 때
    else:
        move += 0

# 8. 원하는 형태로 값 출력
print(move)

• 결과
  

---

📌 회고

for location in locations:
    temp = M
    move += abs(location - M)
    M = location

• 처음엔 M이 바구니 위치의 초기값을 의미하는 줄 알고 위와 같이 단순 연산으로 코드를 작성했다. 2번째 예제를 적용해보면서 문제를 제대로 파악할 수 있었다. 문제 파악의 중요성을 다시 깨달았다.

---

# 7-1. 바구니 왼쪽 끝보다 작을 때
if location < left:
    move += left - location
    # 위치 갱신
    left = location
    right = location + M

# 7-2. 바구니 오른쪽 끝보다 클 때
elif location > right:
    move += location - right
    # 위치 갱신
    left = location - M
    right = location

• left, right를 location에 M을 더하고 빼는 형태로 갱신했는데 1이 덜 가거나 더 간 위치로 갱신되었다. 따라서 아래와 같이 1을 빼고 더해주는 과정을 추가해서 코드를 수정하였다.

# 7-1. 바구니 왼쪽 끝보다 작을 때
if location < left:
    move += left - location
    # 위치 갱신
    left = location
    right = location + M - 1

# 7-2. 바구니 오른쪽 끝보다 클 때
elif location > right:
    move += location - right
    # 위치 갱신
    left = location - M + 1
    right = location