[파이썬/Python] 백준 8895번: 막대 배치

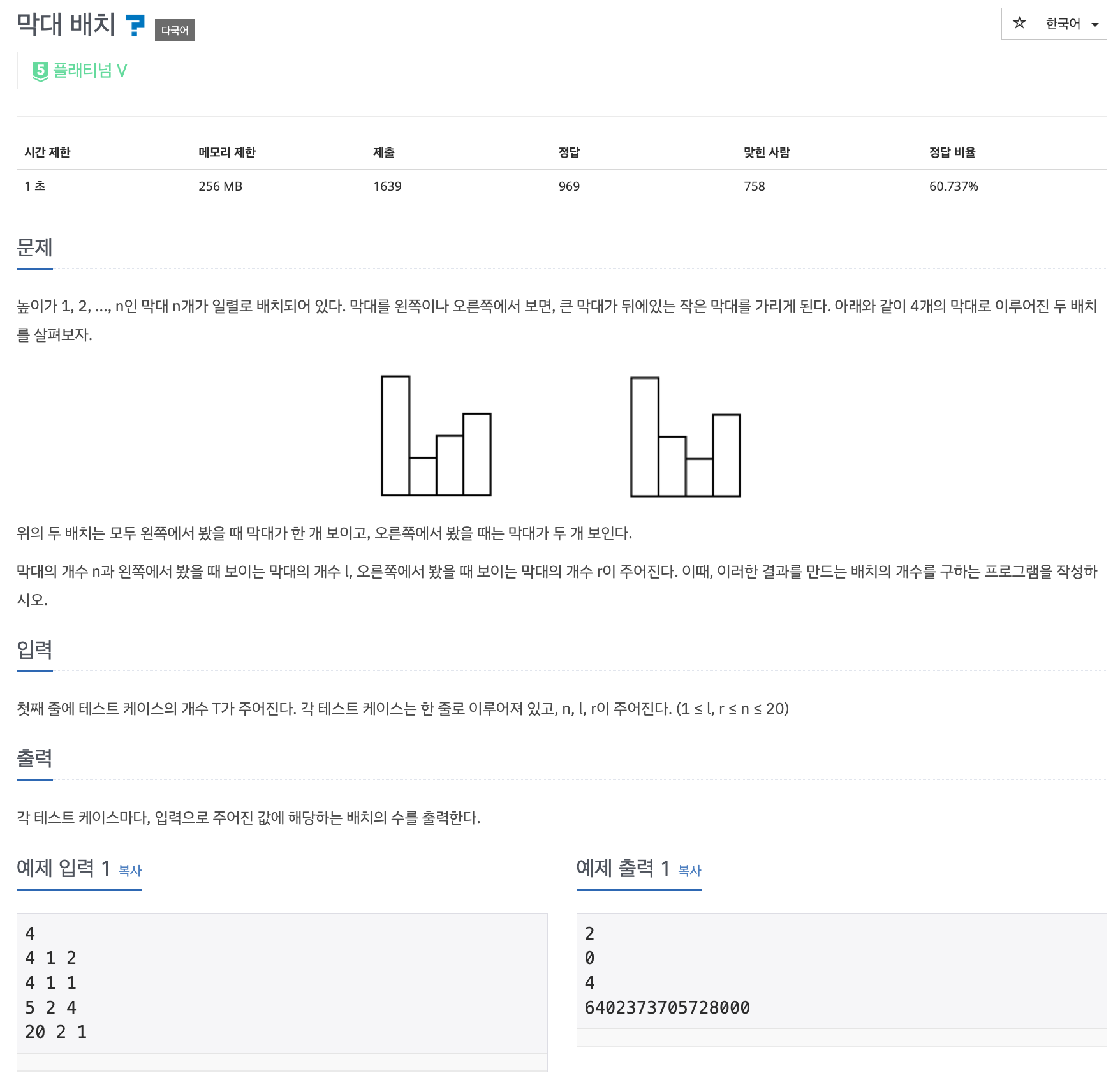
📌 문제 : 백준 8895번

---

📌 문제 탐색하기

T : 테스트케이스 수
n : 막대 개수 ($1 ≤ l, r ≤ n ≤ 20$)
l : 왼쪽에서 보이는 막대 개수
r : 오른쪽에서 보이는 막대 개수

문제 풀이

각 테스트케이스마다, 막대가 n개 있을 때 왼쪽에서 l개, 오른쪽에서 r개 보이는 막대 배치의 개수를 구하는 문제이다.

보이는 막대의 개수는 가장 큰 막대에 영향을 받는다.

• 가장 큰 막대의 배치 위치
  • 맨 왼쪽 → 왼쪽에서 보는 막대 1개
  • 맨 오른쪽 → 오른쪽에서 보는 막대 1개
  • 막대 배치 위치가 맨 왼쪽, 맨 오른쪽, 그외에 따라 결과 달라짐

따라서 가장 큰 막대부터 작은 막대 순서로 배치한다고 생각한다.

현 상황에서 가장 작은 막대를 어디에 놓는지에 따라 보이는 막대 수를 조절하는 식으로 점화식을 작성할 수 있을 것이다.
→ 이전의 배치 수에 현재 놓을 수 있는 경우의 수를 더해서 구할 수 있기 때문!

이 문제를 풀기 위해서 이용해야 할 상태는 지금 몇개의 막대를 배치했는지, 현재 왼쪽에서 보이는 막대 개수, 오른쪽에서 보이는 막대 개수로 3가지이다.

⭐️ 가장 작은 막대 배치 상황

• 맨 왼쪽
  • 막대 1개 적은 경우보다 왼쪽에서 보이는 막대 개수 1 🔺
• 맨 오른쪽
  • 막대 1개 적은 경우보다 오른쪽에서 보이는 막대 개수 1 🔺
• 중간 어딘가
  • 보이는 막대수 유지
  • n-2개의 위치 존재

위의 경우에 따라 다이나믹 프로그래밍 알고리즘으로 풀기 위한 점화식을 세울 수 있다.

dp[n][l][r]을 n개 배치한 상황에서 왼쪽 l개, 오른쪽 r개 보이는 막대의 배치 경우의 수라고 한다면 점화식은 다음과 같다.

• 왼쪽 : dp[n][l][r] += dp[n-1][l-1][r]
• 오른쪽 : dp[n][l][r] += dp[n-1][l][r-1]
• 왼쪽, 오른쪽 제외 : dp[n][l][r] += dp[n-1][l][r] * (n-2)

위 점화식으로 문제를 풀기 위해 먼저 dp 테이블을 정의해준다.

dp 테이블 정의

• l, r, n 모두 최대 20 → $20^3$ 크기로 정의해 0으로 채움
• l=1, r=1, n=1일 때 경우의 수 1 → dp 테이블 초기화

dp 테이블 채우기

• 3중 for문 이용
  • 첫번째 for문
    • 초기화했기 때문에 n은 인덱스 2부터 20까지 진행
  • 두번째 for문 → 1부터 입력받은 l까지
  • 세번째 for문 → 1부터 입력받은 r까지

가능한 시간복잡도

dp 테이블 채우기 → $O(n * l * r)$

최종 시간복잡도
n, l, r 모두 최대 20이므로 $O(20^3)$이 되어 제한 시간 1초 내에 연산이 가능하다.

알고리즘 선택

점화식을 이용한 dp 테이블 계산

---

📌 코드 설계하기

1. 테스트케이스 입력
2. 테스트케이스마다 반복
3. dp 테이블 정의
4. dp 테이블 초기화
5. dp 테이블 채우기
6. 결과 출력

---

📌 시도 회차 수정 사항

1회차

---

📌 정답 코드

import sys

input = sys.stdin.readline

# 테스트케이스 입력
T = int(input())

# 테스트케이스마다 반복
for _ in range(T):
    # n, l, r 입력
    n, l, r = map(int, input().split())

    # dp 테이블 정의
    dp = [[[0 for _ in range(21)] for _ in range(21)] for _ in range(21)]

    # dp 테이블 초기화
    dp[1][1][1] = 1

    # dp 테이블 채우기
    for i in range(2, 21):
        for j in range(1, l + 1):
            for k in range(1, r + 1):
                dp[i][j][k] += dp[i-1][j-1][k]
                dp[i][j][k] += dp[i - 1][j][k - 1]
                dp[i][j][k] += dp[i - 1][j][k] * (i - 2)

    # 결과 출력
    print(dp[n][l][r])

• 결과