📌 문제 : 프로그래머스 - 땅따먹기
📌 문제 탐색하기
N : 행의 개수 ()
scores : 점수 ()
문제 풀이
총 N행 4열로 이루어진 땅(land)의 각 칸에 점수가 쓰여 있다.
1행부터 N행까지 내려오면서 각 행의 4칸 중 한 칸만 밟으면서 내려왔을 때 얻을 수 있는 점수의 최댓값을 구하는 문제이다.
단, 같은 열을 연속으로 밟을 수 없다는 규칙이 존재한다.
이 문제는 현재 행의 각 칸에 올 수 있는 최대 점수를 구하는 문제로, 이전 행에서 같은 열이 아닌 칸 중 최댓값과 현재 행의 최대 점수를 더함으로써 구할 수 있다.
→ 이전의 계산 결과를 이용하는 Dynamic Programming(동적 계획법)으로 해결한다.
📖 Dynamic Programming(DP, 동적 계획법)
- 한 번 해결된 부분 문제의 정답을 메모리에 기록 → 다시 계산하지 않도록 하는 문제 해결 기법
- 점화식을 그대로 코드로 옮겨서 구현
- 점화식 : 인접한 항들 사이의 관계식 의미
- 코드 작성 방법
- 탑다운 방식(Top-Down, 메모이제이션, 하향식)
- 재귀 함수로 큰 문제 해결 위해 작은 문제 호출
- 보텀업 방식(Bottom-Up, 상향식)
- 단순 반복문으로 해결된 작은 문제 모아 큰 문제 해결
입력받은 land 배열 자체를 DP 테이블로 재사용한다.
첫번째 행에서는 계산될 부분이 없으므로 DP 계산은 두번째 행부터 진행한다.
land[i][j]는 i번째 행의 j열을 밟고 내려왔을 때 얻을 수 있는 최대 점수를 의미한다.
이 점수는 바로 윗행 i-1에서 j열 외의 열의 값들을 통해 구할 수 있으므로 land[i-1][:j] + land[i-1][j+1:]로 j열이 제외된 3칸의 리스트를 만들고 그 중 가장 큰 값을 더해서 구해진다.
이 과정을 반복하면 최종적으로 land 배열의 마지막 칸에 최댓값이 저장된다.
가능한 시간복잡도
N개의 행에 대해 DP →
최종 시간복잡도
최악일 때 이 되는데 이는 충분히 수행 가능하다.
알고리즘 선택
- 최댓값을 누적해서 구하는 DP 활용
📌 코드 설계하기
- 입력받은 배열을 DP 테이블화
- 반복문을 통해 DP 계산
- 정답 반환
📌 시도 회차 수정 사항
1회차
📌 정답 코드
def solution(land):
N = len(land)
for i in range(1, N):
for j in range(4):
land[i][j] += max(land[i-1][:j] + land[i-1][j+1:])
return max(land[-1])
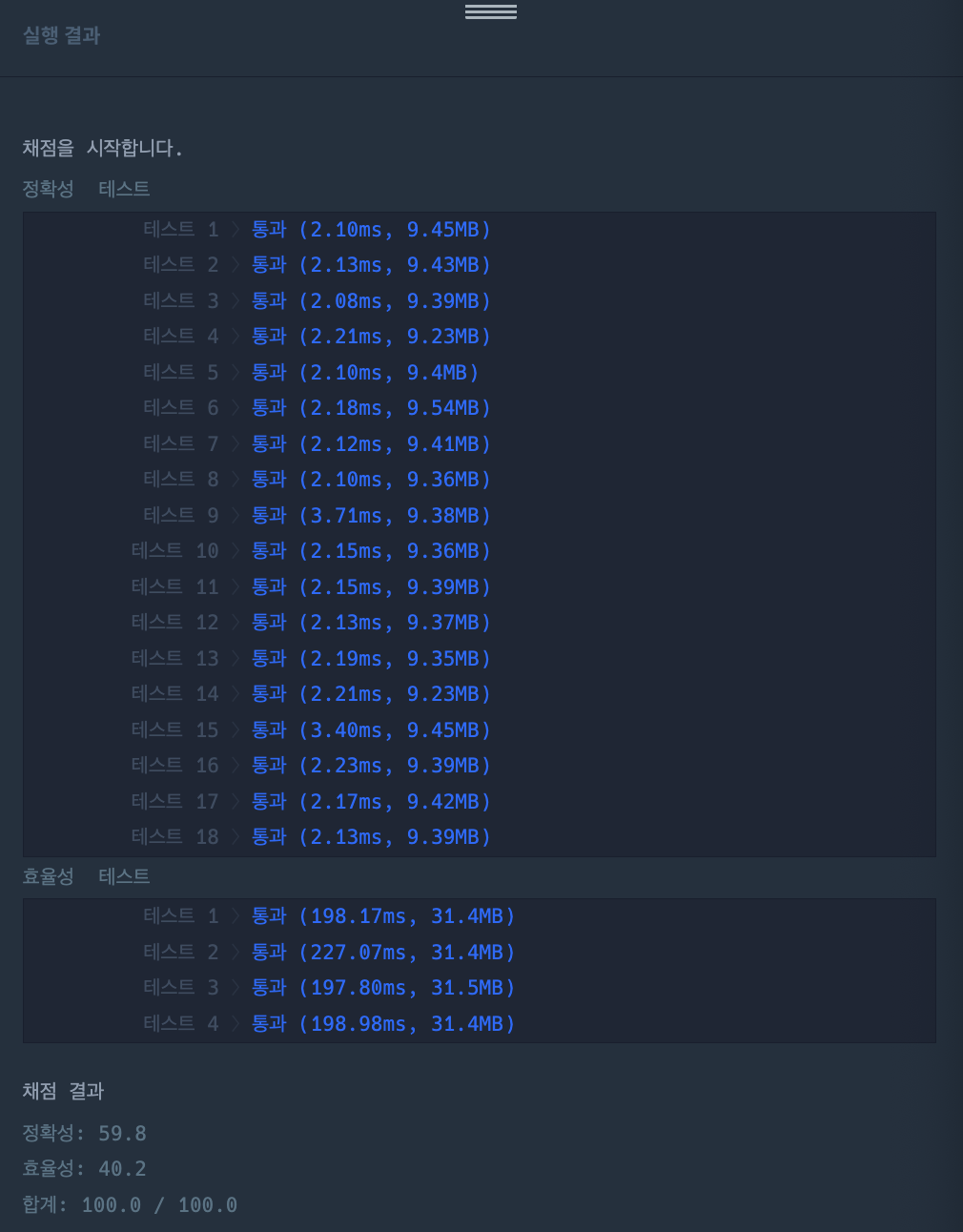
- 결과
✏️ 회고
- DP 문제를 완전히 까먹었다. 규칙을 찾아내는 것에 익숙해져야 하는데 오랫동안 안풀었더니 이렇게 되었다..