선형탐색

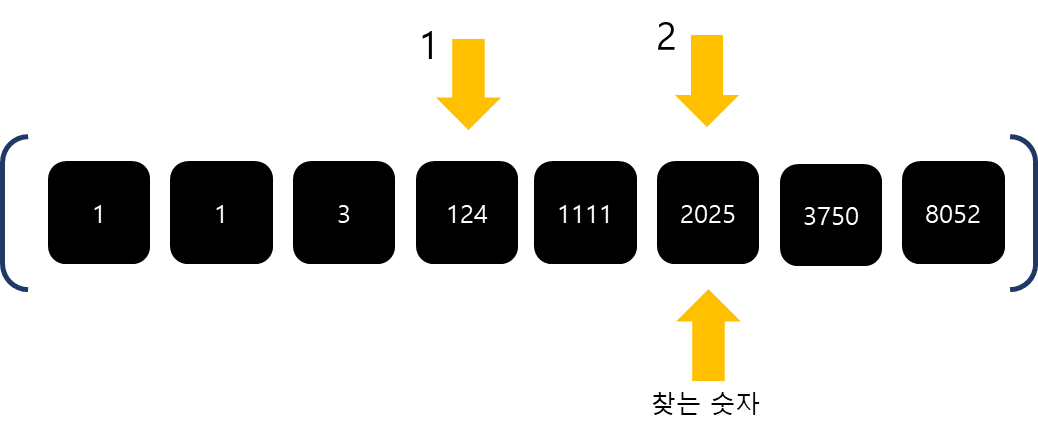
선형탐색은 순서대로 하나씩 찾는 탐색 알고리즘입니다.
따라서 O(n)의 시간복잡도를 갖습니다.

이진 탐색

정렬 되어있는 요소들을 반씩 제외하며 찾는 알고리즘입니다.
O(logn)의 시간복잡도를 갖습니다.

이진 탐색의 특징

• 반드시 정렬이 되어있어야 한다. 정렬이 되어있지 않으면 정렬을 진행해야하기 때문에
  그만큼 시간복잡도를 추가를 갖는다.
• 배열 혹은 이진 트리를 이용하여 구현가능하다.
• O(logn)의 시간복잡도를 갖는다.

13을 찾기 위해서는?
Left, Mid, Right을 설정합니다.
Left는 첫번째 값, Right는 마지막 값, Mid는 중간값입니다.

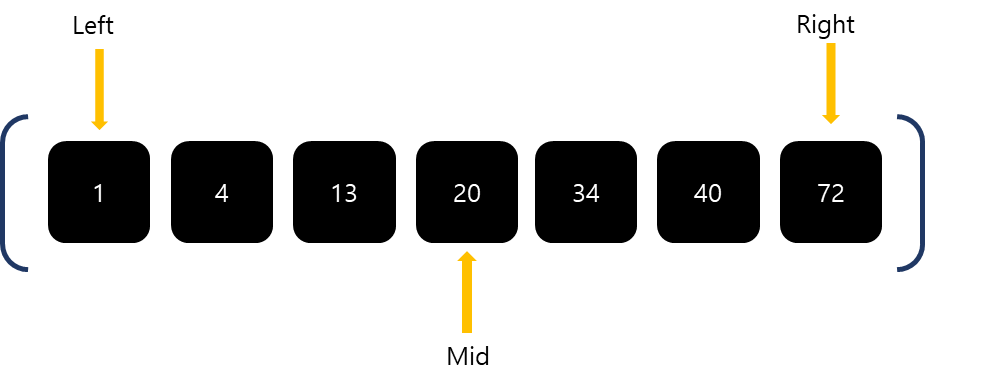
찾고자하는 13과 Mid를 비교합니다.

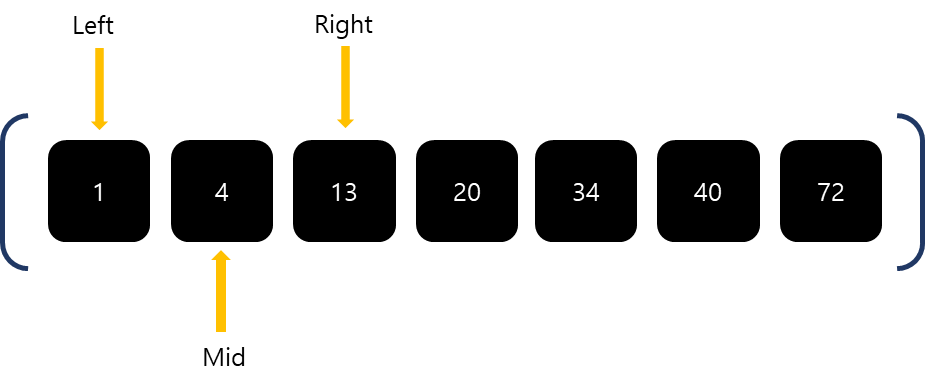
Mid(20)보다 13이 작기때문에 Right의 값을 Mid의 왼쪽으로 한칸 이동시킵니다.
다시 Mid(4)를 설정합니다.

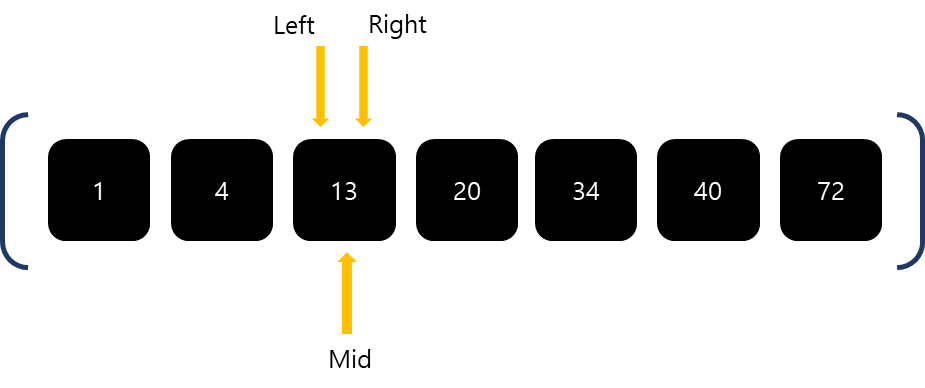
4보다 13이 더 크기때문에 Left를 Mid의 오른쪽으로 한칸 이동시킵니다.
Mid와 13이 같아졌습니다. 탐색을 종료합니다.

배열을 이요한 방법은 중간에 요소를 추가하거나 삭제할때 여전히 O(n)의 시간복잡도를 갖습니다.

이진 탐색 트리

이진 탐색을 위한 이진 트리로 왼족 서브 트리는 루트보다 작은 값이 모여있고
오른쪽 서브 트리는 루트보다 큰 값이 모여있습니다.

요소 추가

5, 4, 7, 8, 5, 6, 2를 순서대로 추가

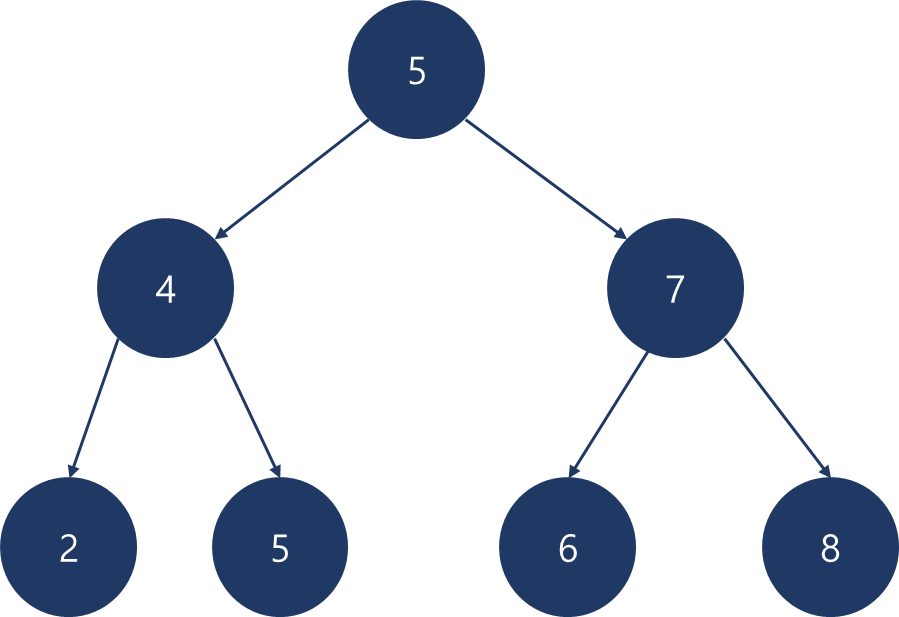
1. 5 추가 (루트에 설정)
2. 4 추가 (루트보다 작음) -> (왼쪽에 위치)
3. 7 추가 (루트보다 큼) -> (오른쪽에 위치)
4. 8 추가 (루트보다 큼) -> (오른쪽에 위치) -> (7보다 큼) -> (오른쪽)
5. 5 추가 (루트와 같음) -> (왼쪽/오른쪽에 위치) -> (4보다 큼) -> (오른쪽)
6. 6 추가 (루트보다 큼) -> (오른쪽에 위치) -> (7보다 작음) -> (왼쪽)
7. 2 추가 (루트보다 작음) -> (왼쪽에 위치) -> (4보다 작음) -> (왼쪽)

요소 삭제

이진트리의 요소 삭제는 별다른 처리없이 부모 정점과의 연결을 끊으면 됩니다.

하나의 서브 트리를 가지는 경우

7을 제거시 root의 오른쪽 간선을 8을 향하도록합니다.

두 개의 서브 트리를 가지는 경우

왼쪽 서브 트리의 가장 큰 값 혹은 오른쪽 서브 트리의 가장 작은 값과 교체합니다.
ex) 4을 제거시 5가 정점이 됩니다.

문제점

5, 4, 3, 2를 추가하게되면 추가되는 값은 항상 각 정점보다 작기때문에
왼쪽으로 편향된 트리가 됩니다.

이러한 경우 순차 탐색과 동일한 시간복잡도를 가지게되고 이를 해결하기 위해
다음 자료구조를 이용할 수 있다.

• AVL 트리
• 레드-블랙 트리

JavaScript 구현

배열

const array = [1, 2, 5, 124, 400, 599, 1004, 2876, 8712];

function binarySearch(array, findValue) {
  let left = 0;
  let right = array.length - 1;
  let mid = Math.floor((left + right) / 2);

  while (left <= right) {
    if (array[mid] === findValue) {
      return mid;
    }

    if (array[mid] < findValue) {
      left = mid + 1;
    } else {
      right = mid - 1;
    }

    mid = Math.floor((left + right) / 2);
  }

  return -1;
}

console.log(binarySearch(array, 2876)); // 7
console.log(binarySearch(array, 1)); // 0
console.log(binarySearch(array, 500)); // -1

이진 탐색 트리

기존 이진 트리에 탐색 함수만 추가하면 됩니다.

// -------- 기존 이진 트리 ----------------
class Node {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  constructor() {
    this.root = null;
  }

  insert(value) {
    const newNode = new Node(value);
    if (this.root === null) {
      this.root = newNode;
      return;
    }

    let currNode = this.root;
    while (currNode !== null) {
      if (currNode.value < value) {
        if (currNode.right === null) {
          currNode.right = newNode;
          break;
        }
        currNode = currNode.right;
      } else {
        if (currNode.left === null) {
          currNode.left = newNode;
          break;
        }
        currNode = currNode.left;
      }
    }
  }
//-------- 탐색 함수 ----------------
  has(value) {
    let currNode = this.root;
    while (currNode !== null) {
      if (currNode.value === value) {
        return true;
      }

      if (currNode.value < value) {
        currNode = currNode.right;
      } else {
        currNode = currNode.left;
      }
    }

    return false;
  }
}

const tree = new BinarySearchTree();
tree.insert(5);
tree.insert(4);
tree.insert(7);
tree.insert(8);
tree.insert(5);
tree.insert(6);
tree.insert(2);

console.log(tree.has(5)); // true
console.log(tree.has(1)); // false