문제

백준 1260번
https://www.acmicpc.net/problem/1260

그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.

첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.

첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.

• 예시
  

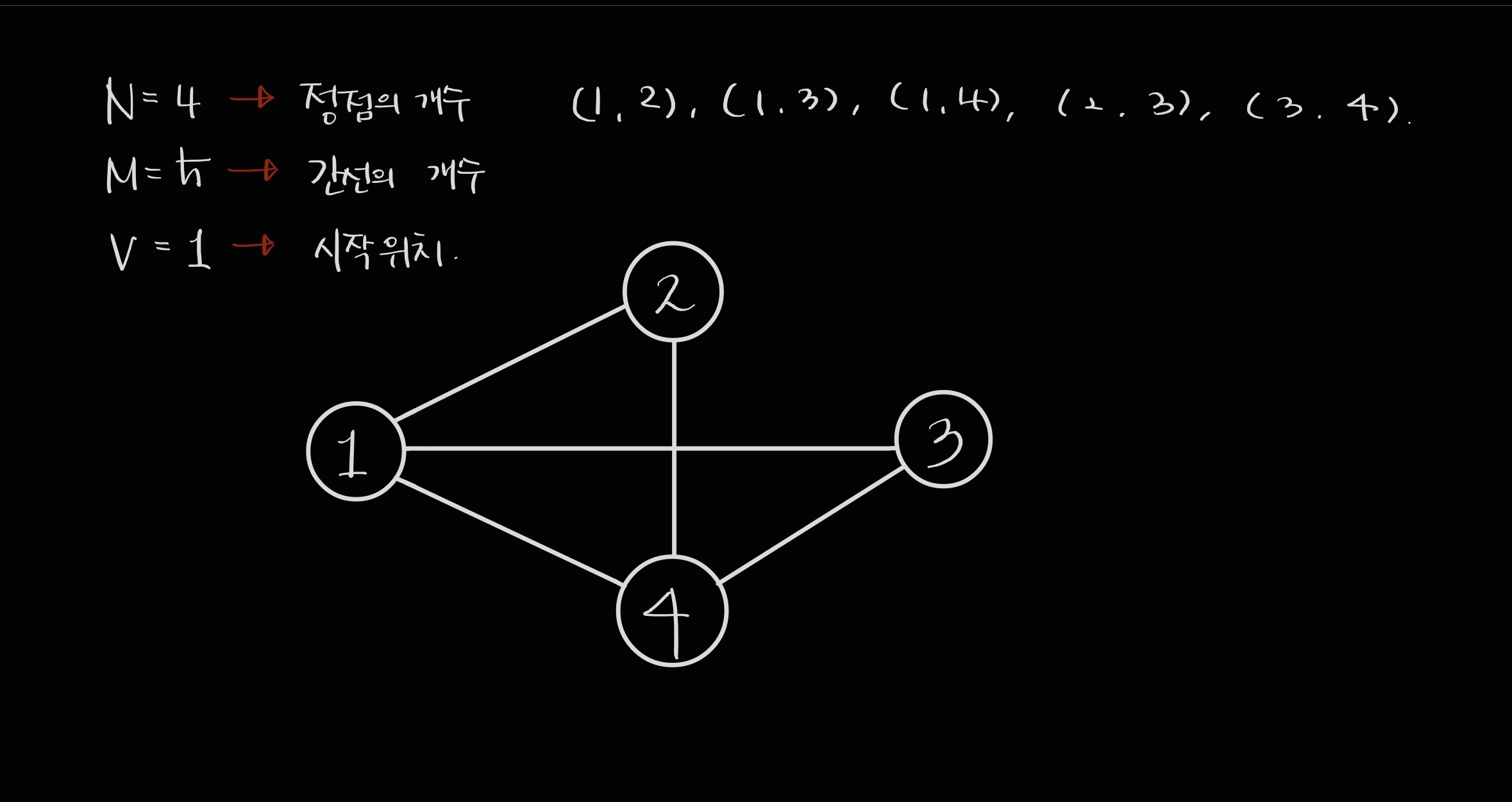
• 1번 예시를 표현한 것
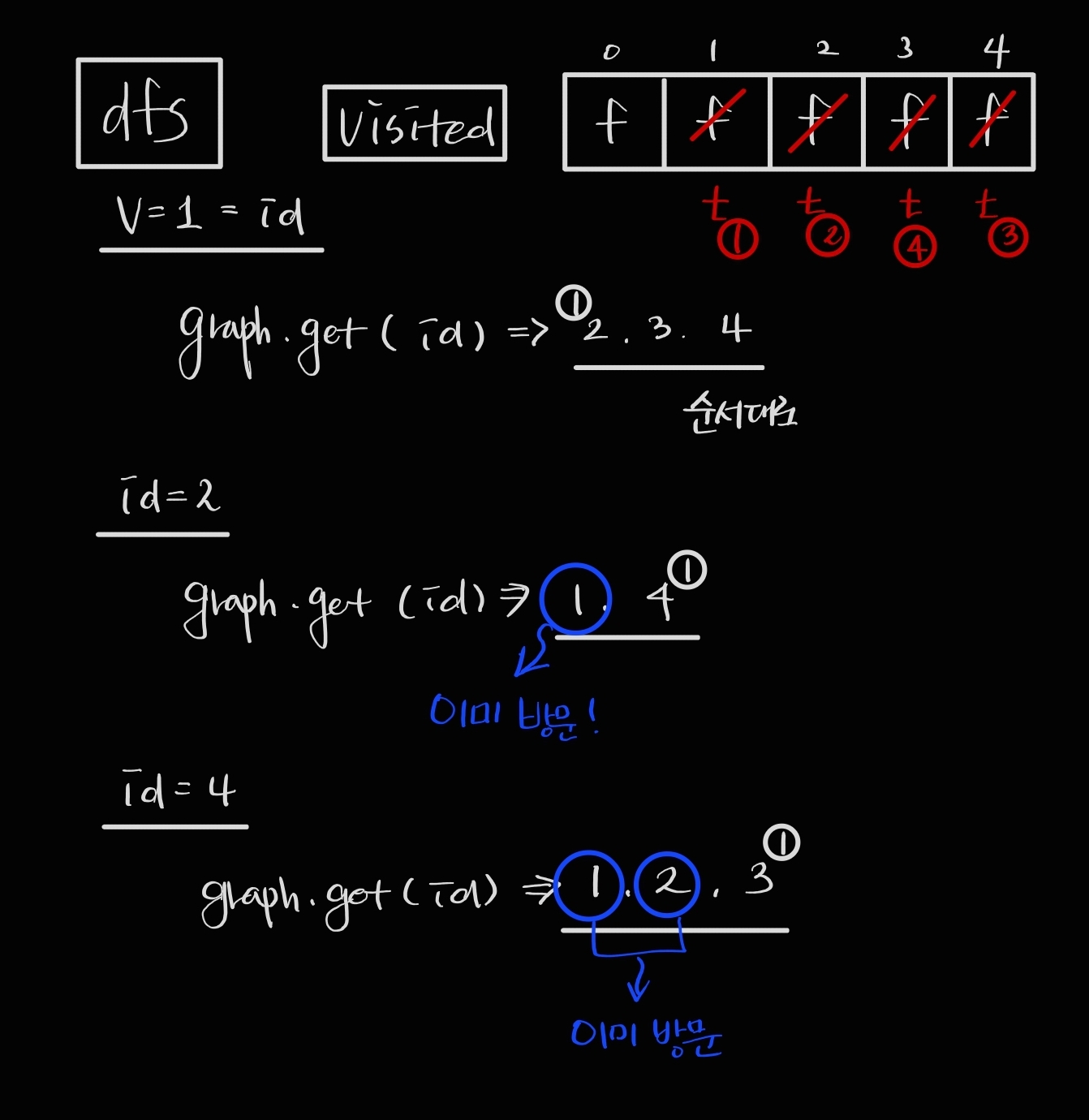
  • DFS 탐색
    • 시작위치가 1이므로 1 방문
    • 1에서 연결된 정점 중 정점 번호가 작은 정점인 2 방문
    • 2에서 방문하지 않은 정점 중 정점 번호가 작은 정점인 4 방문
    • 4에서 방문하지 않은 정점 중 정점 번호가 작은 정점인 3 방문
    • 최종적으로 1 - 2 - 4 - 3
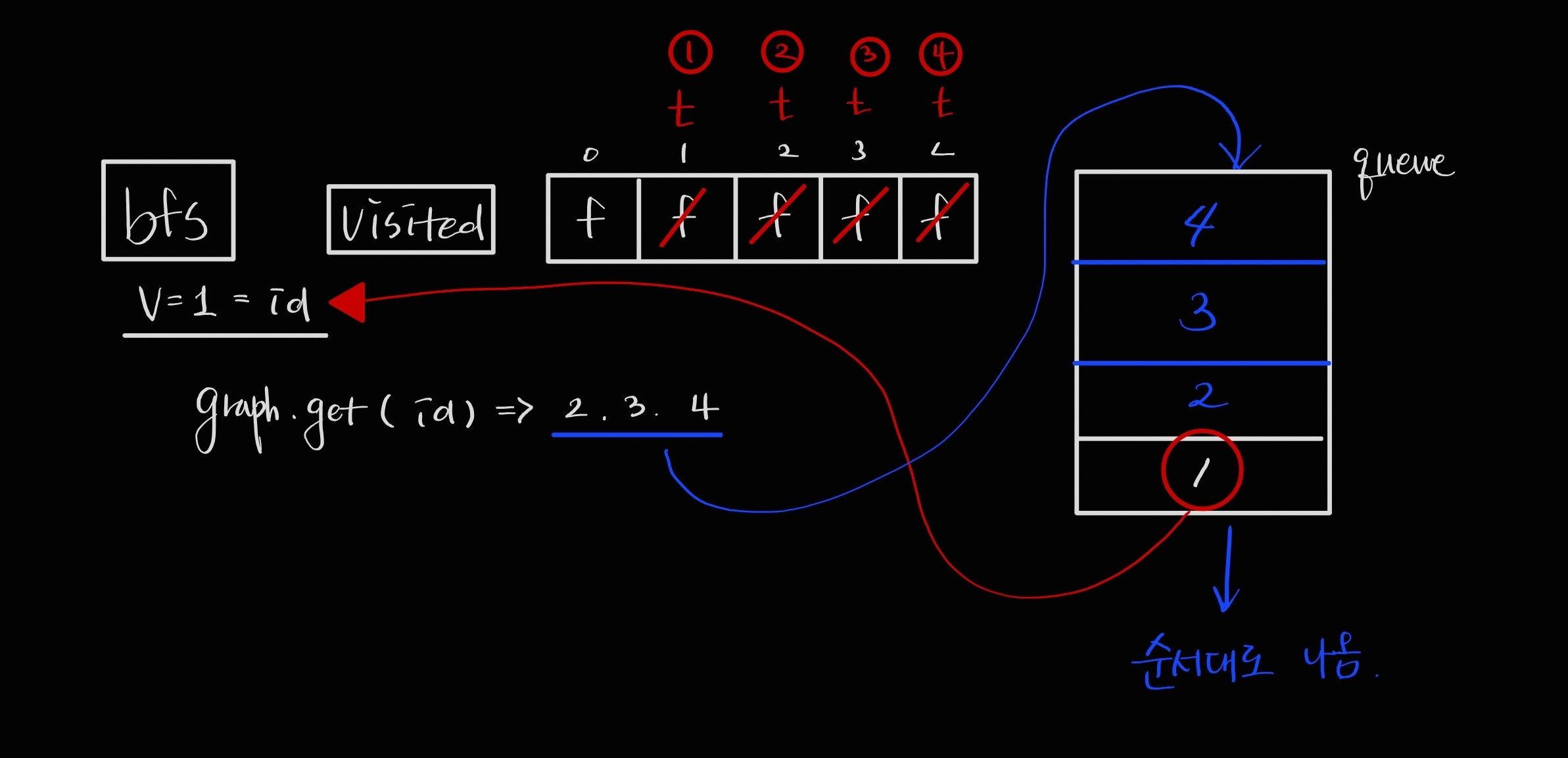
  • BFS 탐색
    - 시작위치가 1이므로 1 방문
    • 1에서 연결된 정점 중 정점 번호가 작은 정점인 2 방문
    • 1에서 연결된 정점 중 정점 번호가 작은 정점인 3 방문
    • 1에서 연결된 정점 중 정점 번호가 작은 정점인 4 방문
    • 최종적으로 1 - 2 - 3 - 4

Code

• DFS는 재귀 호출 구현과 Stack 구현 두 가지로 나타낼 수 있다.
  • 재귀 호출로 구현할 시 코드의 길이를 줄이고 간편하게 구현할 수 있다.
• BFS는 Queue 구현으로 나타낼 수 있다.

BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); // 정점의 개수
int M = Integer.parseInt(st.nextToken()); // 간선의 개수
int V = Integer.parseInt(st.nextToken()); // 시작 번호

graph = new ArrayList<>();
for (int i = 0; i < N + 1; i++) {
        graph.add(new ArrayList<>());
}

for (int i = 0; i < M; i++) {
    st = new StringTokenizer(br.readLine());
    int from = Integer.parseInt(st.nextToken()); // from 정점
    int to = Integer.parseInt(st.nextToken());  // to 정점
    // 양방향 연결
    graph.get(from).add(to);
    graph.get(to).add(from);
}

for (int i = 0; i < N + 1; i++) {
	// 정점 번호가 작은 것을 먼저 방문하기 위해 정렬
	Collections.sort(graph.get(i));
}

boolean[] visited = new boolean[N + 1]; 
dfs(N, visited, V);
// DFS메서드
public static void dfs(int N, boolean[] visited, int id) {
    visited[id] = true;

    sb.append(id).append(" ");

    for (int idx : graph.get(id)) {
        if (!visited[idx]) {
            dfs(N, visited, idx); // 재귀 호출
        }
    }
}

visited = new boolean[N + 1];
bfs(N, visited, V);
// BFS메서드
public static void bfs(int N, boolean[] visited, int id) {
    Queue<Integer> queue = new LinkedList<>();

    queue.offer(id);
    visited[id] = true;

    while (!queue.isEmpty()) {
        int curId = queue.poll();
        sb.append(curId).append(" ");

        for (int i = 0; i < graph.get(curId).size(); i++) {
            int temp = graph.get(curId).get(i);

            if (!visited[temp]) {
                visited[temp] = true;
                queue.offer(temp);
            }
        }
    }
}

Java

import java.io.*;
import java.util.*;

public class Main {
    static List<ArrayList<Integer>> graph;
    static StringBuilder sb = new StringBuilder();
    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken()); // 정점의 개수
        int M = Integer.parseInt(st.nextToken()); // 간선의 개수
        int V = Integer.parseInt(st.nextToken()); // 시작 번호

        graph = new ArrayList<>();
        for (int i = 0; i < N + 1; i++) {
            graph.add(new ArrayList<>());
        }

        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            int from = Integer.parseInt(st.nextToken()); // from 정점
            int to = Integer.parseInt(st.nextToken());  // to 정점
            // 양방향 연결
            graph.get(from).add(to);
            graph.get(to).add(from);
        }

        for (int i = 0; i < N + 1; i++) {
        	// 정점 번호가 작은 것을 먼저 방문하기 위해 정렬
            Collections.sort(graph.get(i));
        }

		// dfs 방문 확인
        boolean[] visited = new boolean[N + 1];
        dfs(N, visited, V);
        // bfs 방문 확인
        visited = new boolean[N + 1];
        sb.append("\n");
        bfs(N, visited, V);
        System.out.println(sb.toString());
    }

    public static void dfs(int N, boolean[] visited, int id) {
        visited[id] = true;

        sb.append(id).append(" ");

        for (int idx : graph.get(id)) {
            if (!visited[idx]) {
                dfs(N, visited, idx); // 재귀 호출
            }
        }
    }

    public static void bfs(int N, boolean[] visited, int id) {
        Queue<Integer> queue = new LinkedList<>();

        queue.offer(id);
        visited[id] = true;

        while (!queue.isEmpty()) {
            int curId = queue.poll();
            sb.append(curId).append(" ");

            for (int i = 0; i < graph.get(curId).size(); i++) {
                int temp = graph.get(curId).get(i);

                if (!visited[temp]) {
                    visited[temp] = true;
                    queue.offer(temp);
                }
            }
        }
    }
}