algorithm - 이코테(swift)

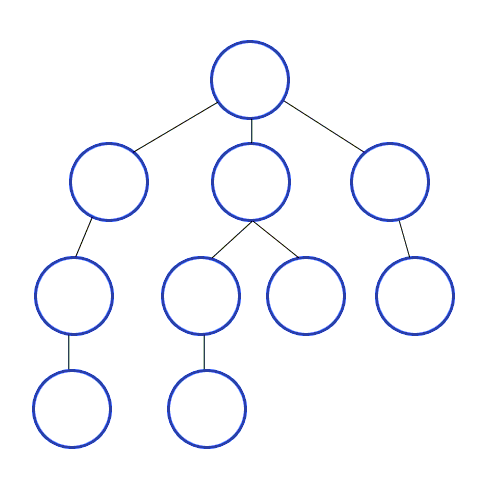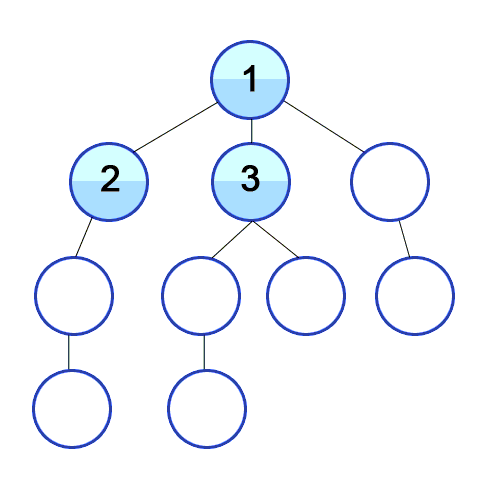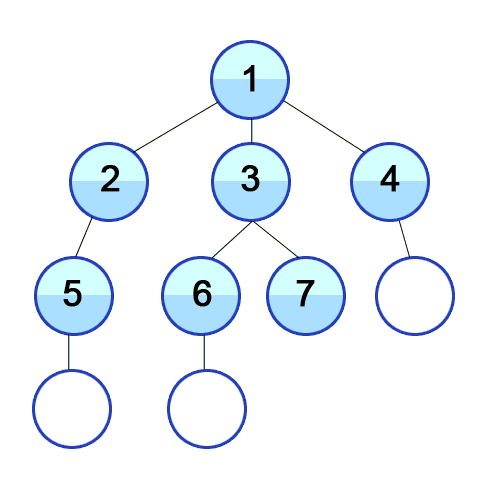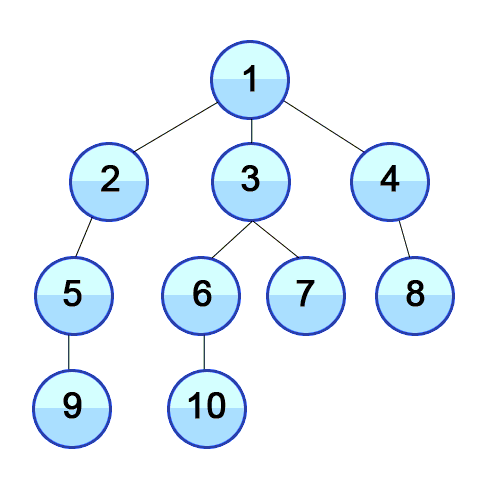
1. DFS (깊이 우선 탐색 - Depth-First Search)

• 최대한 깊이 내려간 뒤, 더 이상 깊이 갈 곳이 없을 경우 옆으로 이동
• 미로찾기를 할 때 최대한 한 방향으로 갈 수 있을 때까지 쭉 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 그 갈림길부터 다시 다른 방향으로 탐색을 진행하는 것
• 스택 또는 재귀함수로 구현
  

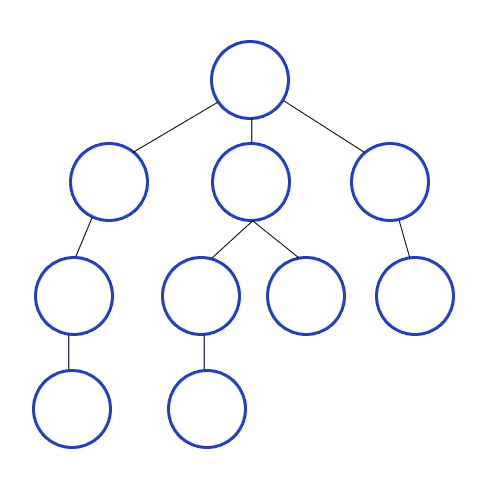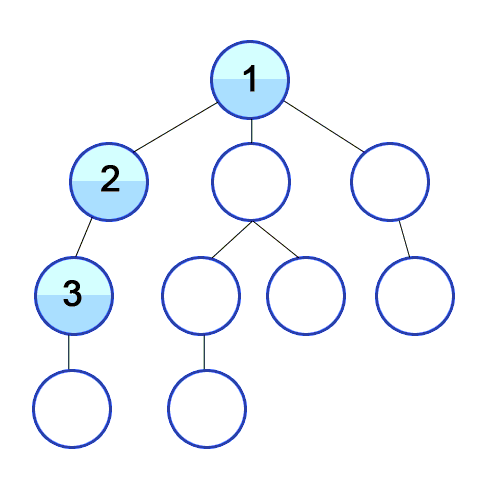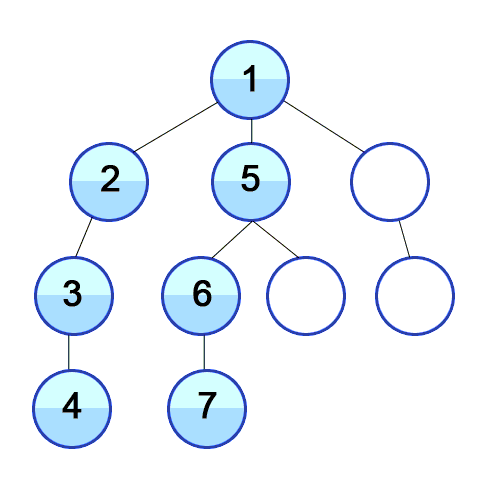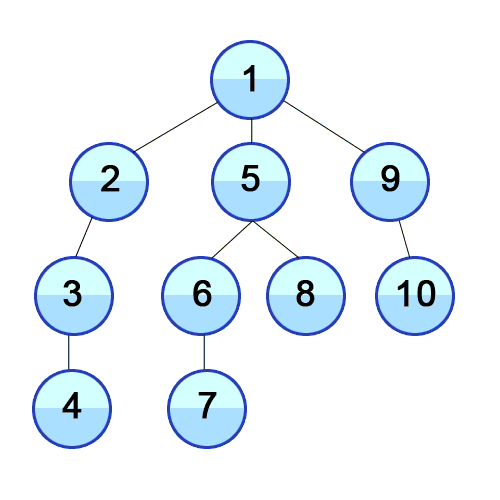
let graph: [[Int]] = [[], [2, 5, 9], [1, 3], [2, 4], [3], [6, 8], [5, 7], [6], [5], [1, 10], [9]]
var visited: [Bool] = [Bool](repeating: false, count: graph.count)

func dfs (_ node: Int) {
    //현재 노드를 방문 처리
    visited[node] = true
    
    print(node)
    
    //현재 노드와 연결된 다른 노드를 재귀적으로 방문
    for i in graph[node] {
        if !visited[i] {
            dfs(i)
        }
    }
}

dfs(1) //1 2 3 4 5 6 7 8 9 10

• swift 스택 구현

struct InStack { 
    var items: [Int] = []

    mutating func push(_ item: Int) { 
        items.append(item) 
    } 
    mutating func pop() { 
        items.removeLast() 
    } 
}

var integerStack: InStack = InStack() 
integerStack.push(5) 
integerStack.push(10) 
print(integerStack.items) 
integerStack.pop() 
print(integerStack.items)

//[5, 10] 
//[5]

---

2. BFS (너비 우선 탐색 - Breadth-First Search)

• 최대한 넓게 이동한 다음, 더 이상 갈 수 없을 때 아래로 이동
• 주로 두 노드 사이의 최단 경로를 찾고 싶을 때 이 방법을 선택합니다.
• 큐를 이용해서 구현 (queue를 활용하기 때문에 FIFO)
  

---

3. 그리디

//거스름돈 갯수 
func solution(_ change: Int) -> Int { 
  var changes: Int = change 
  let coins: [Int] = [500, 100, 50, 10] 
  var count: Int = 0  
  // O(n*n) 
  // for i in coins { 
  //   while changes != 0 && changes >= i { 
  //     changes = changes - i 
  //     count += 1 
  //   } 
  // } 
  // O(n) 
  for coin in coins { 
    count += changes / coin //몫 
    changes %= coin //나머지 
    print(count, changes) 
  } 
  return count 
} 
print(solution(1260))

2 260 
4 60 
5 10 
6 0 
6

---

4. 순열 / 조합

//재귀 조합
func solution(_ number:[Int]) -> Int { 
    var answer: Int = 0 
    func recursive(_ index: Int, _ now: [Int]) { 
        if now.count == 3 { 
            if now.reduce(0, +) == 0 { answer += 1 } 
   
            return 
        } 
         
        for i in index..<number.count { 
            recursive(i + 1, now + [number[i]]) 
        } 
    } 
     
    recursive(0, []) 
   
    return answer 
}

solution([-2, 3, 0, 2, -5]) //	2 
//solution([-3, -2, -1, 0, 1, 2, 3]) //	5

---

5. 정렬

//선택정렬 (O(N2))
func solution(_ orig_array: [Int]) -> [Int] { 
    var min_index: Int = 0 
    var array: [Int] = orig_array 
     
    for i in 0..<array.count { 
        min_index = i //0,1,2,3,4,5,6,7,8,9
        for j in (i + 1)..<array.count { //1,2,3,4,5,6,7,8,9
            if array[min_index] > array[j] { 
                min_index = j 
            } 
        } 
        array.swapAt(i, min_index) 
    } 
    print(array) 
    return array 
}
solution([7, 5, 9, 0, 3, 1, 6, 2, 4, 8]) //[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

//삽입정렬 (O(N2))
func solution(_ orig_array: [Int]) -> [Int] { 
    var array: [Int] = orig_array 
     
    for i in 1..<array.count { //1,2,3,4,5,6,7,8,9 
        for j in (1...i).reversed() { //
            //print(i, j) 
            if array[j] < array[j - 1] { 
                array.swapAt(j, j - 1)  
            } else { 
                break 
            } 
        } 
    } 
    print(array) 
    return array 
} 
solution([7, 5, 9, 0, 3, 1, 6, 2, 4, 8]) //[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

//퀵정렬 O(NlogN)
func solution(_ array: [Int]) -> [Int] { 
    if array.count < 2 { return array } 
    let pivot = array[0] 
    let left: [Int] = array.filter { $0 < pivot } 
    let right: [Int] = array.filter { $0 > pivot } 

    return solution(left) + [pivot] + solution(right) 
} 
print(solution([7, 5, 9, 0, 3, 1, 6, 2, 4, 8])) //[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

//계수정렬
//O(n + K) n데이터 갯수, k최댓값(최댓값이 작고 동일한 값이 여러개 존재할 때) 
func solution(_ array: [Int]) -> [Int] {  
    //값 종류만큼 배열 생성(값을 안덱스로 봄) 
    var count: [Int] = [Int](repeating: 0, count: 10) 
    var answer: [Int] = [] 
    for i in 0..<array.count { 
        count[array[i]] += 1 
    } 
    //[1, 2, 1, 2, 1, 1, 1, 3, 1, 1] 
    for i in 0..<count.count { 
        for j in 0..<count[i] { 
            answer.append(i) 
        } 
    } 
     
    return answer 
}  
print(solution([3, 7, 5, 7, 1, 9, 0, 3, 1, 7, 6, 2, 4, 8])) //[0, 1, 1, 2, 3, 3, 4, 5, 6, 7, 7, 7, 8, 9]

알고리즘	시간 복잡도	공간 복잡도	특징
선택 정렬	O(N2)	O(N)	간단
삽입 정렬	O(N2)	O(N)	거의 정렬이 되어 있을때 빠름, O(N)까지 가능
퀵 정렬	O(NlogN)	O(N)	대부분의 경우 적합, 빠름, 최악의 경우 O(N2)이 나올수 있음
계수 정렬	O(N + K)	O(N + K)	중복데이터, 최대값을 크기가 작을때 유리

• 일반적인 정렬 함수(sorted)는 최소 O(NlogN)의 시간 복잡도를 보장함

---

6. 탐색

• 순차탐색
  • 정렬되지 않은 리스트에서 데이터를 찾음
  • O(N)
• 이진탐색
  • O(logN)
  • 원소의 갯수가 반으로 줄어드는 점에서 퀵정렬과 유사

//재귀함수
func solution(_ array: [Int], _ target:Int, _ start: Int, _ end: Int) -> Int {
    if start > end {
        print(-1)
        return -1
    }
    //중간점
    var mid: Int = (start + end) / 2
    //중간점과 찾을 수가 같다면 해당 숫자의 위치 반환
    if array[mid] == target {
        print(mid + 1)
        return mid + 1
    //중간점의 값보다 찾을 수가 적을 경우 왼쪽 영역 확인
    } else if array[mid] > target {
        solution(array, target, start, mid - 1)
    } else {
    //중간점의 값보다 찾을 수가 적을 경우 오른쪽 영역 확인    
        solution(array, target, mid + 1, end)
    }
    return 0
}
solution([1,3,5,7,9,11,13,15,17,19], 7, 0, 9) //찾을 수 7, 답 4

//반복문
func solution(_ array: [Int], _ target: Int, _ start: Int, _ end: Int) -> Int {
    var starts: Int = start
    var ends: Int = end
    while starts <= ends {
        var mid: Int = (starts + ends) / 2
        if array[mid] == target {
            print(mid + 1)
            return mid + 1
        } else if array[mid] > target {
            ends = mid - 1
        } else {
            starts = mid + 1
        }
    }
    return -1
}
solution([1,3,5,8,10,34,56,89,93,100, 102], 8, 0, 9) //찾을 수 8, 답 4

---

7. 동적 프로그래밍

• 하향식(Top-Down)
  • Memoization(Caching)
  • 재귀함수를 사용하여 작은 부분의 결과값으로 큰 부분의 결과를 도출

var dp: [UInt] = [UInt](repeating: 0, count: 100)
func fibo(_ x: Int) -> UInt {
    if x == 1 || x == 2 {
        return UInt(1)
    }
    if dp[x] != 0 {
        return UInt(dp[x])
    } else {
        dp[x] = fibo(x - 1) + fibo(x - 2)
        return UInt(dp[x])
    }
}
print(fibo(93))

• 상향식(Bottom-Up)
  • 반복문 사용

var dp: [UInt] = [UInt](repeating: 0, count: 90)
func fibo(_ x: Int) -> UInt {
    dp[1] = 1
    dp[2] = 1
    for i in 3..<dp.count {
        dp[i] = UInt(dp[i - 1]) + UInt(dp[i - 2])
    }
    return UInt(dp[x])
}
print(fibo(89))