개요

공부한 시간에 따른 성적의 변화를 선형회귀로 학습한다.
개념을 익히기 위해 머신러닝 라이브러리는 여기서는 사용하지 않는다.

선형회귀?

머신러닝에서 예측선을 긋는 것을 선형 회귀라는 통계학 용어로 설명한다.

아래에서 학습 시간과 성적의 관계 데이터를 가지고 설명한다.

Data - 학습시간과 성적의 관계

내용	-	-	-	-
공부한 시간	2	4	6	8
성적	81	93	91	97

독립변수와 종속변수

위의 표처럼 '공부한 시간(학습시간)'이라는 변수를 $x$로 하고 '독립변수'라고 부르며, 이 독립변수에 따라 달라질 수 있는 $y$값(성적)을 '종속변수'라고 부르기로 한다.

선형회귀에서는 독립변수 $x$를 사용해 종속변수 $y$의 움직임을 예측하고 설명한다.

단순 선형 회귀와 다중 선형 회귀

선형회귀 중, 하나의 $x$값으로 y값을 설명할 수 있을 때 이를 단순 선형 회귀(simple linear regression)이라고 하며, $x$값이 여러개 필요할 때에는 다중 선형 회귀(multiple linear regression)이라고 한다.

단순 선형 회귀

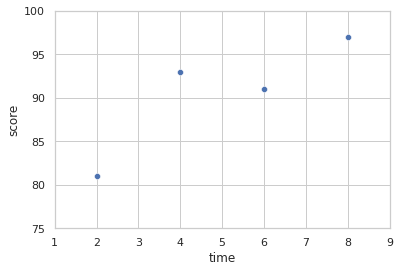
위의 표에서의 공부한 시간과 성적의 관계를 그래프로 나타내면 위와 같다.

각 점들의 위치가 $x$가 커질수록(공부 시간이 길어질수록) $y$가 커지는(점수가 오른쪽 위 방향으로 올라가는) 선형적인 관계에 있으며, 여기에서의 선은 직선이다.
그러므로 일차함수 그래프라고 할 수 있으며 이것은 $𝗒=ax+b$라고 할 수 있다.
위에서 설명한대로 $x$는 독립변수이며 $y$는 종속변수이다.

$x$와 $y$는 변화하므로 $a$($x$의 기울기)와 $b$($y$절편)를 구해야 값을 정확하게 계산할 수 있다.
이것이 선형회귀의 목적이라고 할 수 있다.

최소제곱법

(1) 기울기 $a$를 구하는 방법

𝛼 = $\frac {(x - x평균)(y - y평균)의 합}{(x - x평균)^2}$

즉, $x$의 편차(각 $x$값과 평균과의 차이)를 제곱한 값들을 더해서 분모에, $x$의 편차와 $y$의 편차를 곱한 값들을 더한 값을 분자에 놓으면 기울기가 나온다.

위의 표에서,
공부한 시간($x$)의 평균

(2 + 4+ 6 + 8) / 4 = 5

성적($y$)의 평균

(81 + 93 + 91 + 97) / 4 = 90.5

이 되며, 위에서 제시한 기울기 𝛼를 구하는 식에 대입한다면,

𝛼 = $\frac {(2 - 5)(81 - 90.5) + (4 - 5)(93 - 90.5)+(6 - 5)(91 - 90.5) + (8 - 5)(97 - 90.5)}{(2 - 5)^2 + (4 - 5)^2 + (6 - 5)^2 + (8 - 5)^2}$
= $\frac {46}{20}$ = 2.3```

기울기 $a$가 2.3이라는 걸 알 수 있다.

(2) $y$절편 $b$ 구하기

$b$ = $y$평균 - ($x$의 평균×기울기 $a$)

위에서 𝗒평균, 𝒙의 평균, 기울기 𝛼 모두를 알 수 있으므로 대입 해 보면,

$b$ = 90.5 - (5×2.3) = 79

즉, 위 성적 그래프의 일차함수는

$y$ = 2.3$x$ + 79

라는 결과가 나온다.

이 함수를 이용해 우리가 원래의 학습시간에 따라 얻었어야 할 점수를 예측하자면 아래와 같다.

내용	-	-	-	-
공부한 시간	2	4	6	8
성적	81	93	91	97
예측값	83.6	88.2	92.8	97.4

공부한 시간에 따른 실제 성적과 일차함수 대입을 통한 예측값의 그래프는 아래와 같다.
score(파란색 점)가 실제 점수, predict(주황색 점)가 일차함수를 통한 예측값을 나타낸다.

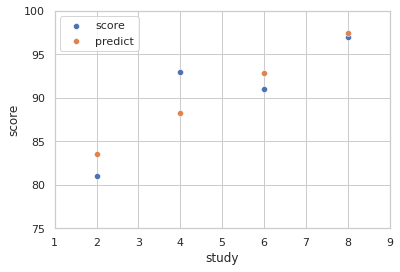
predict의 점 사이를 그어본다면, 아래의 그래프처럼 직선이 됩니다.

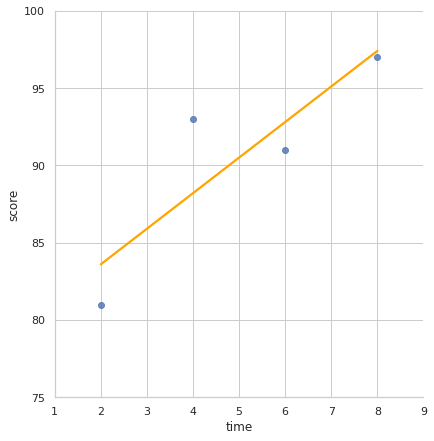
Python코딩으로 구해보는 최소제곱

지금까지 언급된 것들을 numpy를 이용해 구해보는 Python 코드는 아래와 같다.

코드

import numpy as np
x = [2, 4, 6, 8] # 공부한 시간
y = [81, 93, 91, 97] # 실제 시험 점수

# x평균과 y평균
mx = np.mean(x)
my = np.mean(y)

print("x의 평균값: ", mx)
print("y의 평균값: ", my)

# 기울기 공식의 분모
divisor = sum([(i - mx)**2 for i in x]) # x편차의 제곱을 모두 더한다.

# 기울기 공식의 분자
def top(x, mx, y, my):
  d = 0
  # x의 편차와 y의 편차를 sum 한다.
  for i in range(len(x)):
    d += (x[i] - mx) * (y[i] - my)
  return d

dividend = top(x, mx, y, my)

print("분모: ", divisor)
print("분자: ", dividend)

# 기울기
a = dividend / divisor
# y절편
b = my - (mx * a)

# 출력
print("기울기 a =", a)
print("y절편 b =", b)

출력

x의 평균값: 5.0
y의 평균값: 90.5
분모: 20.0
분자: 46.0
기울기 a = 2.3
y절편 b = 79.0

---

평균제곱오차

위의 문제에서는 일차함수로 해결이 가능했으나 실제 머신러닝,딥러닝에서는 하나의 입력변수만으로는 문제 해결이 안 되는 부분이 대부분이다.
그리하여 일단 임의의 선을 그린 뒤에 얼마나 잘 그려졌는지를 평가하여 수정해 나가는 방법을 사용해야 한다. 이 때 이 선의 오차를 평가하는 알고리즘 중 평균 제곱 오차(mean square error, MSE)가 가장 많이 사용된다.

오차

오차 = 예측값($\hat{y}$) - 실제값($y$)

보통 선형 그래프에서 기울기가 잘못될 경우, 실제 값과의 오차가 점점 크게 벌어지게 된다.
이 오차들은 + 또는 -의 값을 가지는데 단순히 sum 해 버리면 0가 될 수 있는 여지가 있다.
그래서 각 오차들은 제곱한 후에 더해줘야 한다.

오차의 합 = $\displaystyle\sum_{i}^{n}$($y_i-\hat{y_i})^2$

$y_i$는 $x_i$에 대응하는 '실제의 값'이며, $\hat{y_i}$는 $x_i$를 함수에 대입함으로써 생성되는 '예측값'이다.

위에서 구한 오차의 합을 $n$으로 나누면 오차 합의 평균을 구할 수 있으며 이것을 평균 제곱 오차(Mean Squared Error, MSE)라고 한다.

선형회귀란 임의의 직선을 그어 이에 대한 평균 제곱 오차(MSE)를 구하고, 이 값을 가장 작게 만들어 주는 $a$와 $b$값을 찾아가는 작업이다.

Python 코딩으로 구해보는 평균제곱오차

코드

import numpy as np

fake_a_b = [3, 76] # 임의로 정한 기울기 a와 절편 b값

data = [[2, 81], [4, 93], [6, 91], [8, 97]]

x = [i[0] for i in data] # 시간 리스트
y = [i[1] for i in data] # 점수 리스트

def predict(x):
  """y=ax+b에 a와 b값을 대입하여 결과를 출력하는 함수"""
  return fake_a_b[0]*x + fake_a_b[1]

def mse(y, y_hat):
  """MSE함수"""
  return ((y - y_hat) ** 2).mean() # y와 y예측값 편차의 제곱의 평균을 낸다.

def mse_val(y, predict_result):
  """MSE함수를 각 y값에 대입하여 최종 값을 구하는 함수"""
  return mse(np.array(y), np.array(predict_result))

# 예측 값이 들어갈 빈 리스트
predict_result = []

# 모든 x값을 한 번씩 대입
for i in range(len(x)):
  # predict_result 리스트 완성
  predict_result.append(predict(x[i]))
  print("공부한 시간 = %.f, 실제 점수 = %.f, 예측 점수=%.f" % (x[i], y[i], predict(x[i])))

# 최종 MSE 출력
print("mse 최종값: " + str(mse_val(y, predict_result)))

출력값

공부한 시간 = 2, 실제 점수 = 81, 예측 점수=82
공부한 시간 = 4, 실제 점수 = 93, 예측 점수=88
공부한 시간 = 6, 실제 점수 = 91, 예측 점수=94
공부한 시간 = 8, 실제 점수 = 97, 예측 점수=100
mse 최종값: 11.0

---

경사하강법

평균제곱오차를 구하는 과정에서, $a$값을 너무 크게 잡으면 오차가 커진다는 점을 알았다. 그런데, 너무 작게 잡아도 역시 오차가 커지게 된다.즉, 기울기 $a$와 오차 사이에는 상관 관계가 있다고 할 수 있다.
이럴 때는 경사하강법을 이용해야 한다.

개요

기울기가 0인, 즉, 미분 값이 0인 지점을 찾는다.

과정

(1)그래프 상의 어느 지점(선 위) $a_1$에서 미분을 구한다.
(2)구해진 기울기의 반대방향으로 적당히 이동한 다음 이동시킨 $a_2$의 미분을 구한다.
(3)(2)에서 구한 미분 값이 0이 아니면 위 과정 반복.
(그래프 그리는 방법을 몰라서 생략한다. 죄송...)

학습률

기울기 부호를 바꿔 이동을 시키려면 적절한 거리를 찾아야 하는데 너무 멀리 이동시키면 $a$가 한 점으로 모이지 않고 오히려 기울기 0 지점으로부터 더 멀어져 버린다.
그래서 얼마만큼 이동시킬지를 신중하게 정해야 하며 이것을 학습률이라고 한다.
즉, 경사하강법은 오차의 변화에 따라 이차 함수 그래프를 만들고 적절한 학습률을 설정해 미분값이 0인 지점을 구하는 것이다.
$y$절편 $b$의 값도 이와 같은 성질을 가진다. $b$값이 너무 크면 오차도 함께 커지며, 너무 작아도 오차가 커진다. 그래서 $b$값을 구할 때에도 경사 하강법을 사용한다.

평균 제곱 오차 편미분

$\frac{1}{n}\displaystyle\sum_{i}^{n}$($y_i-\hat{y_i})^2$

여기에서 $\hat{y_i}$은 $x_i$를 집어넣었을 때의 값이므로 $y_i=ax_i+b$를 대입하면

$\frac{1}{n}\displaystyle\sum_{i}^{n}$($y_i-(ax_i+b))^2$

여기에서 주의할 점은, 궁금한 값은 $a$와 $b$이므로 이 필요한 값들로만 미분해야 한다.
$a$로 편미분 한 결과

$\frac{2}{n}\sum$($ax_i+b-y_i)x_i$

$b$로 편미분 한 결과

$\frac{2}{n}\sum$($ax_i+b-y_i)$

코드

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 공부 시간 X와 성적 Y의 리스트 만들기
data = [[2, 81], [4, 93], [6, 91], [8, 97]]
x = [i[0] for i in data]
y = [i[1] for i in data]

# 그래프로 나타내기
plt.figure(figsize=(8, 5))
plt.scatter(x, y)
plt.show()

# 리스트로 되어 있는 x와 y값을 넘파이 배열로 변환(인덱스를 주어 하나씩 불러와 계산이 가능하게 하기 위함)
x_data = np.array(x)
y_data = np.array(y)

# 기울기 a와 절편 b의 값 초기화
a = 0
b = 0

# 학습률 정하기
lr = 0.03

# 몇 번 반복할지 설정
epochs = 2001

# 경사 하강법 시작
for i in range(epochs): # epoch 수만큼 반복
  y_pred = a * x_data + b # y를 구하는 식
  error = y_data - y_pred # 오차를 구하는 식

  # 평균 제곱 오차를 a로 미분한 결과
  a_diff = -(2 / len(x_data)) * sum(x_data * (error))
  # 평균 제곱 오차를 b로 미분한 결과
  b_diff = -(2 / len(x_data)) * sum(error)

  a = a - lr * a_diff # 미분 결과에 학습률을 곱한 후 기존의 a값을 업데이트
  b = b - lr * b_diff # 미분 결과에 학습률을 곱한 후 기존의 b값을 업데이트

  if i % 100 == 0: # 100번씩 반복될 때마다 현재의 a값, b값 출력
    print("epoch=%d, 기울기=%.04f, 절편=%.04f" % (i, a, b))

# 앞서 구한 기울기와 절편을 이용해 그래프 다시 그리기
y_pred = a * x_data + b
plt.scatter(x, y)
plt.plot([min(x_data), max(x_data)], [min(y_pred), max(y_pred)])
plt.show()

출력

epoch=0, 기울기=27.8400, 절편=5.4300
epoch=100, 기울기=7.0739, 절편=50.5117
epoch=200, 기울기=4.0960, 절편=68.2822
epoch=300, 기울기=2.9757, 절편=74.9678
epoch=400, 기울기=2.5542, 절편=77.4830
epoch=500, 기울기=2.3956, 절편=78.4293
epoch=600, 기울기=2.3360, 절편=78.7853
epoch=700, 기울기=2.3135, 절편=78.9192
epoch=800, 기울기=2.3051, 절편=78.9696
epoch=900, 기울기=2.3019, 절편=78.9886
epoch=1000, 기울기=2.3007, 절편=78.9957
epoch=1100, 기울기=2.3003, 절편=78.9984
epoch=1200, 기울기=2.3001, 절편=78.9994
epoch=1300, 기울기=2.3000, 절편=78.9998
epoch=1400, 기울기=2.3000, 절편=78.9999
epoch=1500, 기울기=2.3000, 절편=79.0000
epoch=1600, 기울기=2.3000, 절편=79.0000
epoch=1700, 기울기=2.3000, 절편=79.0000
epoch=1800, 기울기=2.3000, 절편=79.0000
epoch=1900, 기울기=2.3000, 절편=79.0000
epoch=2000, 기울기=2.3000, 절편=79.0000

기울기$a$와 절편$b$의 값이 처음에 최소제곱법으로 구한 2.3과 79에 수렴해 가는 것을 볼 수 있다.

다중 선형 회귀

위에서는 6시간 공부한 결과가 4시간 공부한 결과에 비해 좋지 않는 등의 오차가 생겼다.
이것은 학습시간 외의 다른 결과 또한 시험 결과에 영향을 끼쳤기 때문이라고 할 수 있다.
더 정확한 예측을 위해 추가적인 정보가 필요하다.

변수 추가

공부한 시간($x_1$)	2	4	6	8
과외 수업 횟수($x_2$)	0	4	2	3
성적($y$)	81	93	91	97

기존의 하나만 있던 $x$를 $x_1$로 생각하기로 하고, 과외 수업 횟수 정보를 새로 부여하여 이것을 $x_2$라고 한다.
그러면 성적 $y$를 구하는 식은 아래와 같이 바뀐다.

$y=a_1x_1+a_2x_2+b$

또한 여기서도 $a_1$과 $a_2$를 구하기 위해서 경사하강법을 그대로 적용한다.

코드

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d

#공부시간 X와 성적 Y의 리스트를 만듭니다.
data = [[2, 0, 81], [4, 4, 93], [6, 2, 91], [8, 3, 97]]
x1 = [i[0] for i in data]
x2 = [i[1] for i in data]
y = [i[2] for i in data]

#그래프로 확인해 봅니다.
ax = plt.axes(projection='3d')
ax.set_xlabel('study_hours')
ax.set_ylabel('private_class')
ax.set_zlabel('Score')
ax.dist = 11 
ax.scatter(x1, x2, y)
plt.show()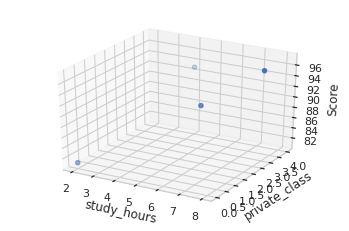

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d

#공부시간 X와 성적 Y의 리스트를 만듭니다.
data = [[2, 0, 81], [4, 4, 93], [6, 2, 91], [8, 3, 97]]
x1 = [i[0] for i in data]
x2 = [i[1] for i in data]
y = [i[2] for i in data]

#그래프로 확인해 봅니다.
ax = plt.axes(projection='3d')
ax.set_xlabel('study_hours')
ax.set_ylabel('private_class')
ax.set_zlabel('Score')
ax.dist = 11 
ax.scatter(x1, x2, y)
plt.show()

#리스트로 되어 있는 x와 y값을 넘파이 배열로 바꾸어 줍니다.(인덱스를 주어 하나씩 불러와 계산이 가능해 지도록 하기 위함입니다.)
x1_data = np.array(x1)
x2_data = np.array(x2)
y_data = np.array(y)

# 기울기 a와 절편 b의 값을 초기화 합니다.
a1 = 0
a2 = 0
b = 0

#학습률을 정합니다.
lr = 0.05 

#몇 번 반복될지를 설정합니다.(0부터 세므로 원하는 반복 횟수에 +1을 해 주어야 합니다.)
epochs = 2001 

#경사 하강법을 시작합니다.
for i in range(epochs): # epoch 수 만큼 반복
    y_pred = a1 * x1_data + a2 * x2_data + b  #y를 구하는 식을 세웁니다
    error = y_data - y_pred  #오차를 구하는 식입니다.
    a1_diff = -(1/len(x1_data)) * sum(x1_data * (error)) # 오차함수를 a1로 미분한 값입니다. 
    a2_diff = -(1/len(x2_data)) * sum(x2_data * (error)) # 오차함수를 a2로 미분한 값입니다. 
    b_new = -(1/len(x1_data)) * sum(y_data - y_pred)  # 오차함수를 b로 미분한 값입니다. 
    a1 = a1 - lr * a1_diff  # 학습률을 곱해 기존의 a1값을 업데이트합니다.
    a2 = a2 - lr * a2_diff  # 학습률을 곱해 기존의 a2값을 업데이트합니다.
    b = b - lr * b_new  # 학습률을 곱해 기존의 b값을 업데이트합니다.
    if i % 100 == 0:    # 100번 반복될 때마다 현재의 a1, a2, b값을 출력합니다.
        print("epoch=%.f, 기울기1=%.04f, 기울기2=%.04f, 절편=%.04f" % (i, a1, a2, b))

epoch=0, 기울기1=23.2000, 기울기2=10.5625, 절편=4.5250
epoch=100, 기울기1=6.4348, 기울기2=3.9893, 절편=43.9757
epoch=200, 기울기1=3.7255, 기울기2=3.0541, 절편=62.5766
epoch=300, 기울기1=2.5037, 기울기2=2.6323, 절편=70.9656
epoch=400, 기울기1=1.9527, 기울기2=2.4420, 절편=74.7491
epoch=500, 기울기1=1.7042, 기울기2=2.3562, 절편=76.4554
epoch=600, 기울기1=1.5921, 기울기2=2.3175, 절편=77.2250
epoch=700, 기울기1=1.5415, 기울기2=2.3001, 절편=77.5720
epoch=800, 기울기1=1.5187, 기울기2=2.2922, 절편=77.7286
epoch=900, 기울기1=1.5084, 기울기2=2.2886, 절편=77.7992
epoch=1000, 기울기1=1.5038, 기울기2=2.2870, 절편=77.8310
epoch=1100, 기울기1=1.5017, 기울기2=2.2863, 절편=77.8453
epoch=1200, 기울기1=1.5008, 기울기2=2.2860, 절편=77.8518
epoch=1300, 기울기1=1.5003, 기울기2=2.2858, 절편=77.8547
epoch=1400, 기울기1=1.5002, 기울기2=2.2858, 절편=77.8561
epoch=1500, 기울기1=1.5001, 기울기2=2.2857, 절편=77.8567
epoch=1600, 기울기1=1.5000, 기울기2=2.2857, 절편=77.8569
epoch=1700, 기울기1=1.5000, 기울기2=2.2857, 절편=77.8570
epoch=1800, 기울기1=1.5000, 기울기2=2.2857, 절편=77.8571
epoch=1900, 기울기1=1.5000, 기울기2=2.2857, 절편=77.8571
epoch=2000, 기울기1=1.5000, 기울기2=2.2857, 절편=77.8571