Background

ML based Recsys

https://velog.io/@kms39273/Collaborative-Filtering

Problem state

Matrix Factorization(MF)은 user와 item의 상호작용을 학습하는 한 방법으로, user-item 공간의 latent feature들의 inner product를 통해 두 관계를 표현하게 된다. 그러나 Matrix Factorization은 기본적으로 선형적인 모델이므로, 비선형적인 사용자-아이템 상호작용을 표현하기에 한계가 있음을 지적한다.

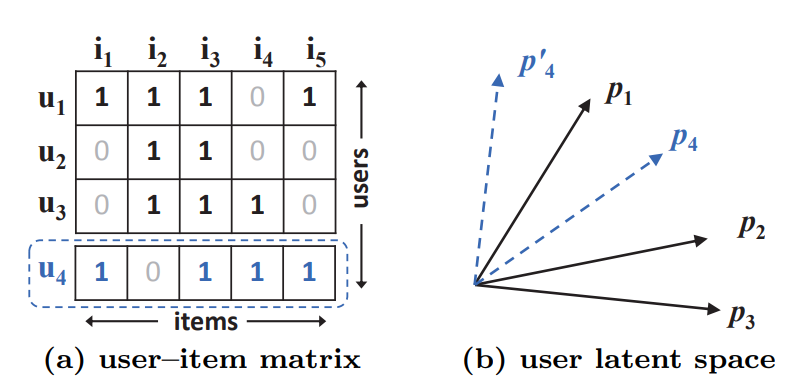
u4는 u1, u3, p2순서로 가깝지만, 선형적으로는 벡터화하면 이를 표현할 수 없다.
해결 방법
많은 latent factors K를 사용하는 것
-> 하지만 sparse할 경우 데이터 과적합이 발생할 수 있음
논문에서는 non-linear한 DNN을 활용함으로서 한계 해결했다.

Methodology

A Neural Collaborative Filtering(NCF)
A NCF instance that generalizes the MF model(GMF)
A NCF instance that models non-linearities with a multi-layer perceptron(MLP)
A NCF instance NewMF that fuses GMF and MLP.

Learning From Implicit Data

논문은 user의 행동을 통해 선호도를 간접적으로 반영하는 Implicit Feedback 활용
장점 : rating이나 review 같은 Explicit Feedback과 비교했을 때 Implicit Feedback은 자동으로 수집될 수 있음
단점 : user 만족도가 관찰되지 않고 부정적 feedback이 부족하기 때문에 활용하기 어려움

Recommendation Problem With Implicit Feedback

을 사용하는 추천 문제는 관찰되지 않은 등급을 예측하는 문제입니다. 모델 기반 접근법은 데이터가 기본 모델에 의해 생성되거나 설명될 수 있다고 가정합니다.

Negative Data Handling

Negative Data의 부재 처리 방법
관찰되지 않은 항목들을 negative feedback으로 처리
관찰되지 않은 항목들에서 negative instance 샘플링

Neural Collaborative Filtering(NCF)

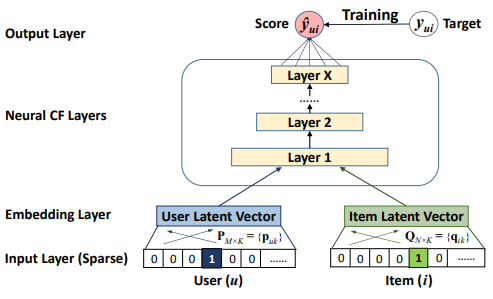
inner product가 아닌 dnn을 통과하게 된다.
Input Layer에서는 관찰된 사용자와 아이템만이 입력 특성으로 사용되며, 이들은 one-hot 인코딩을 통해 binary sparse vector로 변환된다.
또한, 콘텐츠 특성을 사용하여 사용자와 아이템을 표현함으로써 cold start문제(충분히 정보가 적재되지 않아 추천을 할 수 없는 문제)를 해결할 수 있도록 모델을 조정할 수 있다.
Embedding Layer는 sparse representation을 dense vector로 변환하는 Fully Connected 레이어이다. 얻어진 user(item) embedding은 각각 사용자와 아이템의 latent vector로 볼 수 있다.
Neural CF Layer는 user(item) embedding을 사용하여 latent vector를 predict score로 매핑한다. 각 레이어는 ser-item interaction의 특정 latent 구조를 발견하는 데 사용될 수 있다. 마지막 레이어 X는 모델의 용량을 결정한다.
Output Layer는 예측 등급 $y_{ui}^{\hat{}}$를 나타낸다. 학습은 $y_{ui}^{\hat{}}$와 타겟 $y_{ui}$ 사이의 pointwise loss를 최소화하는 방식으로 수행됩니다. 또한, pairwise learning도 가능하다.

Pointwise learning: 이 방법은 예측값 $y_{ui}^{\hat{}}$와 타겟값 $y_{ui}$ 사이의 제곱 손실(square loss)을 최소화하는 것을 목표로 한다. 이는 각각의 사용자-아이템 쌍에 대해 개별적으로 모델의 예측과 실제 값 사이의 차이를 최소화하려는 접근법이다.

Pairwise learning: 이 방법은 관찰된 아이템이 관찰되지 않은 아이템보다 더 높은 순위를 가져야 한다는 원칙에 기반을 두고 있다. 이는 모델이 관찰된 아이템의 예측 점수 $y_{ui}^{\hat{}}$와 관찰되지 않은 아이템의 예측 점수 사이의 마진을 최대화하려는 접근법이다. 이 방법은 모델이 사용자의 선호도에 따라 아이템을 순위를 매기는 능력을 향상시키는 데 도움이 된다.

Generalized Matrix Factorization (GMF)

이 모델은 Matrix Factorization (MF)를 특별한 경우로 해석하는 방법을 보여준다.

$φ_1(p_u, q_i) = p_u \odot q_i$

• $\phi_1(p_u, q_i)$: 이는 GMF 모델에서 첫 번째 레이어의 매핑 함수를 나타냅니다. 이 함수는 사용자와 아이템의 잠재 벡터를 입력으로 받아 그들 간의 상호작용을 계산한다.
• $p_u$와 $q_i$: 이는 각각 사용자 u와 아이템 i의 latent vector를 나타낸다. 이 벡터들은 사용자와 아이템의 특성을 나타내며, 임베딩 레이어를 통해 학습된다.
• $\odot$: 이 기호는 벡터의 element-wise product을 나타낸다. 이 연산은 사용자와 아이템의 잠재 벡터 간의 상호작용을 모델링한다.

그런 다음 이 벡터를 출력 레이어로 투영한다.

$y_{ui}^{\hat{}} = a_{out}(h^T(p_u \odot q_i))$

• $y_{ui}^{\hat{}}$는 사용자 u와 아이템 i 간의 예측된 상호작용을 나타낸다. 이는 모델이 예측한 사용자 u의 아이템 i에 대한 평점 또는 선호도를 의미할 수 있다.
• $a_{out}$는 출력 레이어의 활성화 함수이다.
• $h$는 출력 레이어의 가중치이다.

만약 우리가 출력 레이어의 활성화 함수를 항등 함수로 설정하고, 모든 가중치를 1로 설정하면, MF 모델과 동일하게 작동한다. GMF는 MF를 쉽게 일반화하고 확장할 수 있도록 해준다.
활성화함수는 sigmoid function 사용
손실함수는 logloss를 활용해서 h를 학습시켰다.

Multi-Layer Perceptron (MLP)

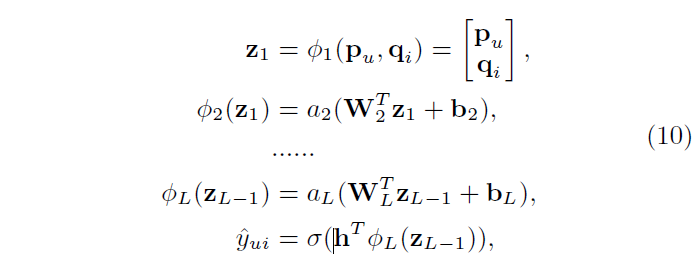
일반적인 MLP를 제안한다.

Fusion of GMF and MLP

• GMF는 linear kernel을 이용해 latent feature interaction을 모델링한다.
• 반면 MLP는 non-linear kernel을 이용해 데이터에서 interaction function 학습한다.
  따라서 두 모델을 결합하면 사용자-아이템 상호작용을 더 잘 모델링할 수 있을 것이라는 가정을 하였고, 이를 위해 두 가지 방법이 제안되었다.

Straightforward solution: GMF와 MLP가 동일한 Embedding layer를 통해 생성된 동일한 latent feature vector를 공유하도록 한다. 하지만 이 방법은 두 모델이 최적의 잠재 특징 벡터 크기가 다를 경우, 성능이 좋지 않을 수 있다는 한계가 있다.

$\hat{y}_{ui} = \sigma(h^T(a(p_u \odot q_i + W[p_u, q_i] + b))$

• $\hat{y}_{ui}$: 사용자 u와 아이템 i 사이의 예측 상호작용 점수, 사용자가 아이템에 얼마나 관심을 가질 것인지를 나타낸다.
• $\sigma(\cdot)$: 시그모이드 함수
• $h^T$: 학습 가능한 가중치 벡터의 전치이다. GMF와 MLP의 출력을 결합하여 최종 예측 값을 생성하는데 사용된다.
• $a(\cdot)$: 활성화 함수
• $p_u$ and $q_i$: 각각 사용자 u와 아이템 i의 임베딩 벡터
• $W[p_u, q_i]$: 사용자 벡터와 아이템 벡터를 결합한 후, 이를 가중치 행렬 $W$에 곱하는 연산
• $b$: 편향 벡터

Paper solution: GMF와 MLP가 각각 별도의 잠재 특징 벡터를 학습한다. 그리고 이 두 벡터를 마지막 hidden layer에서 연결하여 모델을 결합한다. 이를 Neural Matrix Factorization (NeuMF) 레이어라고 한다.

$\phi_{GMF} = p_{G_u} \odot q_{G_i}$**

• $p_{G_u}$: 사용자 u에 대한 GMF 임베딩 벡터
• $q_{G_i}$: 아이템 i에 대한 GMF 임베딩 벡터

$\phi_{MLP} = a_L(W^T_L(a_{L-1}(...a_2(W^T_2[p_{M_u}, q_{M_i}] + b_2)...)) + b_L)$**

• $W^T_L, b_L$: 각각 L번째 계층의 가중치 행렬의 전치와 편향 벡터
• $a_L$: L번째 계층의 활성화 함수

$\hat{y}_{ui} = \sigma(h^T[\phi_{GMF}, \phi_{MLP}])$

• $h^T$: 학습 가능한 가중치 벡터의 전치이며, GMF와 MLP의 출력을 결합하여 최종 예측 값을 생성하는데 사용된다.
• $\sigma(\cdot)$: 시그모이드 함수
• $\hat{y}_{ui}$: 사용자 u와 아이템 i 사이의 예측 상호작용 점수,.사용자가 아이템에 얼마나 관심을 가질 것인지를 나타낸다.

이렇게 결합된 모델은 Matrix Factorization의 선형성과 Deep Neural Network의 비선형성을 모두 활용하여 사용자-아이템 interaction 모델링한다. 이 때, $P_{uG}$와 $P_{uM}$는 각각 GMF와 MLP에 대한 사용자 임베딩을, $Q_{iG}$와 $Q_{iM}$는 각각 GMF와 MLP에 대한 아이템 임베딩을 나타낸다.

Conclusion

이 논문은 사용자-아이템 상호작용을 더욱 정확하게 모델링하기 위해 Generalized Matrix Factorization(GMF)와 Multi-Layer Perceptron(MLP)를 결합한 Neural Collaborative Filtering(NCF) 방법을 제안한다.
이 방법은 Matrix Factorization의 선형성과 Deep Neural Network의 비선형성을 모두 활용하여 복잡한 사용자-아이템 상호작용을 잘 표현할 수 있다.
논문에서는 두 가지 임베딩 방법을 제안하고, 이를 결합한 모델인 Neural Matrix Factorization(NeuMF)가 추천 시스템의 성능을 향상시킬 수 있음을 실험적으로 입증하였다.