힙(Heap)이란?
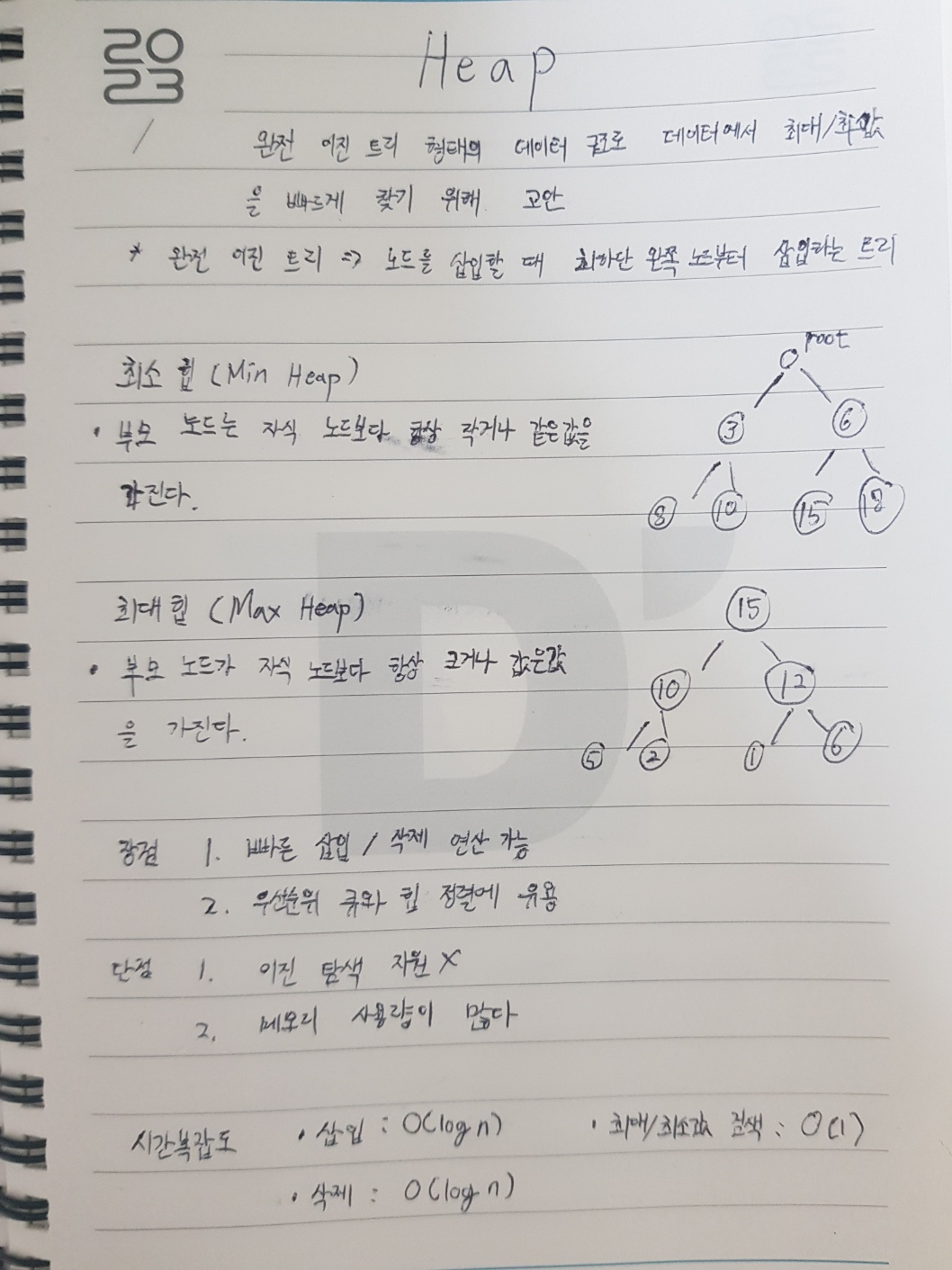
완전 이진 트리 형태의 데이터 구조로 데이터에서 최댓값과 최솟값을 빠르게 찾기 위해 고안되었다.
* 완전 이진 트리란?
=> Node를 삽입할 때 최하단 왼쪽 Node부터 차례대로 삽입하는 트리
힙(Heap) 특징
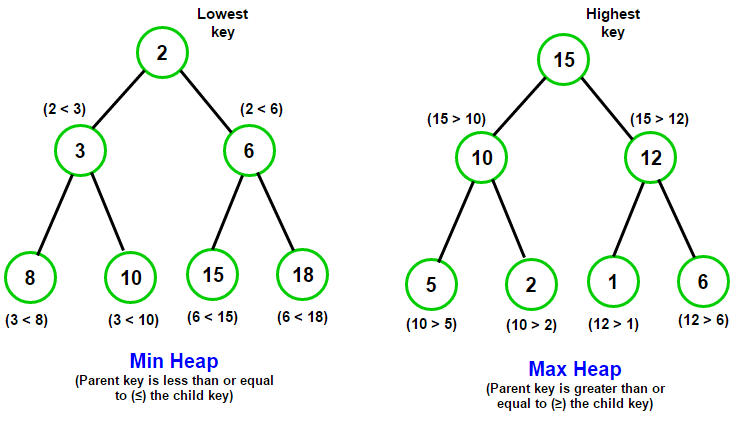
- Heap(힙)은 부모 노드와 자식 노드 간의 관계를 특별한 조건으로 정의한다. Max Heap의 경우 부모 노드는 자식 노드보다 항상 크거나 같은 값을 가지며, Min Heap의 경우 부모 노드는 자식 노드보다 항상 작거나 같은 값을 가진다.
- 빠른 삽입/삭제 연산
- Heap(힙)에서 항상 루트 노드가 최댓값 또는 최솟값을 가지며, 이를 O(1) 시간 내에 접근할 수 있다. 삽입과 삭제의 시간 복잡도는 O(log n)으로 매우 효율적이다.
- Heap(힙)은 우선순위 큐나 힙 정렬 등에서 사용되며, 이를 통해 정렬이나 최댓값/최솟값 검색 등의 작업을 효율적으로 처리할 수 있다.
힙(Heap) 동작 원리
힙(Heap)에 데이터 삽입
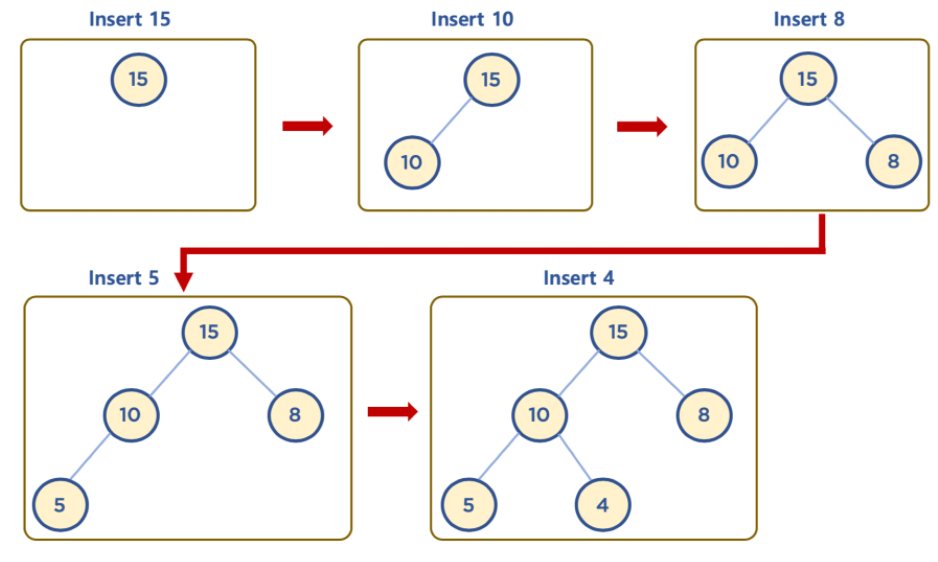
완전 이진 트리이기 때문에 삽입할 노드는 왼쪽 최하단 노드부터 채워진다.
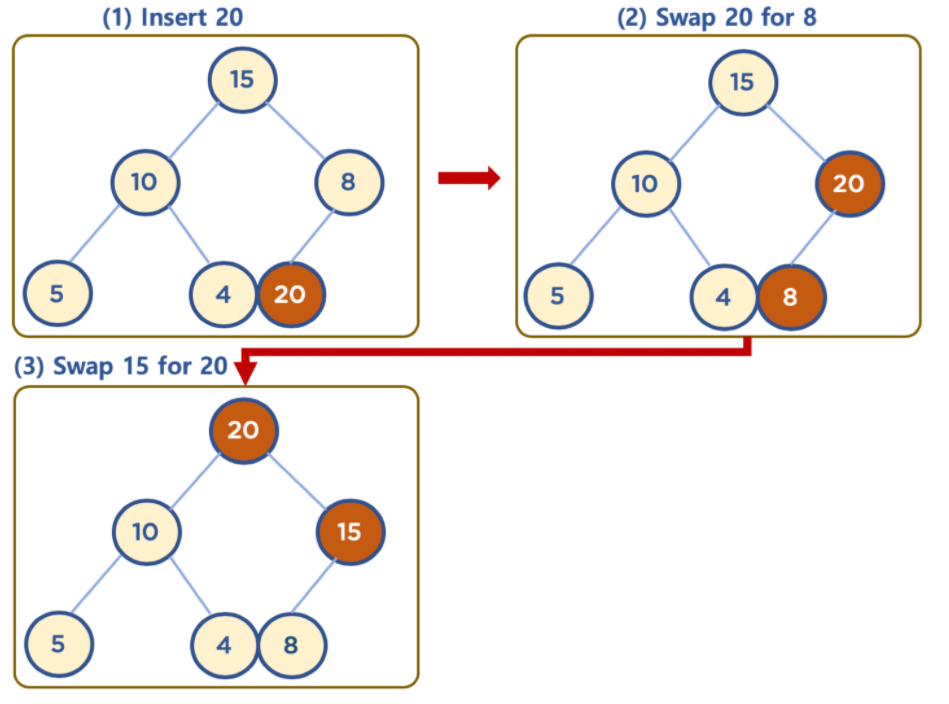
채워진 노드 위치에서 부도 노드보다 값이 클 경우 부모 노드와 위치를 바꿔주는 작업 반복
힙(Heap)의 데이터 삭제
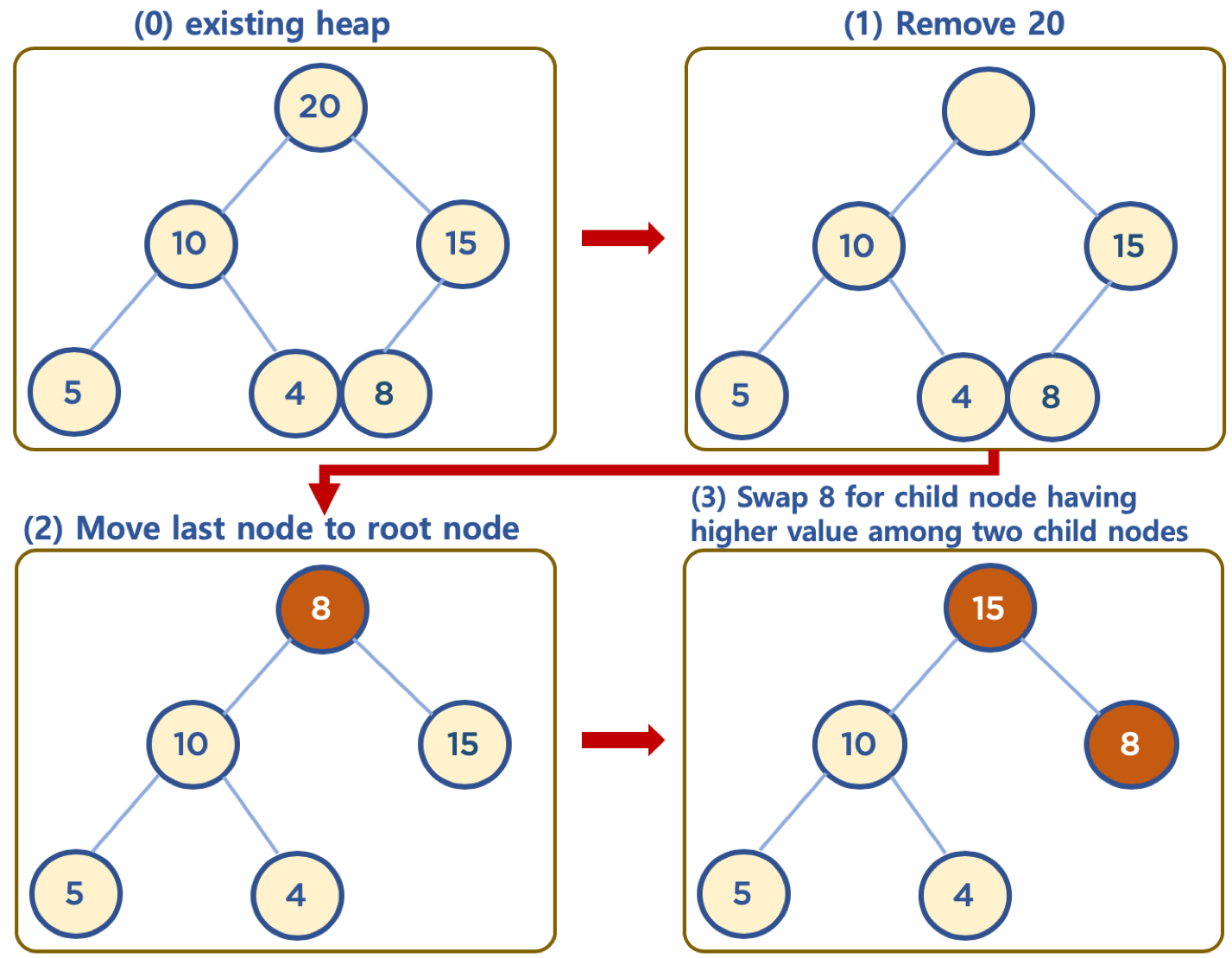
- 상단의 데이터 삭제시, 가장 최하단부 왼쪽에 위치한 노드 (일반적으로 가장 마지막에 추가한 노드) 를 root 노드로 이동
- root 노드의 값이 자식 노드보다 작을 경우, root 노드의 자식노드 중 가장 큰 값을 가진 노드와 root 노드 위치를 바꿔주는 작업을 반복함
힙(Heap) 주요 메서드
- insert() : Heap에 새로운 노드를 삽입합니다. 새로운 노드는 Heap의 마지막 노드에 위치
- delete() : Heap에서 루트 노드를 삭제합니다. 삭제 후, Heap의 마지막 노드를 루트 노드로 이동
- get_max()/get_min() : Heap에서 최대값 또는 최소값을 검색
- Heapify() : 일반적인 이진 트리를 Heap으로 변환
힙(Heap) 장단점
장점
- 빠른 삽입/삭제 연산 가능
- 우선순위 큐와 힙 정렬에 유용
단점
- 이진 탐색을 지원하지 않음
- 힙은 노드의 위치와 값이 무작위적으로 배치되어 있어 이진 탐색과 같은 탐색 연산을 지원하지 않는다.
- 메모리 사용량이 많을 수 있음
힙(Heap) 시간복잡도
- 삽입 : O(log n)
- 삭제 : O(log n)
- 최대/최소값 검색 : O(1)
- Heapify: O(n)
- n은 Heap에 저장된 노드의 개수입니다.
- Heap에서 삽입과 삭제 연산의 시간 복잡도는 O(log n)입니다. 이는 Heap의 높이가 log n 이하라는 것에서 유도됩니다. 또한 최대/최소값 검색은 루트 노드에 항상 위치하기 때문에 O(1)의 시간 복잡도를 가집니다.
- Heapify 연산은 일반적인 이진 트리를 Heap으로 변환하는 연산으로, 모든 노드를 순회하면서 부모 노드와 자식 노드 간의 힙 속성을 유지하는 과정을 거칩니다. 따라서 Heapify 연산의 시간 복잡도는 O(n)입니다.
복습해보기