가장 기본적인 방법은 itertools 라이브러리를 사용하는 것이다.
import itertools
itertools.permutations(iterable, r=len(iterable))
itertools.combinations(iterable, r)
사용하지 못할 때를 위해 직접 구현을 공부해보았다.
1. 순열(Permutation)
(1) 재귀 함수를 이용
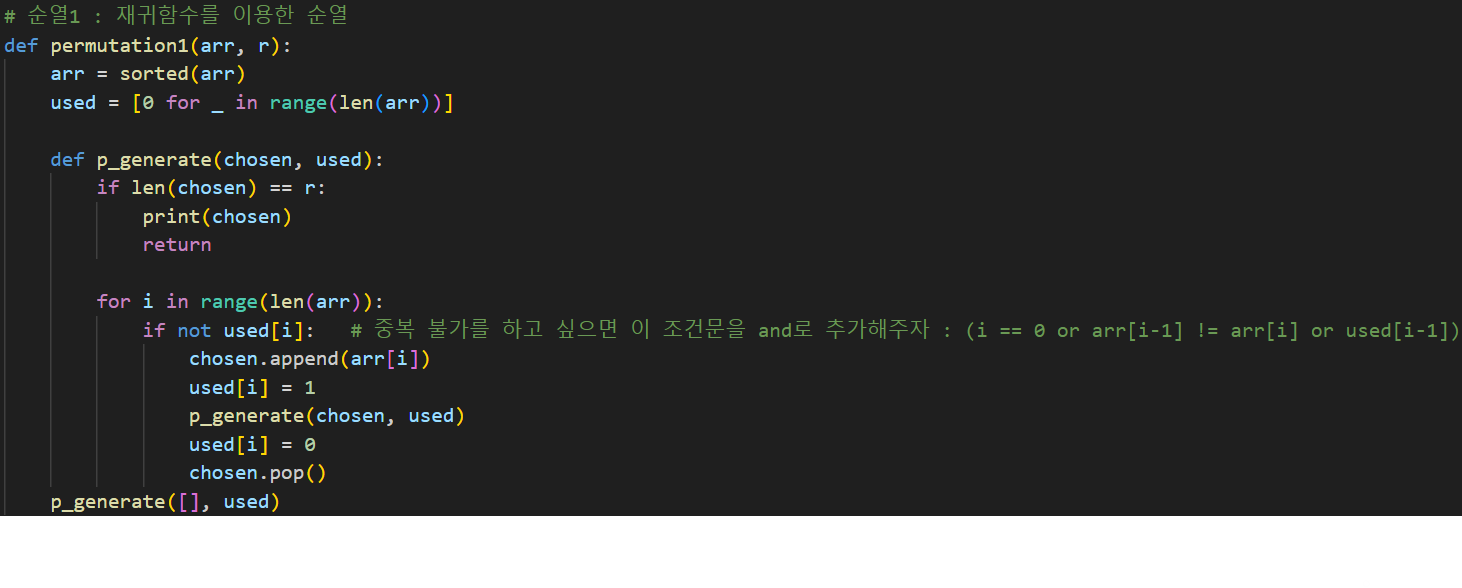
(2) 제네레이터를 이용(재귀 함수 사용)

(3) 위치 직접 바꿔주는 방식으로 구현

(4) 프로그래머스 level2 : 줄 서는 방법
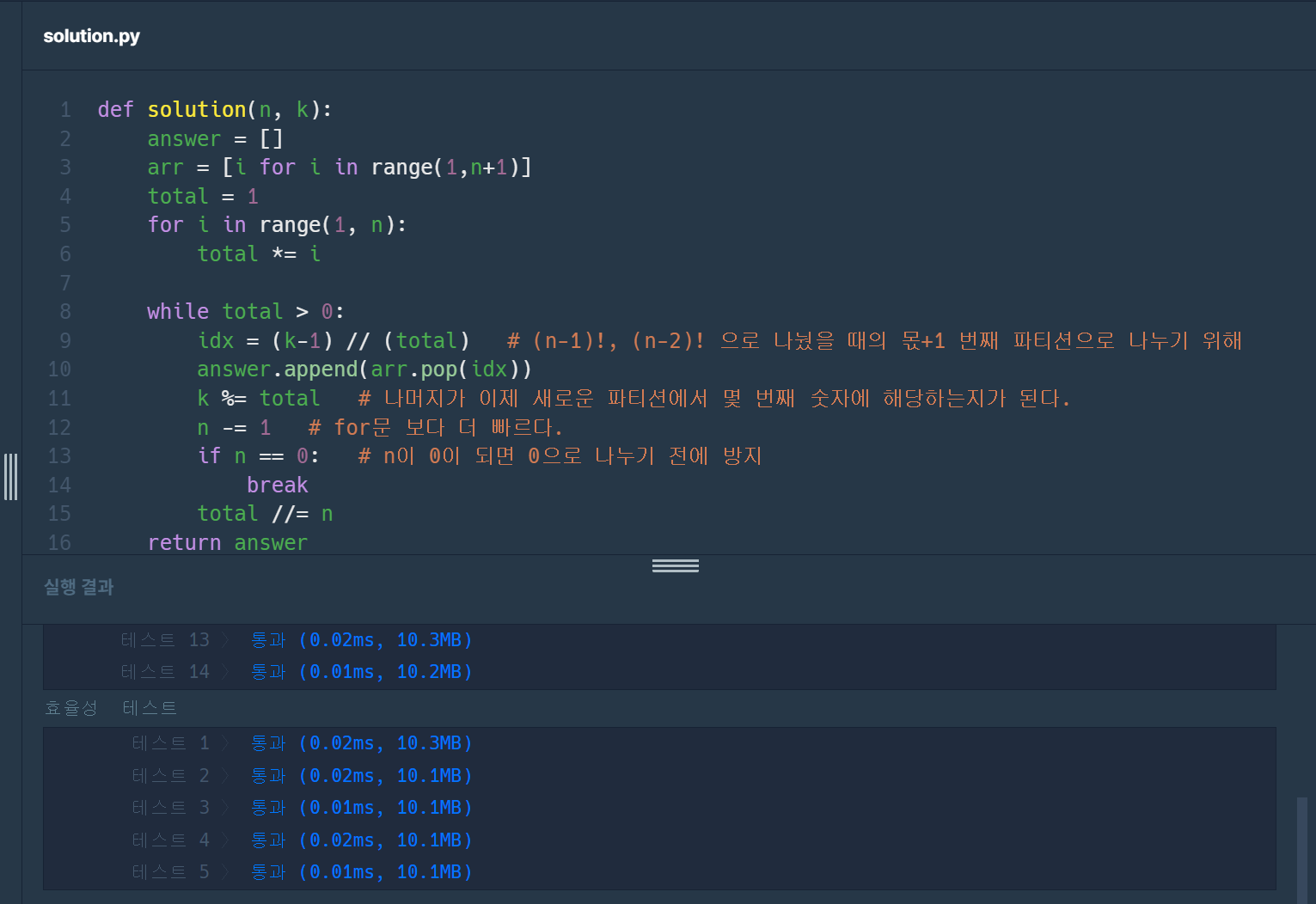

단순하게 순열을 사용하는 다른 방법들과 다르게 새로운 방법으로 풀어보았다. 또한, 연산 시간 최적화를 우선 순위로 풀어보았다.
n개의 단조 증가 수열로 정렬을 하고(1부터 n까지의 자연수가 아닐 때도 문제를 풀 수 있는 아이디어), 각각 몇 번 째 subclass(또는 partition)에 속하는지를 구해서 구할 수 있다.
예를 들어 12345는 첫 번째 subclass의 첫 번째 수, 21345는 두 번째 subclass의 첫 번째 수, 31254는 세 번째 subclass의 두 번째 수라고 볼 수 있다.
따라서, n진법으로 나타내는 방법과 유사하게 33을 4!, 3!, 2!, 1! 으로 나눴을 때의 몫과 나머지를 구해서 구하는 방법이다.
그림과 같이 33은 1을 빼고 4!으로 나눴을 때 몫이 1, 4!으로 나눴을 때의 나머지가 9이다.
이런 방식으로 n!을 구하는 과정에서 값이 커지는 것을 제외하면, 사칙연산 몇 번만 하면 돼서 효율성 테스트에서 모두 0.01ms대로 끝나는 것을 확인할 수 있다.
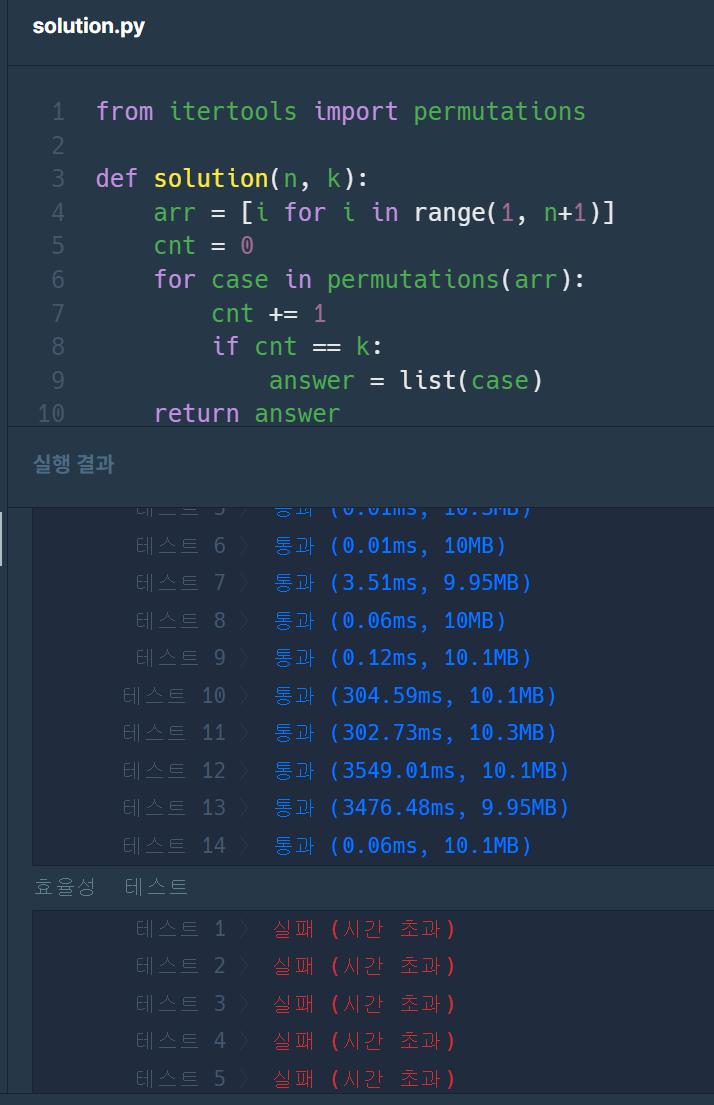
단순하게 순열을 사용하는 방법은 효율성 테스트 전에도 3000ms대로 무려 30만배 차이나는 것을 알 수 있다.
2. 조합(Combination)
(1) 재귀 함수를 이용
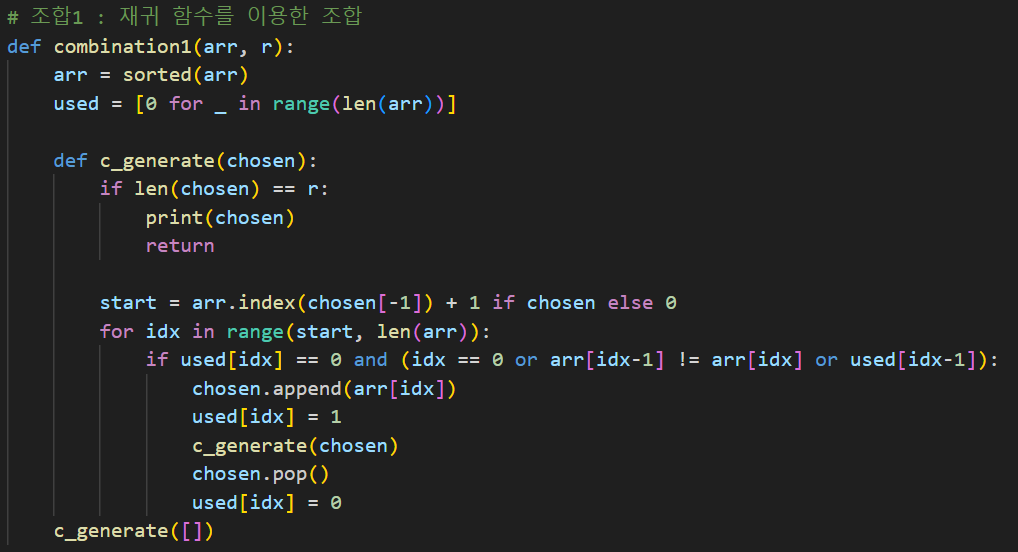
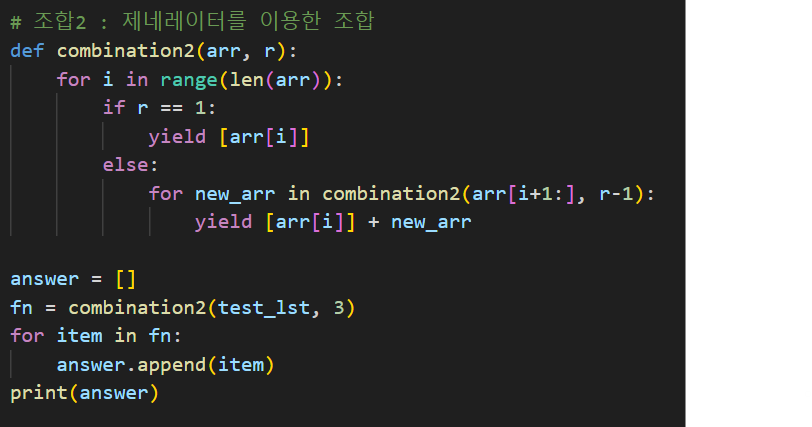
(2) 제네레이터를 이용(재귀 함수 사용)
https://shoark7.github.io/programming/algorithm/Permutations-and-Combinations