(시간 복잡도는 최선, 평균, 최악 순서)
(안정 알고리즘은 입력 순서를 유지하는 정렬 알고리즘)
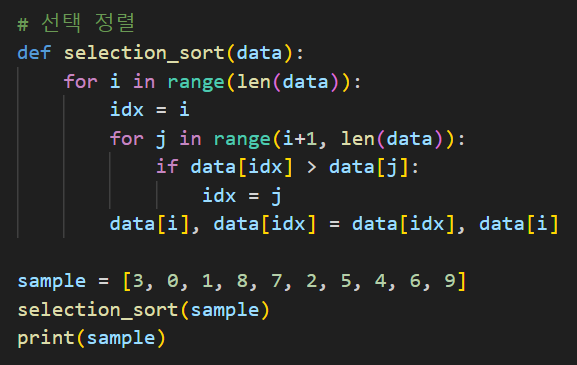
1. 선택 정렬
- 시간 복잡도 : O(n^2), O(n^2), O(n^2)
- 공간 복잡도 : O(1)
- 안정 : X
2. 삽입 정렬
- 시간 복잡도 : O(n), O(n^2), O(n^2)
- 공간 복잡도 : O(1)
- 안정 : O

3. 버블 정렬
- 시간 복잡도 : O(n^2), O(n^2), O(n^2)
- 공간 복잡도 : O(1)
- 안정 : O

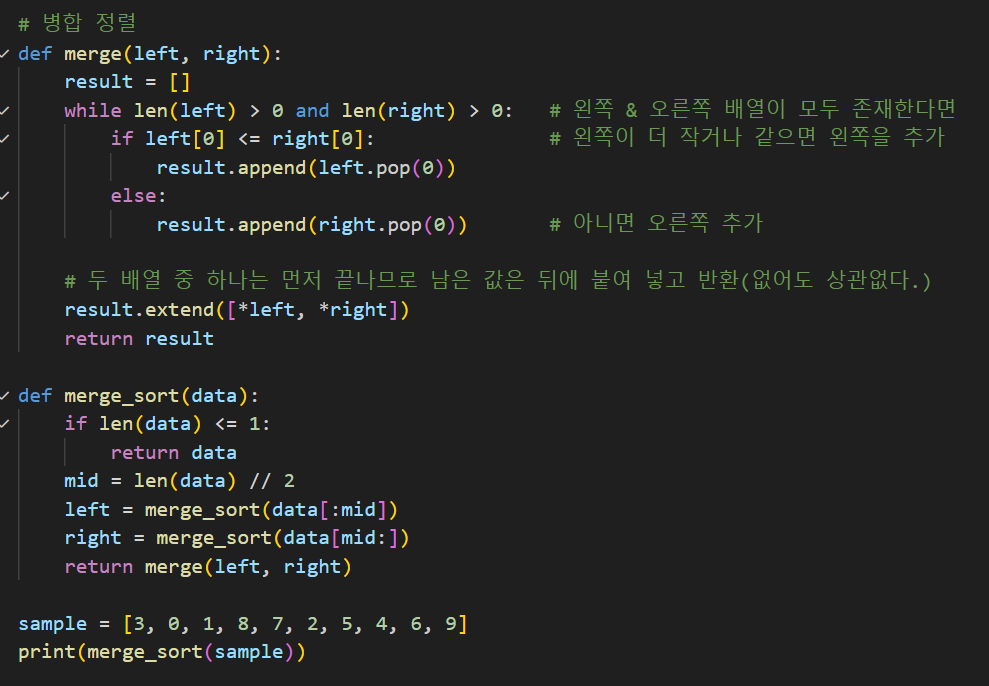
4. 병합 정렬
- 시간 복잡도 : O(nlogn), O(nlogn), O(nlogn)
- 공간 복잡도 : O(n)
- 안정 : O
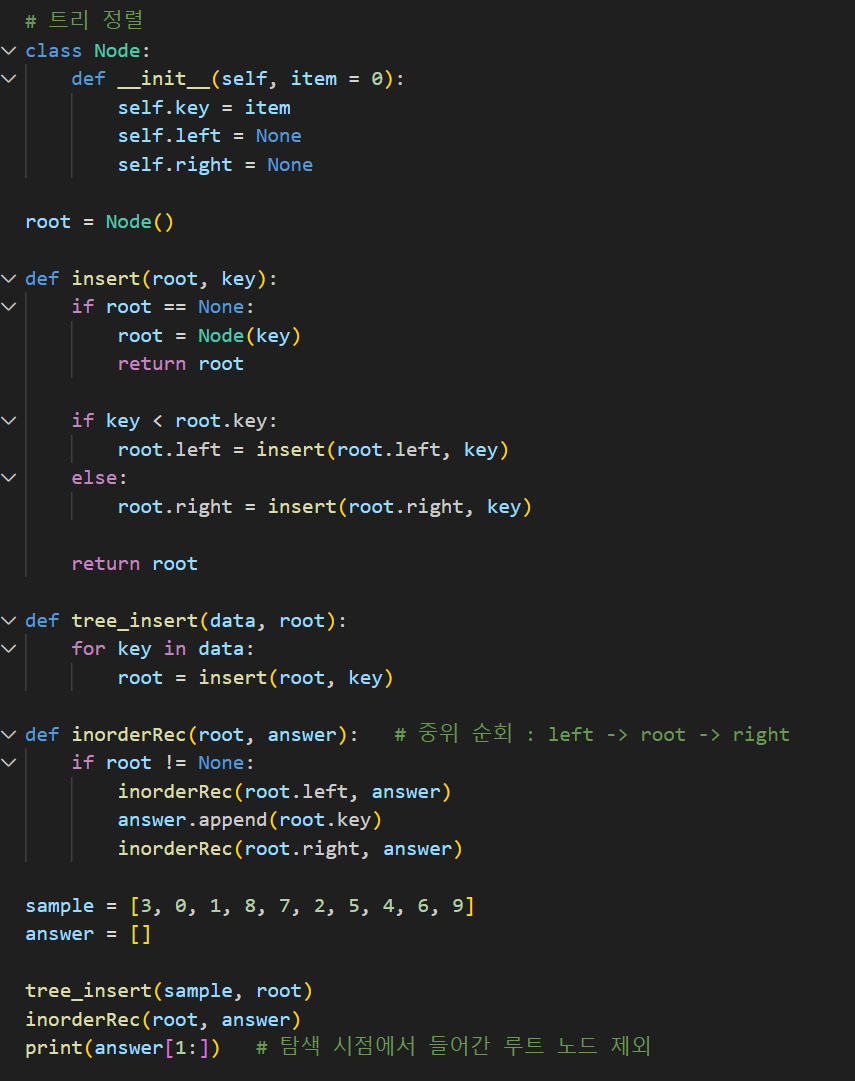
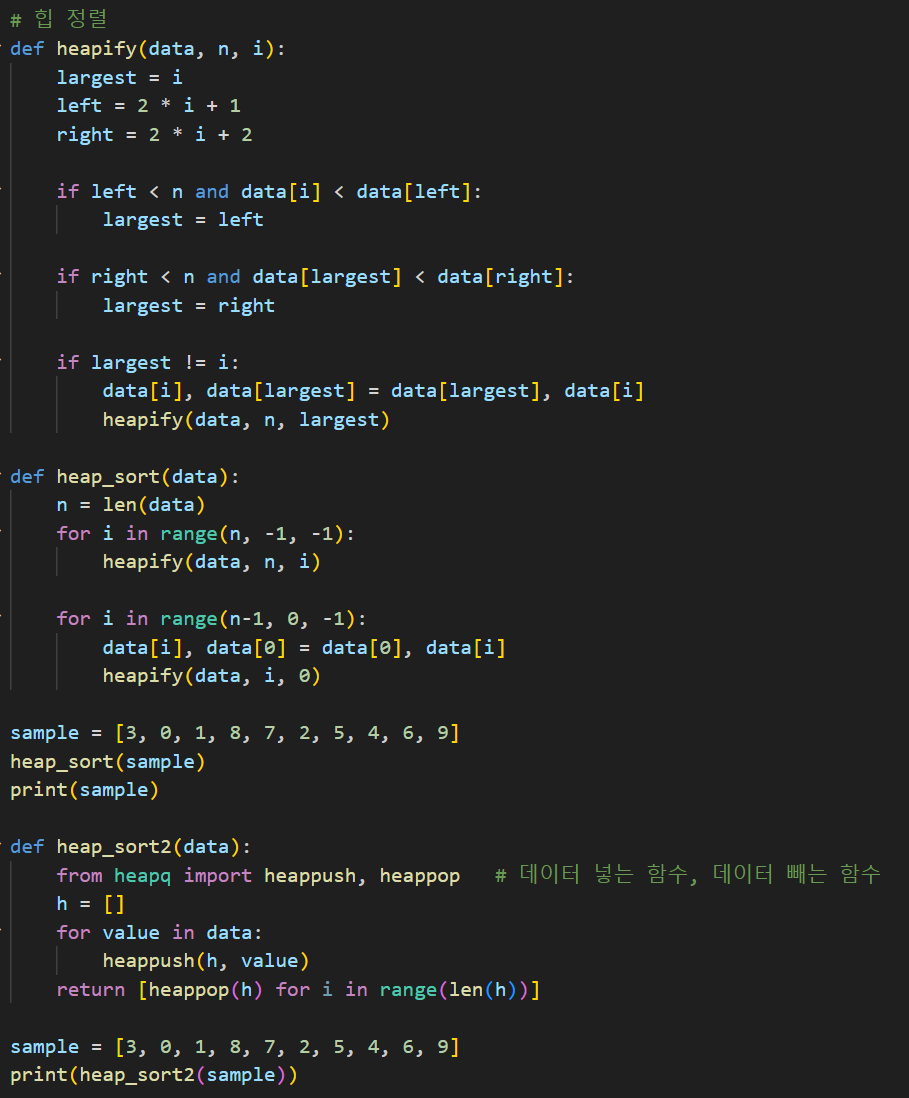
5. 힙 정렬
- 시간 복잡도 : O(nlogn), O(nlogn), O(nlogn)
- 공간 복잡도 : O(1)
- 안정 : X
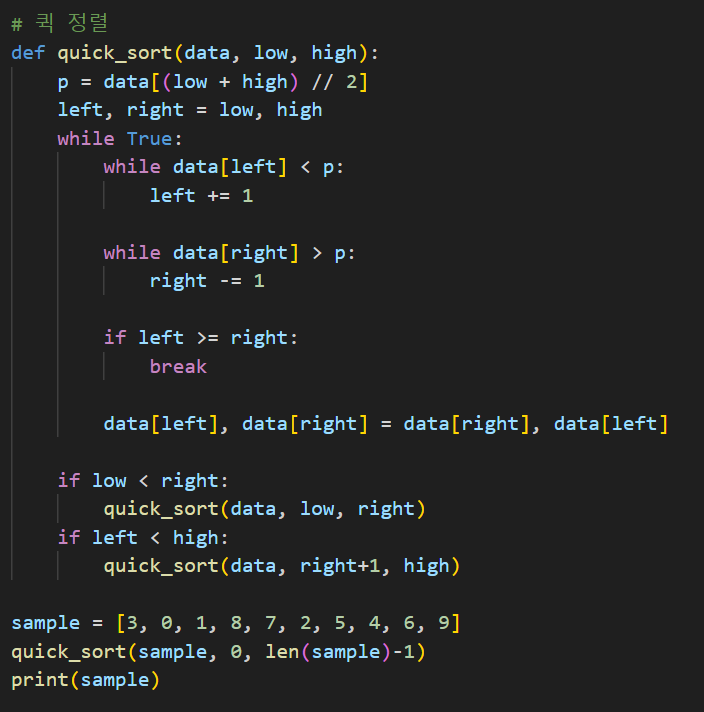
6. 퀵 정렬
- 시간 복잡도 : O(nlogn), O(nlogn), O(n^2)
- 공간 복잡도 : O(logn)
- 안정 : X
7. 팀 정렬(병합 정렬 + 삽입 정렬)
- 시간 복잡도 : O(nlogn), O(nlogn), O(nlogn)
- 공간 복잡도 : O(n)
- 안정 : O
개념
출처 : https://d2.naver.com/helloworld/0315536
TimSort는 2가지 아이디어로 정해졌다.
1. 현실 세계의 데이터들은 어느 정도 정렬된 상태일 것이다.
2. 그렇다면 정렬을 해야하는 전체 배열을 작게 자르고 각각 덩어리를 삽입 정렬로 정렬한 뒤 병합정렬로 병합하면 더 빠를 것이다.
정확한 시간 복잡도를 구하기 위해 참조 지역성(Locality of reference) 개념에 대해 알아야한다.
같은 시간 복잡도여도 C라는 상수가 곱해지고, 알고리즘 마다 C 값은 다르다.
이는 참조 지역성 때문이다.
참조 지역성 원리는 CPU가 미래에 원하는 데이터를 예측하여 속도가 빠른 장치인 캐시 메모리에 담아 놓는데 이때의 예측률을 높이기 위하여 사용하는 원리
최근에 참조한 메모리나 그 메모리와 인접한 메모리를 다시 참조할 확률이 높다는 이론을 기반으로 캐시 메모리에 담아놓는 것
힙정렬이 전체적으로 수치가 좋지만, 참조 지역성이 좋지 않다.
불안정 정렬이기도 하고, 절반 인덱스를 참조하는 방식이기 때문에 캐시 메모리에서 예측을 하기 어렵다.
퀵 정렬은 pivot 주변에서 데이터의 위치 이동이 많기 때문에 참조 지역성이 좋지만, 역시 불안정 정렬이고, 최악의 경우 O(n^2)의 시간복잡도를 가지기 때문에 탈락
O(nlogn)의 시간 복잡도를 가지고 있는 알고리즘 중 마지막인 병합정렬은 참조 지역성을 어느 정도는 만족하고, 입력 배열 크기 만큼의 메모리를 추가로 사용한다는 단점이 있지만 그렇게 많지는 않고, C의 값이 너무 커지지 않게 동작한다.
따라서 병합정렬과 삽입정렬을 합치게 된 듯 하다.
작동 원리 및 최적화
- 이진 삽입 정렬(Binary Insertion Sort)
먼저 덩어리의 크기가 min(N, 2^5 또는 2^6)가 될 때 까지 이진 삽입 정렬을 한다.
(적당히 작은 n값)
(실제 데이터는 어느 정도 정렬이 되어있다고 가정했기 때문에 정렬되어있다는 전제로 이진 삽입 정렬)
(subset의 크기가 32이고 개수가 34인게 subset의 크기가 34이고 개수가 32인 것 보다 빠르기 때문에 2의 거듭제곱 꼴로 만든다.)
가장 처음 두 수가 증가하면 그 subset(덩어리)은 증가하는 subset으로 가정하고 문제를 진행한다.
(증가하는 subset, 감소하는 subset을 표시해둔다.)
subset의 크기가 지정한 크기(2^5 또는 2^6)가 될 때 까지 뒤의 원소에 대해 BIS를 진행한다.
해당 크기가 됐을 때, subset의 크기를 최대한 크게 하기 위해 증가(또는 감소)하는 동안에는 subset에 계속 원소를 추가해준다.
이때 추가적으로 증가하는 subset에서는 같은 원소도 증가한다고 계산하지만,
감소하는 subset은 같은 원소가 나오면 종료하고 뒤집는다.
이후에 같은 원소부터 다시 subset을 만들기 시작한다.
이는 Tim Sort는 안정 정렬이어야 하고, 뒤집을 경우 동일한 원소의 순서가 뒤집혀서 이를 방지하기 위해서다.
- 병합 정렬(Merge Sort)
두 subset을 병합하여 정렬된 하나의 subset으로 만드는 과정에서 n의 추가 메모리와 두 subset의 크기의 합 만큼의 시간이 필요하다.
또한, 안정성을 유지하기 위해 인접한 subset에 대해 병합을 진행해야하고,
비슷한 크기의 subset과 병합할 때 효율이 좋다.
그러나 Tim Sort의 경우 subset들의 크기가 다 다르다.
따라서 다음과 같은 방법을 사용한다.
먼저 subset을 stack에 쌓는다.
이때, 2가지 조건을 만족해야한다.
- 아래 있는 subset의 길이가 커야한다.
- 위의 두 subset 길이의 합보다 아래의 subset의 길이가 커야한다.
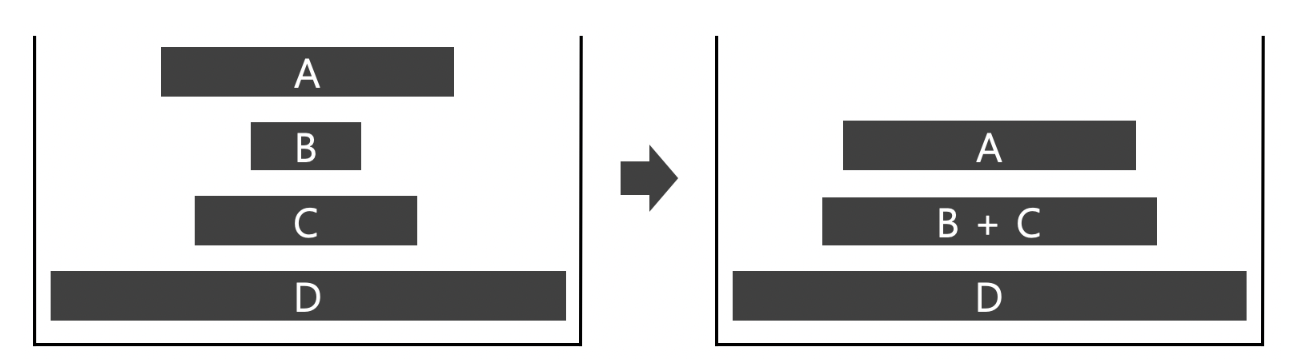
따라서 위의 그림 같은 경우, A가 들어오는 순간 조건을 만족하지 않게 되고,
B는 A와 C중 작은 subset과 병합된다.
조건을 만족할 때 까지 진행해야하므로, B+C는 A와 병합이 진행된다.
이 결과로 stack에 들어있는 subset의 개수는 작게 유지될 수 있고, 그나마 비슷한 크기의 덩어리와 병합할 수 있다.
그 다음 메모리의 효율을 살리기 위해 다음과 같은 방법을 사용한다.
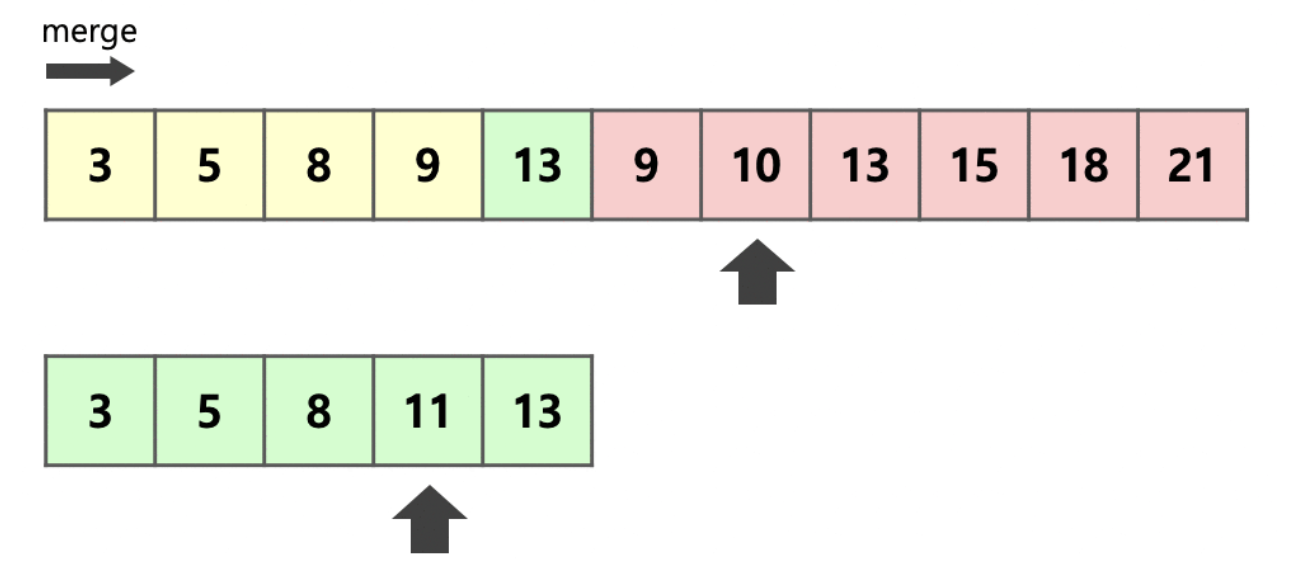
작은 subset(초록색)과 큰 subset(빨간색)이 있을 때, 작은 subset을 복사한다.
이후, 원래 메모리에 원소를 수정하는 방식으로 작동하고, two pointer를 이용하여 삽입할 때 마다 한 칸씩 이동한다.
이 결과로 겹치지 않게 삽입이 가능하다.
빨간색 subset이 작을 경우 이번에는 가장 오른쪽에 two pointer를 두고 왼쪽으로 진행하며 감소할 때 삽입을 진행하고 pointer를 이동시키는 방법을 사용한다.
(같은 값이 나올 때는 항상 안정 정렬 고려)
이때, 한 단계 더 최적화를 진행하기 위해 정렬하지 않아도 되는 구간을 계산한다.
위의 그림의 경우 초록색 subset 중 빨간색 subset의 가장 작은 값(9)보다 작은 값들은 확인할 필요가 없다.
또한, 빨간색 subset 중 초록색 subset의 가장 큰 값(13)보다 큰 값들은 확인할 필요가 없다.
(양쪽 left 2개를 비교해서 둘 중 큰 값 보다 작은 값들은 고려하지 않는다.
그리고, 양쪽 right 2개를 비교해서 둘 중 작은 값보다 큰 값들은 고려하지 않는다.)
물론, 이는 이분 탐색으로 진행한다고 해도 계산을 추가로 필요로 하고, 만약 고려하지 않아도 되는 구간이 없다면 괜한 시간만 더 들게 되는 것이다.
그렇지만, 실제 데이터에서 많은 상황에 이득을 볼 수 있기 때문에 이러한 최적화를 추가한 것으로 보인다.
마지막으로 Galloping(급속도로 진행하는 것) 이라는 최적화 방법을 사용한다.
병합 단계의 two pointer에서 하나의 subset의 pointer가 바뀌지 않고 나머지 subset의 pointer만 3번 연속으로 진행되는 경우, Galloping mode가 진행된다.
한 칸씩 이동 하는 것이 아니고, 연속될 때 마다 이동 거리를 2배씩 늘리는 것.
즉, 1칸, 1칸, 1칸, 2칸, 4칸, 8칸, ...
이런식으로 이동한다.
그러다 멈추게 되면, 일반 mode로 변화되고 그 사이의 구간을 이분 탐색한다.
여기에서 기준 값(MIN_GALLOP)은 3으로 고정된 값이 아니고, 전체 배열을 정렬하는 과정에서 Galloping mode에 들어가는 횟수가 많았다면 더 자주 실행되게 하기 위해 감소하고, 들어가는 횟수가 적었다면 값을 증가시키는 방법을 사용하여 좀 더 효율적으로 작동하게한다.
8. 파워 정렬(Python 3.11)
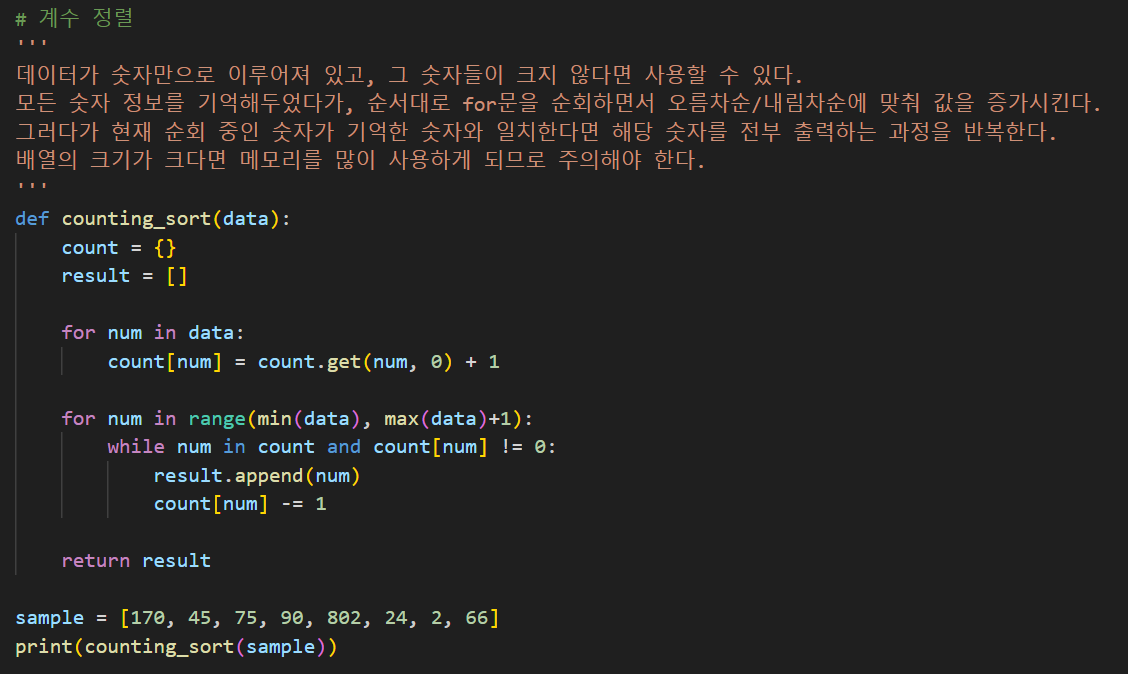
9. 계수 정렬
10. 기수 정렬
