[Algorithm] 5. 최소 신장 트리

개념

이번에는 최소 신장 트리(Minimum Spanning Tree)에 대해 알아본다.

Spanning Tree
그래프 내의 모든 정점을 포함하는 트리이다.
즉, 그래프의 최소 연결 부분 그래프이다.
n개의 정점을 가지는 그래프의 최소 간선의 수는 n-1이다.
역으로, n개의 정점이 n-1개의 간선으로 연결되어 있으면 필연적으로 트리 형태가 되고, 이것이 바로 Spaaning Tree가 된다.(사이클을 포함하면 안된다.)

Minimum Spanning Tree
Spanning Tree 중 사용된 간선들의 가중치의 합이 최소인 트리

즉 n개의 노드를 전부 연결하는 간선의 최소 개수는 n-1개이고, 최소 비용은 n-1개의 간선을 사용했을 때 발생할 수 밖에 없다.

구현

노드가 n개이고, 간선이 e개라면, Kruskal의 시간 복잡도는 O(eloge)이고,
Prim의 시간 복잡도는 O(n^2)이기 때문에, 적은 간선을 가지는 희소 그래프(Sparse Graph)의 경우 Kruskal이 적절하고, 간선이 많은 밀집 그래프(Dense Graph)의 경우는 Prim 알고리즘이 적절하다.
프로그래머스 lv3 : 섬 연결하기 문제를 2가지 방법으로 풀어보자.
간선이 최대 n*(n-1)/2 까지 될 수 있으므로, Prim 알고리즘을 선택.
(그러나 실제로 연결을 많이 안담고있는지 Prim 알고리즘의 시간이 좀 더 소요된 것을 확인할 수 있다.)

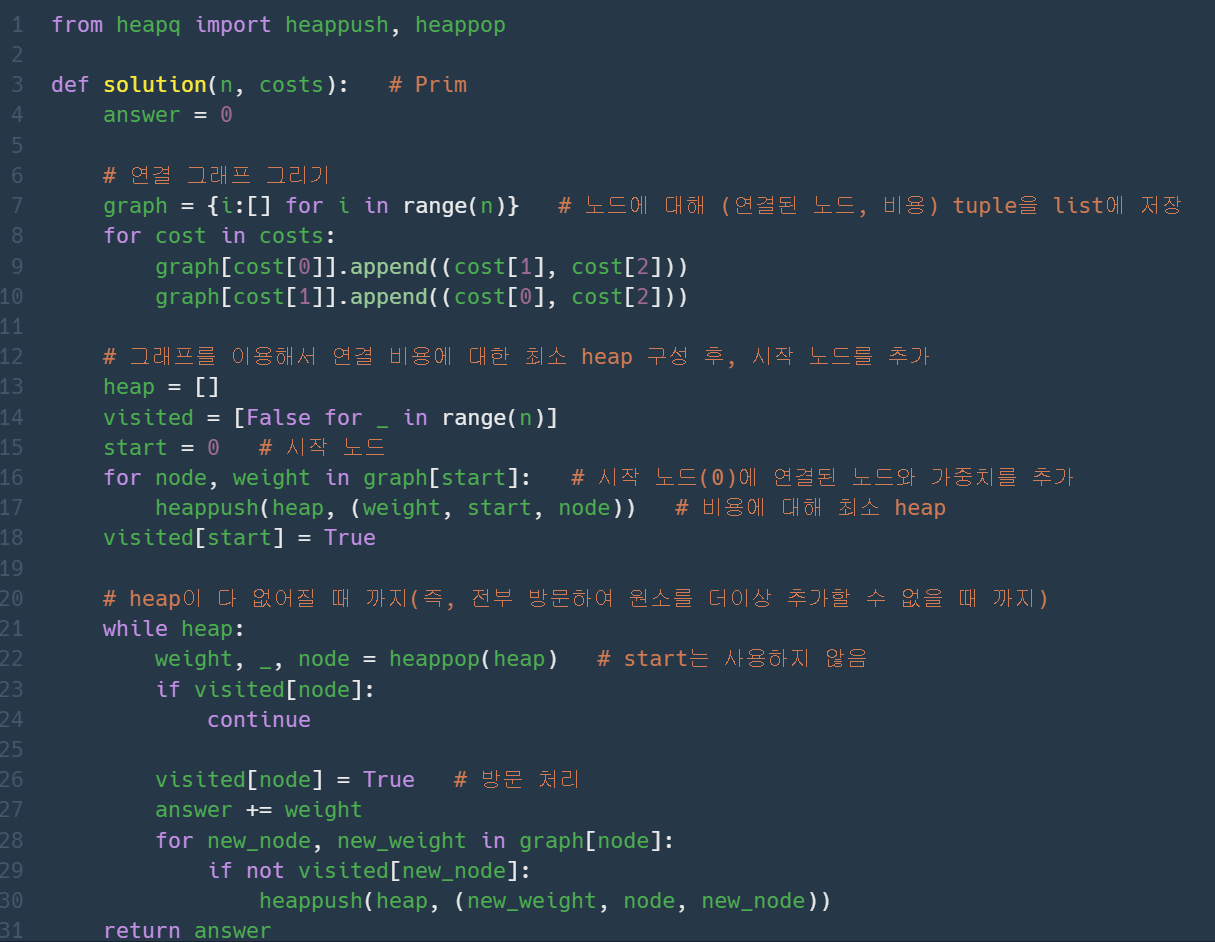
Prim Algorithm

탐욕법(Greedy Method) 중 하나로, 모든 간선을 확인하는 것이 아닌, 노드와 연결된 간선을 확인하여 방문하지 않은 노드와 연결된 간선 중 최소 비용 간선을 추가한다.
(이는 n-1개의 간선이 최소 신장 트리를 구성한다는 점을 이용하는 것. 즉, 모든 노드는 한 번씩만 추가돼야한다.)
따라서, 각 노드별로 어떤 노드가 연결되었는지에 대한 정보가 있는 그래프를 만들고 시작해야한다.
그리고 첫 번째 시작점을 기준으로 시작점과 연결된 노드들을 가중치에 대해 오름차순으로 heap에 넣는다.
그리고, 이미 방문한 연결 노드들은 제외하고, 방문한 적 없으면 그 노드를 연결한다고 생각하고 비용에 가중치를 추가하고, 그 노드를 시작점으로 하는 연결 정보들도 heap에 추가한다.
그리고 시작 노드에서 여러 연결이 될 수 있으므로, 초기화하지않고 비용이 최저인 것 중 노드를 추가하는 것만 생각한다.

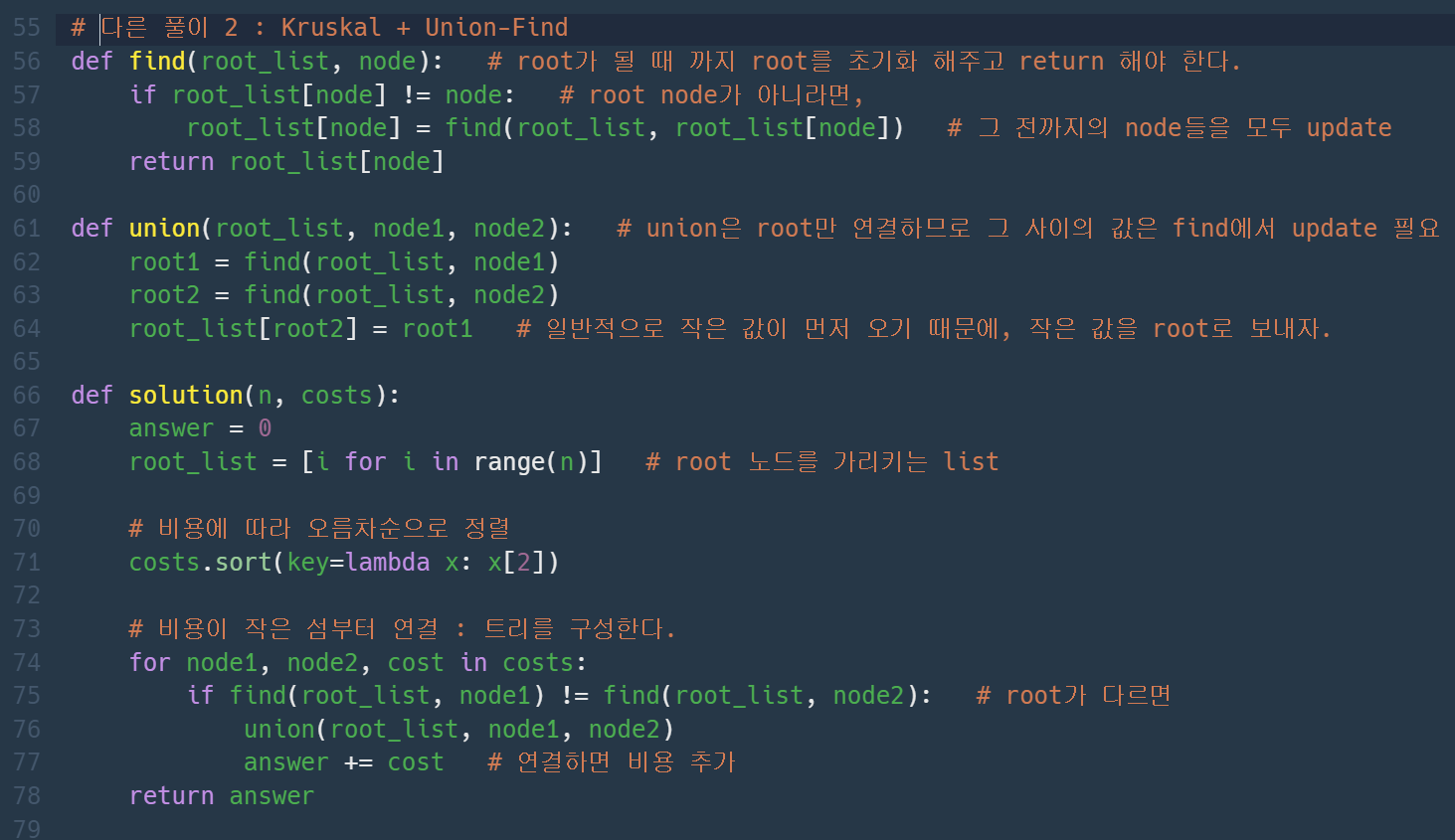
Kruskal Algorithm

역시 탐욕법(Greedy Method) 중 하나로 그래프의 정점을 최소 비용으로 연결하는 최적 해답을 구하는 것.
최소 비용의 간선으로 구성된다.
사이클을 포함하지 않는다.
이 2가지를 확인하는 방식으로 사이클을 생성하지 않는 간선들을 확인하여, 그 중 최소 비용인 간선을 추가한다.
Union-Find Algorithm을 이용한다.
이는, 두 개의 노드를 비교해서 각각의 부모를 비교하고, 이를 통해 같은 집합(그래프)에 속하는 지 확인하는 알고리즘이다. 즉, Disjoint Set을 만든다.

• set과 dict의 원소 추가 방법
  

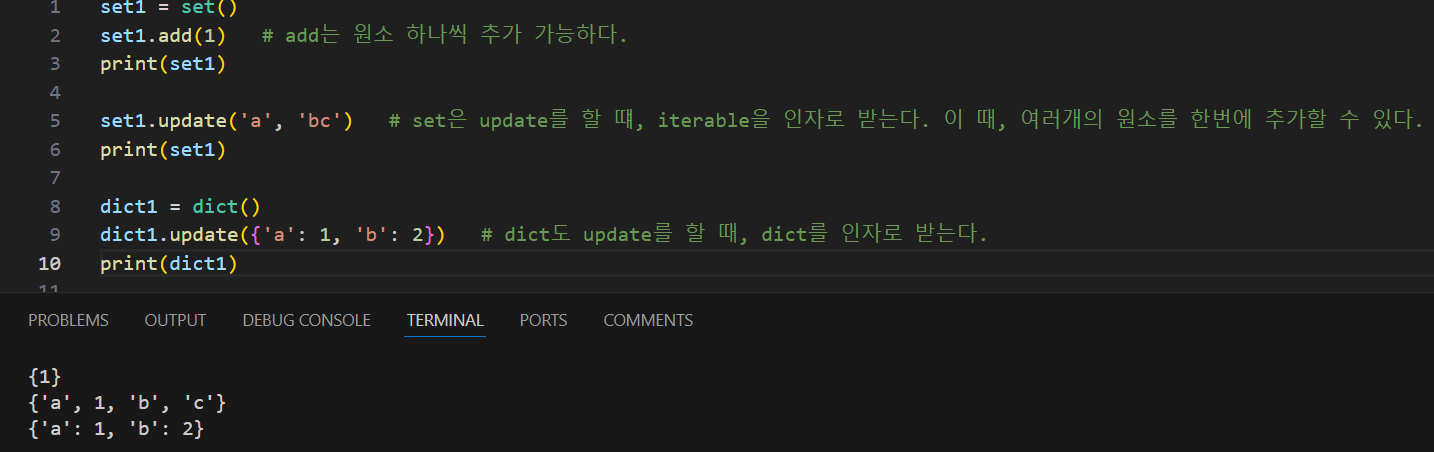
• 모든 간선을 확인하는 방법(Union Find를 사용하지 않는 방법)
  
  

• 모든 간선을 확인하는 방법(Union Find를 사용하는 방법)