Evaluate Classifier

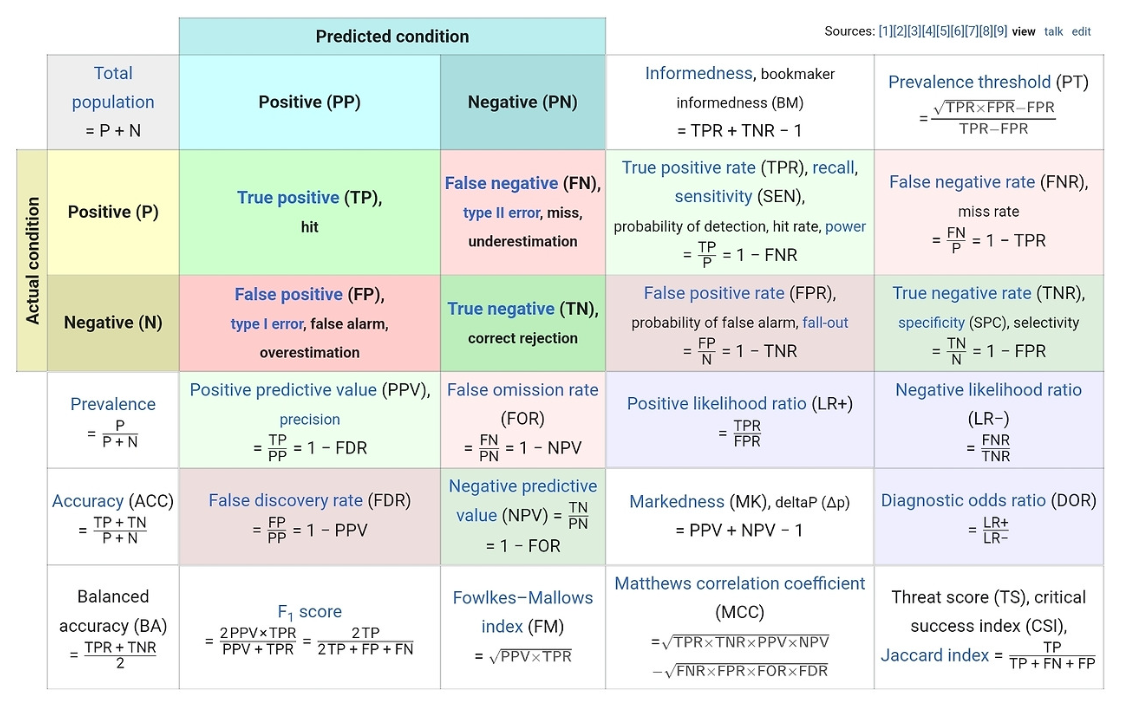
출처 https://en.m.wikipedia.org/wiki/Template:Diagnostic_testing_diagram

True Positive(TP) : 양성을 양성으로 예측

True Negative(TN) : 음성을 음성으로 예측

False Positive(FP) : 음성을 양성으로 예측(type1 error)

False Negative(FN) : 양성을 음성으로 예측(type2 error)

• Accuracy(정확도)

  전체 개수 중 정답을 맞춘 개수

  $ACC = \frac{TP + TN}{TP + TN + FP + FN}$

• Sensitivity(민감도) / Recall(재현율)

  실제 양성을 양성으로 예측한 비율(True Positive Rate)

  $TPR = \frac{TP}{TP + FN}$

• Specificity(특이도)

  실제 음성을 음성으로 예측한 비율(True Negative Rate)
  $TNR = \frac{TN}{TN + FP}$

• Positive Predictive Value(양성예측도) / Precision(정밀도)

  양성이라고 예측한 값들 중 실제 양성의 비율

  $PPV = \frac{TP}{TP + FP}$

• Negative Predictive Value(음성예측도)

  음성이라고 예측한 값들 중 실제 음성의 비율

  $NPV = \frac{TN}{TN + FN}$

• F1 Score(Precision과 Recall의 조화 평균)

  $\dfrac{2}{\dfrac{1}{Precision} + \dfrac{1}{Recall}}$

• Macro-Averaged F1 Score

  다중 분류에서는 클래스가 여러개(n) 있고, 단순하게 모든 클래스에 대한 F1 Score의 평균을 구하는 방법이다.
  즉, 클래스 또는 라벨의 중요도가 다를 때는 적절하지 않을 수 있다.

  $\frac{\textstyle\sum_{i=1}^n F1\;Score_i}{n}$

• Weighted F1 Score

  각 클래스 별로 다른 가중치를 주어 F1 Score의 가중합을 구하는 방법이다.
  (여기서 $w_i$는 총 샘플의 개수 중 해당 클래스에 속하는 샘플의 개수이다.)

  $\frac{\textstyle\sum_{i=1}^n w_i * F1\;Score_i}{n}$

• Micro-Averaged F1 Score

  
  
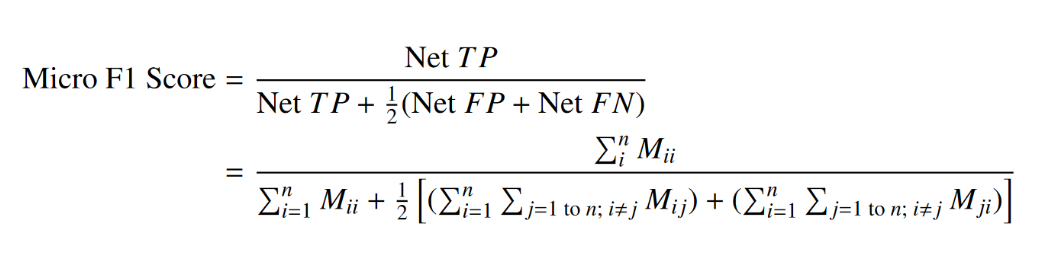
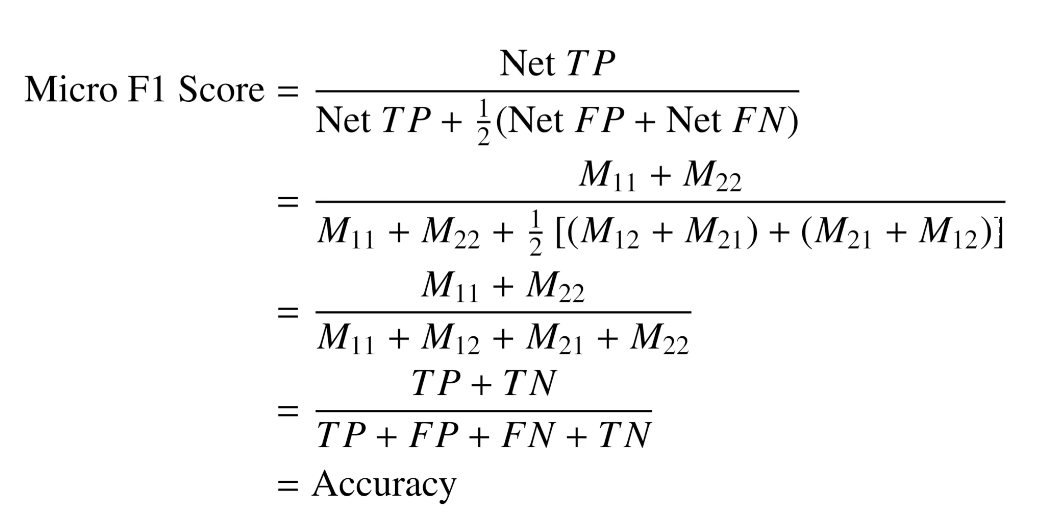
  출처 : https://www.v7labs.com/blog/f1-score-guide#how-to-compute-f-measures-in-python

score를 구하고 평균내는 방식이 아닌 처음부터 나눠서 계산하는 방법이다.
클래스 별로 n번의 F1 Score를 구하는 방식이 아닌 nxn 크기의 혼동 행렬 M을 만들고, ij 번째 성분에 실제값 i를 j로 예측한 개수를 넣는다.
그리고 마지막으로 i를 i로 예측한 n개의 대각 성분 값의 합을 분자로 전체 개수를 분모로 하는 값을 만든다.
FP와 FN이 같기 때문에 Accuracy, Micro-Precision, Micro-Recall 이 모두 같음을 알 수 있다.

• $F\beta\;Score$

  $\frac{1 + \beta^2}{\dfrac{1}{Precision} + \dfrac{\beta^2}{Recall}}$

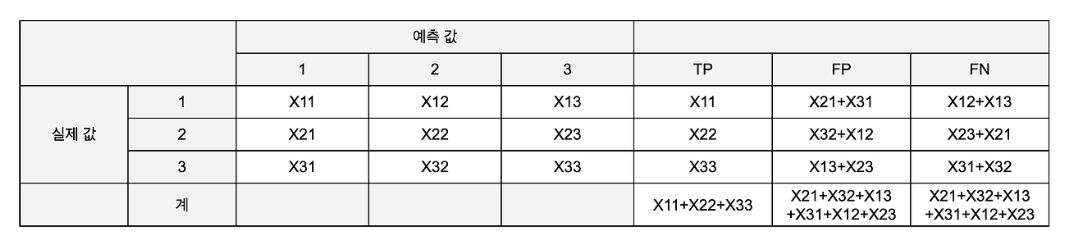
• Precision-Recall Curve(PRC)

  x축을 Recall y축을 Precision 으로 하는 xy 평면에서 분류기의 threshold에 따라 점을 찍었을 때 생기는 곡선(그래프)
  무작위 예측은 50:50으로 예측한다는 의미이고, Precision에서 분모가 샘플의 1/2이다. 즉, 예측과 무관하게 양성과 음성의 비율에 따라 Precision은 커지고 작아지고 할 것이기 때문에, 무작위 예측의 그래프는 양성의 비율에 따라 커지고 작아지는 Recall 축과 평행하게 그려진다.

• Area Under The Precision-Recall Curve(AUPRC)

  PRC의 아래 면적을 구한 것으로, Recall의 범위가 0~1이기 때문에 PRC의 아래 면적은 Precision의 평균(AP)과 같다. 곡선에서 Recall을 같은 간격으로 나눠 그 지점에서 Precision을 측정하고 해당 값을 기준으로 넓이를 구하는 방법으로 곡선 아래의 면적을 편하게 구할 수 있다.

• Receiver Operating Characteristic(ROC)

  PR 그래프에서 R이 증가할 때, P가 단조감소한다. 따라서 단조증가(우상향) 그래프를 만든 것이라고 이해했다.
  ROC 곡선의 x축은 FPR(1-Specificity) y축은 TPR(Sensitivity)이다.

• Area Under The ROC Curve(AUC or AUROC)

  AUPRC와 같이 아래 면적을 구하고 그 면적값을 AUC 값으로 한다. 최대 넓이는 1이므로 최대값이 1이다. 무작위 예측을 하면 y = x 아래 면적에 해당하기 때문에 1/2 보다 작으면 무작위 예측보다 못한 분류기이다.