2024-05-09
오일러 각 (Euler's angle)
3차원 공간에서 물체가 놓인 방향을 3개의 각을 사용해 표시하는 방법
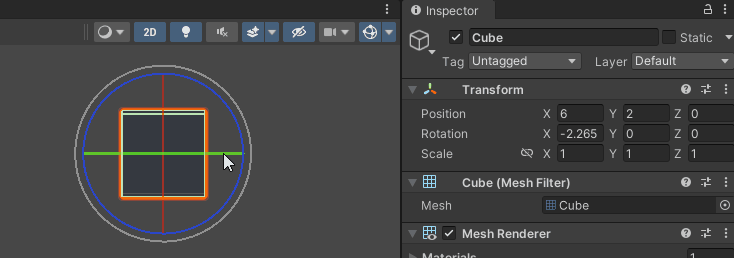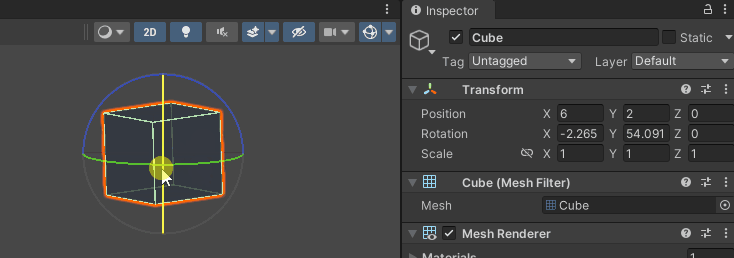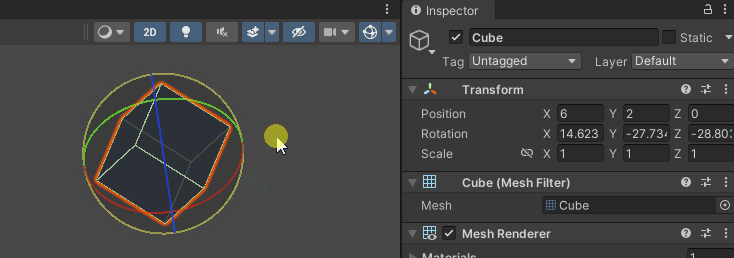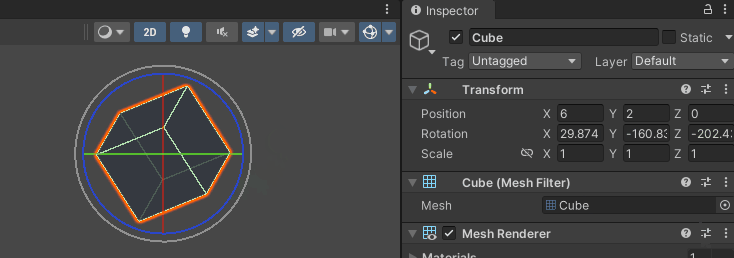
Rotation X, Y, Z 값은 실수이기 때문에, Vector3 를 사용해 관리할 수 있다.
소프트웨어(언리얼, Unity ... ) 마다, x,y,z 축의 용도가 다르기 때문에,
오일러 각 정보를 그대로 전달하여 사용할 수 없다.
( X : Red, Y : Green, Z : Blue , 선택한 축 : Yellow 로 구분)
따라서, x,y,z 축 대신 회전의 움직임으로 회전 동작을 구분하고 각을 지정하는 방법이 사용된다.
요, 롤 , 피치
항공기의 회전을 표현할 때 사용하는 용어로, 게임에서도 사용된다.
| 회전 | 방향 | 축 |
|---|---|---|
| 요(Yaw) | 위 | y |
| 롤(Roll) | 앞 | z |
| 피치(Pitch) | 오른쪽 | x |
오일러 각의 장점
- 직관적인 인터페이스를 제공
- 적은 용량으로 3차원 공간의 회전 정보를 기록
- 행렬을 사용해 3차원 공간의 회전을 표현 - 최소 9개의 실수 데이터 필요
- 오일러 각을 사용해 3차원 공간의 회전을 표현 - 3개의 데이터
오일러 각의 단점 - 짐벌락(Gimbal Lock)
짐벌
하나의 축을 중심으로 물체가 회전할 수 있도록 만들어진 구조물.
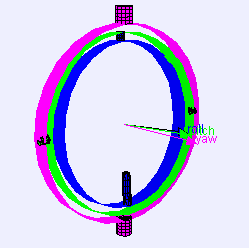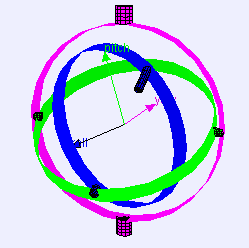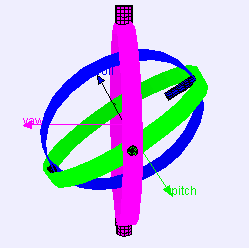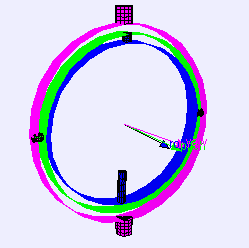
가장 바깥쪽 고리는 고정된 축으로 회전하지만,
안쪽 고리들은 여러 방향으로 회전할 수 있다.
짐벌락의 발생 조건
이때, 고리의 회전으로 두 개 이상의 고리가 겹치게 되면 (축이 같아지면),
한 축의 회전각이 소실된다.
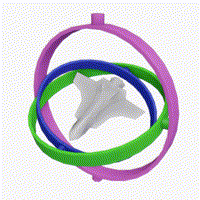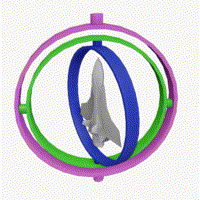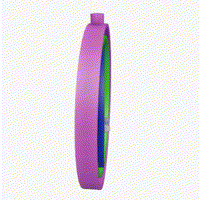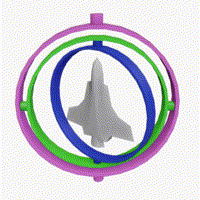
Unity 의 인스펙터 창에서는 오일러 각으로 표현하고 있지만, 내부적으로 쿼터니언 방식을 통해 방향을 표현한다.
개발자가 의도적으로 오일러 각을 고정하지 않는다면, 짐벌락은 발생하지 않는다.
3차원 공간의 회전
오일러 각 방식에서는 3차원 공간의 회전을 3번에 나눠 진행한다.
Unity 의 경우, Z축 -> X축 -> Y축 순서로 오일러 회전이 진행되는데,
실시간으로 변화하는 동적인 3차원 회전을 구현할 때, 짐벌락이 발생할 수 있다.
사원수 (Quaternion)
4개의 독립된 체계로 구성된 4차원의 수집합
(복소수에서 2차원의 복소 평면을 4차원 공간으로 확장한 개념)
유니티에서 제공하는 사원수와 관련된 메서드를 활용하여,
오일러 각의 문제인 짐벌락을 해결할 수 있다.
Quaternion.Euler
x, y, z 에 오일러 각을 넣으면 쿼터니언으로 변환된 값을 반환해준다.
public static Quaternion Euler(float x, float y, float z);Quaternion.LookRotation
forward 벡터를 upwards 벡터를 바라보게 회전시키는 쿼터니언 값을 반환한다.
public static Quaternion LookRotation(Vector3 forward, Vector3 upwards = Vector3.up);upwards 의 디폴트 값은 Vector3.up 으로,
일반적으로 머리가 향하는 방향은 월드 좌표의 위쪽을 향한다고 생각하자.
Quaternion.Slerp
a 와 b 사이를 t 로 구형 보간한 값을 반환한다.
public static Quaternion Slerp(Quaternion a, Quaternion b, float t);Slerp
구형 보간(Slerp : SPherical Linear Interpolation)
오브젝트를 부드럽게 회전시킬 때 사용된다.
Lerp 의 경우, 두 점 사이 직선을 t 로 보간한 값을 반환하지만,
Slerp 의 경우, Lerp 를 3차원 공간으로 확장하여 보간 결과로 만들어지는 방향을 반환한다.
arc-tangent
탄젠트의 역함수.
가로-세로의 비율 을 통해 각도를 계산하는 데 사용된다.
Math.Atan
가로 세로 비율을 통해 라디안 값을 구할 수 있다.
[-π/2 , π/2] 의 라디안 값으로 반환)
public static float Atan (float f);문제점
아래 그림의 θ 와 θ' 는 다른 각도지만,
Atan(b/a) 과 Atan(-b/-a) 는 같은 θ 를 반환한다.
이를 구별하기 위해 한 가지의 함수를 더 추가하였다.
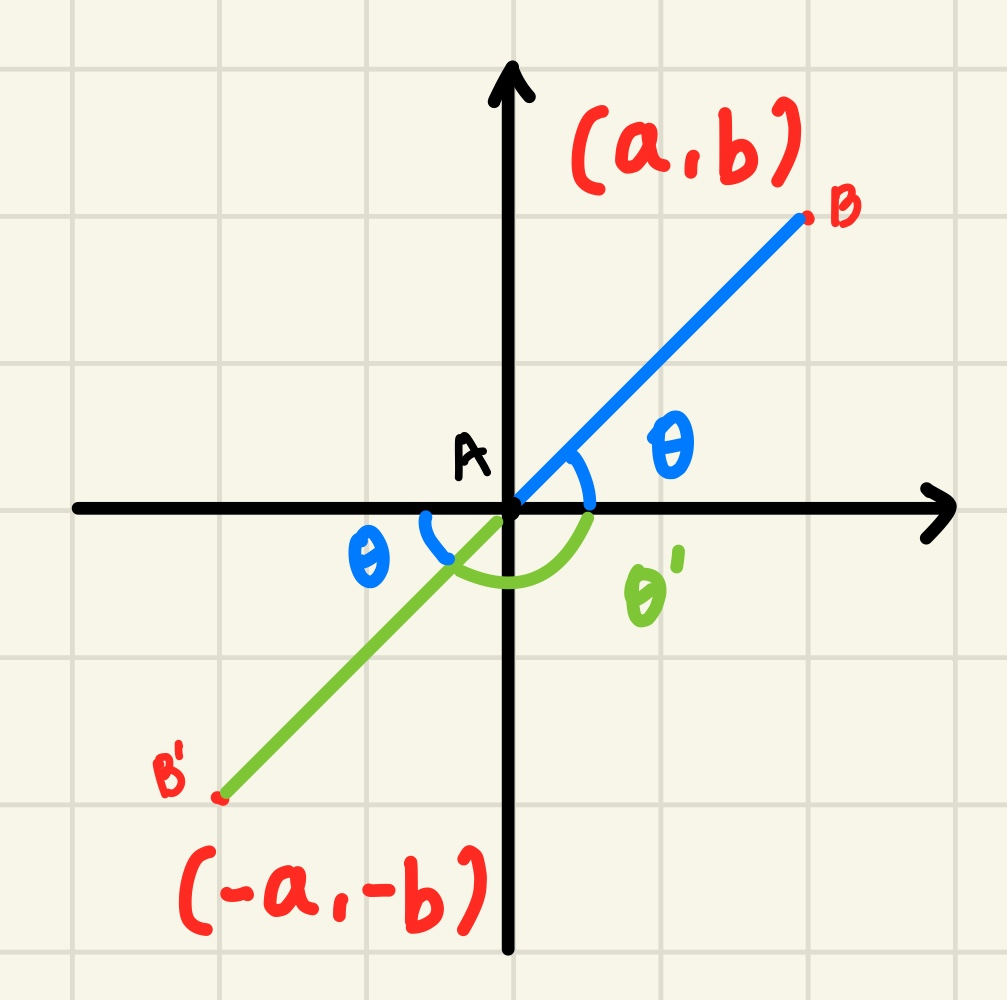
Math.Atan2
가로 세로 비율이 아닌, x 와 y 좌표를 각각 입력하여 라디안을 구한다.
[-π , π] 의 라디안 값으로 반환)
public static float Atan2 (float y, float x);이를 통해, Atan2(b,a) 와 Atan2(-b,-a) 는 각각 θ 와 θ' 를 반환한다.
Atan2 의 장점
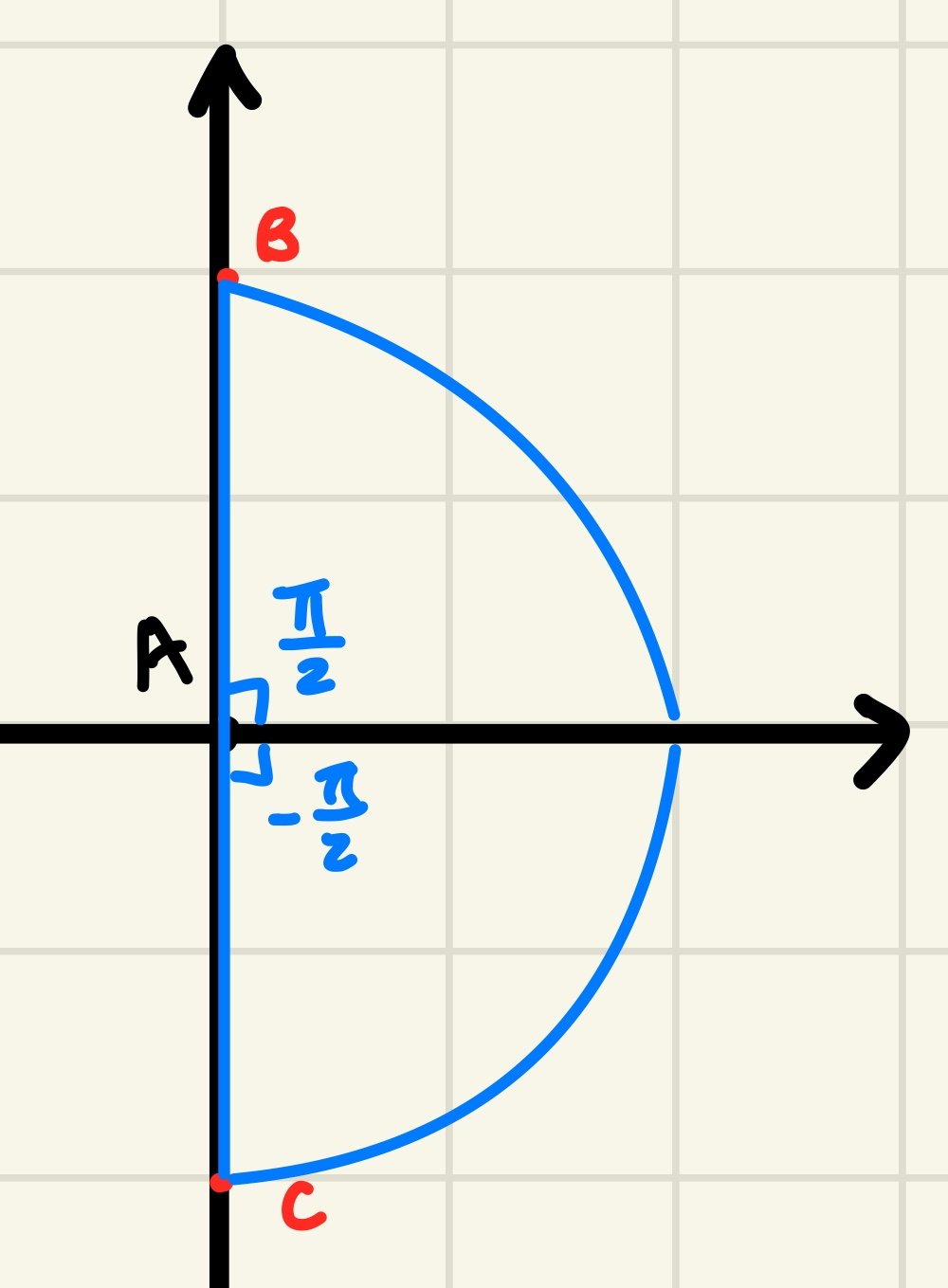다음과 같이 (0,B) 좌표와 (0,C) 좌표의 라디안을 구할 때를 가정해보자.
(B > 0 , C < 0)
float theta1 = Math.Atan(y/x);
float theta2 = Math.Atan2(y,x);Atan(y/x) 의 경우, x 의 값이 0 이면 y / 0 으로 Divide by Zero 에러가 발생할 수 있다.
반면, Atan2(y,x) 의 경우, x 를 따로 입력 받으므로 에러가 발생하지 않는다.
Atan2(B,0) = π/2 , Atan2(C,0) = -π/2 의 값을 얻을 수 있다.
Atan 함수의 활용
- 시야각 기능 : 90도 범위의 시야각을 가질 때
- Atan2 함수를 통해서 -45' ~ 45' 사이에 물체가 있는지 확인
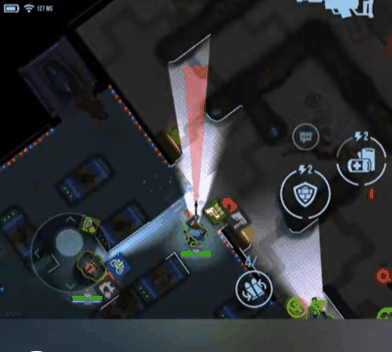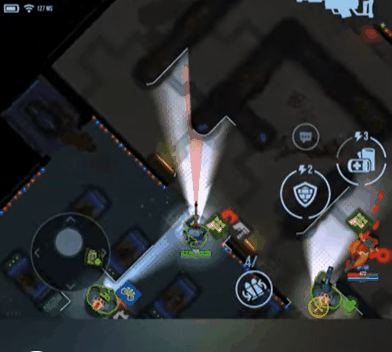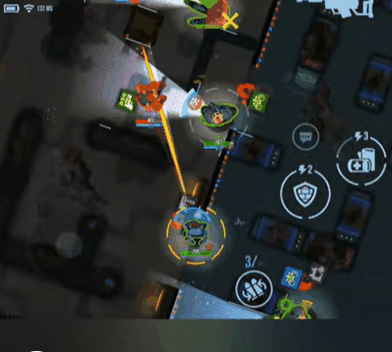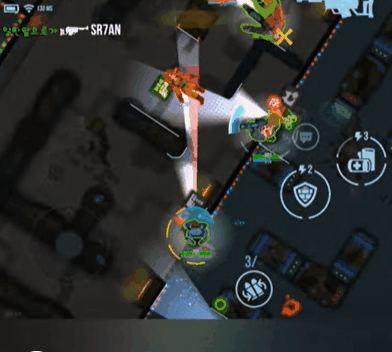
- 투사체 : 자연스럽게 투사체가 퍼지게 할 때
- 오브젝트가 바라보는 방향을 기점으로 -θ , +θ 범위 사이에 투사체를 발사
TIL 마무리
사원수와 오일러 각을 공부하기 위해, 오랜만에 게임 수학 책을 폈다.
필요한 부분만 찾아서 읽다보니, 이해하기 어려워 시간이 오래 걸려 TIL 쓰는 시간이 너무 소요된 것 같다.
부트캠프가 다 끝난 뒤, 게임 수학 책을 정독하며 쿼터니언과 오일러 각 사이의 변환 과정 등을 이해하고 정리 해보고 싶다.
