IEEE Floating Point 정리

수학적 형태

$(-1)^{s}M2^{E}$

Example:
$15123_{10} = (-1)^{0}*1.1101101101101_{2}*2^{13}$

• s: sign bit
• M: 일반적으로 [1.0~2.0) range의 분수 값
  $(1.000..._{2} \sim 1.111..._{2})$
• E: 2의 거듭제곱의 가중치

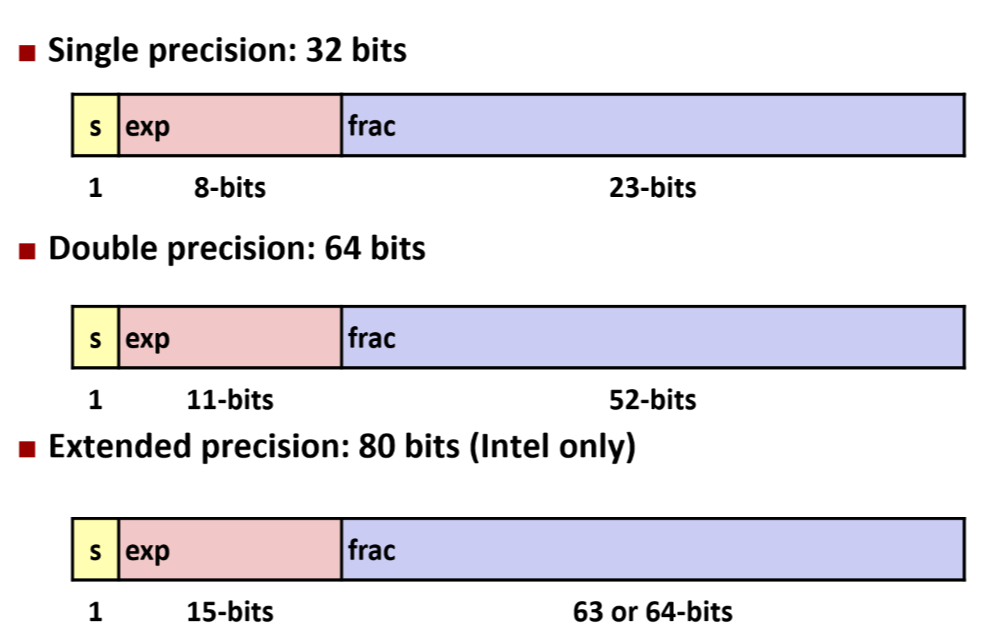
인코딩

• MSB s: sign bit
• exp: E의 인코딩 결과
• frac: M의 인코딩 결과
  

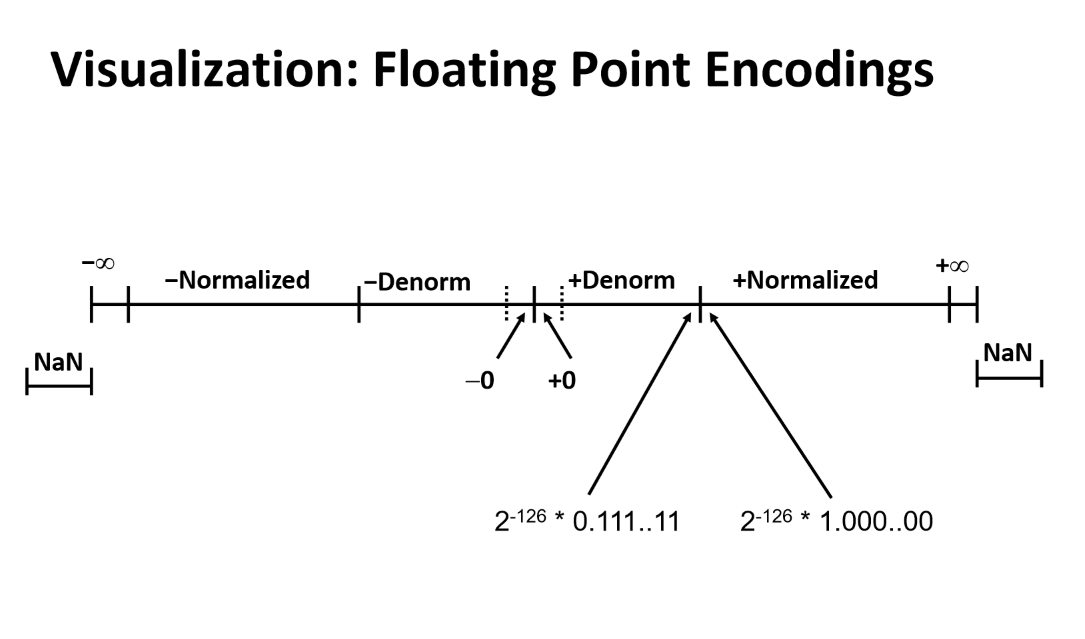
Denormalized, Normalized, Special

IFFF Floating points는 exp의 값에 따라 위 세가지 종류로 나뉨.

Normalized
when exp != 000...0 && exp != 111...1

• $E = exp - Bias$
  $Bias = 2^{k-1}-1 (k는\; exp \;비트\; 수)$
• $M = 1.\mathsf{xx...x}_{2}$
  xx...x: frac field에 들어갈 bit

Example

float f = 15213.0;

$15213_{10} = 11101101101101_{2}=1.1101101101101_{2}*2^{13}$

s = 0

E = 13, bias = 127(in single precision)
exp = E + bias = 13 + 127 = 140 = 10001100

M = 1.1101101101101
frac = 11011011011010000000000

Result: 0 10001100 11011011011010000000000

Denormalized
when exp = 000...0

• $E=1-Bias$
• $M=0.\mathsf{xx...x}_{2}$

case1: exp = 000...0, frac = 000...0
$\rarr$ 0을 표현. +0과 -0이 나타남.
cases2: exp = 000...0, frac != 000...0
$\rarr$ 0에 가까운 수. 매우 작은 소수

Special
when exp = 111...1

case1: exp = 111...1, frac = 000...0
$\rarr$ $\infin$을 표현. overflow임. 음양 모두 가짐.
case2: exp = 111...1, frac != 000...0
$\rarr$ NAN. 표현할 수 있는 수 값이 없음.

---

Rounding

0에서 멀어질 수록 정밀도가 떨어짐

$\rarr$ Rounding(근사) 필요

다양한 근사 모델

• Towards zero: 0에 가까운 방향으로 근사
• Round down: 음의 방향으로 근사
• Round up: 양의 방향으로 근사
• Nearest Even: 가까운 방향으로 근사
  사이 값일 경우 가까운 짝수 방향으로 근사

우리는 Nearest Even 모델을 기본으로 설정함.

왜 이거 씀?
단순 올림이나 내림은 통계적으로 편향을 만들어 평균값이 실제보다 커지게 됨.

방식
가능한 두 값의 중간보다 클 경우 $\rarr$ 큰 값
가능한 두 값의 중간보다 작을 경우 $\rarr$ 작은 값
가능한 두 값의 중간일 경우 $\rarr$ 가까운 짝수

예) 10진수에서
7.8949999 $\rarr$ 7.89 (가능한 두 값의 중간보다 작음)
7.8950001 $\rarr$ 7.90 (가능한 두 값의 중간보다 큼)
7.8950000 $\rarr$ 7.90 (가능한 두 값의 중간, 가까운 짝수는 7.90임)
7.8850000 $\rarr$ 7.88 (가능한 두 값의 중간, 가까운 짝수는 7.88임)

예) 2진수에서
("Even" when lsb is 0
("Half way" when bits to right of rounding position = 100...0)
10.00011 $\rarr$ 10.00 (<1/2)
10.00110 $\rarr$ 10.01 (>1/2)
10.11100 $\rarr$ 11.00 (1/2)
10.10100 $\rarr$ 10.10 (1/2)

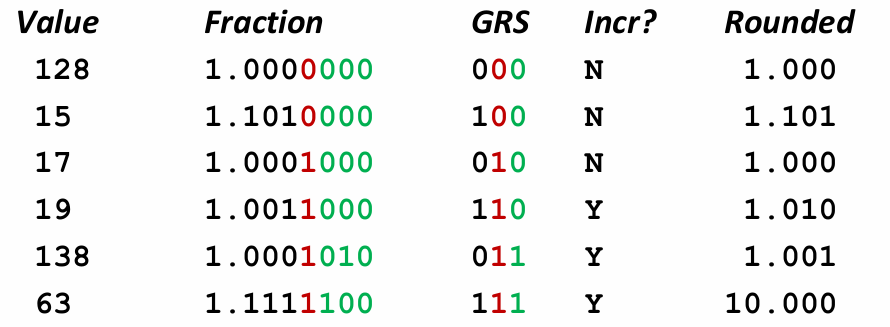
Rounding in floating point
$f = 1.BBGRXXX$

• Guard bit(G): rounding한 결과의 lsb
• Round bit(R): rounding에 의해 버려질 bit의 msb
• Sticky bit(XXX): round bit 뒤의 모든 비트에 OR 연산 결과

Round up되는 경우
Round = 1, Sticky = 1 $\rarr$ 반올림
Guard = 1, Round = 1, Sticky = 0 $\rarr$ 가까운 짝수로

예)

---

연산

FP Multiplication

• $(-1)^{s1}M1*2^{E1} \;*\;(-1)^{s2}M2*2^{E2} = (-1)^sM*2^{E}$
  s = s1^s2
  M = M1 * M2
  E = E1 + E2

*Fixing
M이 2 이상이 되면 우측 시프트 후 E 증가
E가 범위를 벗어나면 overflow
frac precision에 맞게 M 라운딩

예) $1.010*2^{2}\;*\;1.110*2^{3}$
s = 0^0 = 0
M = 1.010 * 1.110 = 10.0011
E = 2 + 3 = 5

shift M right 1:
10.0011 $\rarr$ 1.00011, E = E+1
round M to fit frac:
1.00011 $\rarr$ 1.001

result: $1.001*2^{6}$

FP Addition

• $(-1)^{s1}M1*2^{E1} \;+\;(-1)^{s2}M2*2^{E2} = (-1)^sM*2^{E}$
  $(E1 > E2)$
  s, M = 정렬 후 sign addition 결과
  E = 더 큰 거(E1)

*Fixing
M이 2 이상이 되면 우측 시프트 후 E 증가
M이 1보다 작으면 좌측 시프트 후 E 감소
E가 범위를 벗어나면 overflow
frac precision에 맞게 M 라운딩

예) $1.010*2^{2}\;+\;1.110*2^{3}$
덧셈 연산을 위해 align:
$1.010*2^{2} \rarr 0.1010*2^{3}$
$1.110*2^{3} \rarr 1.1100*2^{3}$
덧셈:
$(0.1010+1.1100)*2^{3} = 10.0110*2^{3}$
shift M right 1:
10.0110 $\rarr$ 1.00110, E = E+1
round M to fit frac:
1.00110 $\rarr$ 1.010

result: $1.010*2^{4}$

---

<참고자료>
Bryant and O’Hallaron, Computer Systems: A Programmer’s Perspective, Third Edition
안성용, "시스템소프트웨어", 부산대학교