Memory 성능의 특성
- 주소를 띄엄띄엄 접근할 수록 (stride가 커질 수록)
-> Spatial locality가 낮아짐 - 접근하는 데이터의 크기가 커질 수록
-> Temporal locality가 낮아짐
성능이 안좋아진다.
행렬곱 Spatial locality 개선 문제
조건
- N×N 행렬, 원소 자료형은 double.
- 캐시 블록 크기는 32B
- 행렬 차원(N)은 매우 커서 캐시가 한번에 여러 개의 행을 담지 못한다
+---+ +---+ +---+
| A | * | B | = | C |
+---+ +---+ +---+1번 코드 (ijk)
/* ijk */
for (i=0; i<n; i++) {
for (j=0; j<n; j++) {
sum = 0.0;
for (k=0; k<n; k++) {
sum += a[i][k] * b[k][j];
}
c[i][j] = sum;
}
}시간 복잡도 : O(N^3)
연산 방식 :
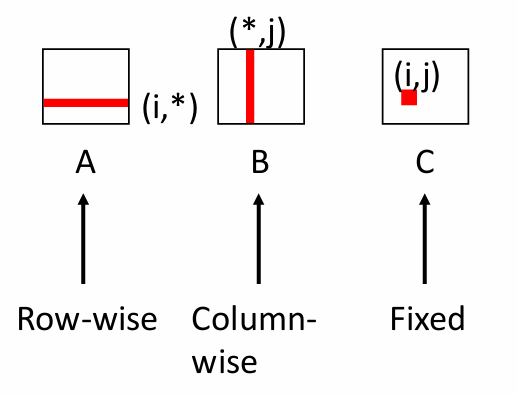
성능 분석 :
행렬 a의 경우 고정된 i(행)에 대해 순차적 접근이 이루어진다(stride-1).
따라서 행의 첫 원소에서만 miss가 나고 이후 원소는 캐시에 올라가 있는 상태가 되므로
miss rate = sizeof(a[i][k]) / Block Size
문제에서 행렬의 원소는 double 자료형이고 블록 크기는 32B이므로
miss rate = 8 / 32 = 1 / 4 = 0.25
행렬 c의 경우 쓰기 연산만 있고, 읽기 miss가 없기 때문에
miss rate = 0.0
문제점
b[k][j]로 원소를 계속 참조하게 되면 b 행렬에서는 매 inner loop마다 행을 건너뛰며 참조하게 됨.
-> No Spatial Locality
매 참조마다 miss가 발생하기 때문에
miss rate = 1.0
따라서
misses/iter = 1.25
2번 코드 (kij)
/* kij */
for (k=0; k<n; k++) {
for (i=0; i<n; i++) {
r = a[i][k];
for (j=0; j<n; j++) {
c[i][j] += r * b[k][j];
}
}
}시간 복잡도 : O(N^3)
연산 방식 :
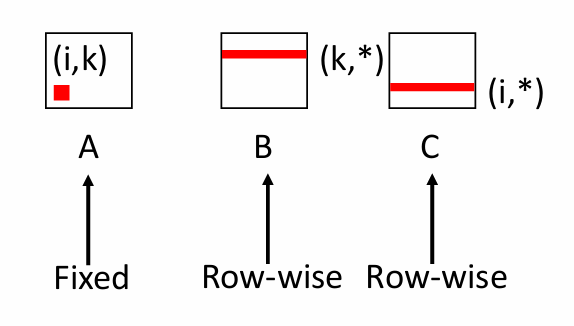
성능 분석 :
행렬 a의 경우 고정된 상태로 inner loop에서 사용되기 때문에
miss rate = 0.0
행렬 b는 고정된 k(행)에 대해 순차적 접근이 이루어진다.
miss rate = 0.25
행렬 c도 마찬가지로 고정된 i(행)에 대해 순차적 접근이 이루어진다.
miss rate = 0.25
따라서
misses/iter = 0.5
-> Best case
행렬곱 Temporal locality 개선 문제
위 문제를 통해 Spatial locality 최적화를 배웠다.
이번에는 Temporal locality 최적화까지 진행해보자.
조건
- N×N 행렬, 원소 자료형은 double.
- Cache block = 8 doubles (= 64B)
- Cache size C << n (n 보다 훨씬 작다)
1번 코드 (not blocked)
c = (double*) calloc(sizeof(double), n*n);
void mmm(double* a, double* b, double* c, int n) {
int i, j, k;
for (i=0; i<n; i++) {
for (j=0; j<n; j++) {
for (k=0; k<n; k++) {
c[i*n + j] += a[i*n + k] * b[k*n + j];
}
}
}
}시간 복잡도 : O(N^3)
연산 방식 :
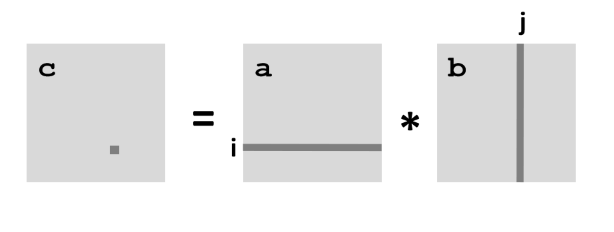
성능 분석 :
-
1st iter
a는 stride-1 참조가 이루어지고 있다.
행 하나 당 데이터 개수가 n개 이므로 캐시에는8개 씩 로드 되고 총n/8번의 로드가 필요하다.
한 번 로드될 때 마다 miss가 한 번씩 발생하므로
miss_in_a = n/8
b는 행을 건너뛰며 참조가 이루어지므로 매 참조마다 miss가 발생한다.
miss_in_b = n
따라서
total_miss_iter1 = n/8 + n = 9n/8
그리고 마지막에 읽은 블록들이 캐시에 남는다. -
2nd iter
miss 횟수는 1st iter와 같다.
total_miss_iter2 = 9n/8
i가 n번 j가 n번 총 n*n번 반복될 것이기 때문에
total_misses = 9n/8 * n * n = (9/8)*n^3
2번 코드 (Blocked Matrix Multiplication)
조건 추가
- 세개의 블록이 캐시에 들어갈 수 있다 : 3B*B < C
c = (double*) calloc(sizeof(double), n*n);
void mmm(double* a, double* b, double* c, int n) {
int i, j, k;
for (i=0; i<n; i+=B)
for (j=0; j<n; j+=B)
for (k=0; k<n; k+=B)
for (i1=i; i1<i+B; i1++)
for (j1=j; j1<j+B; j1++)
for (k1=k; k1<k+B; k1++)
c[i1*n+j1] += a[i1*n+k1]*b[k1*n+j1];성능 분석 :
한 번의 블록 곱셈에 사용되는 블록 개수
a_block : B×B
b_block : B×B
c_block : B×B
처음 블록에 접근할 때만 cold miss가 발생하고 이후 블록 연산 중에 miss는 발생하지 않는다.
(연산에 필요한 모든 데이터가 캐시에 들어가기 때문)
하나의 블록은 B^2개의 double을 가지므로 블록 하나 당 미스 발생 횟수는 B^2/8.
a와 b 각각 블록이 순회하는 행 또는 열에 대하여 n/B개 있으므로 블록 개수는 2n/B개.
1회 순회에 miss 발생 횟수는
miss_per_iter = 2n/B * B^2/8 = nB/4
총 iter 횟수는 n/B^2회이므로
total misses = nB/4 * (n/B)^2 = n^3/4B
핵심 정리
Spatial Locality 최적화
- 문제상황 :
stride-n 접근을 하는 inner loop 때문에 miss rate가 높아짐- 해결방법 :
열이 아닌 행 기준 접근이 되도록 loop 순서 조정
->loop rearangingTemporal Locality 최적화
- 문제상황 :
loop에서 자주 접근하는 데이터들이 캐시에 다 담기지 않아서 잦은 load 발생- 해결방법 :
데이터를 캐시 크기에 맞는 블록으로 쪼개서 계산, cache reuse 극대화.
->Blocking 기법
여담 : 두 기법을 모두 적용한 행렬곱
#include <stdlib.h>
void blocked_mmm(double* a, double* b, double* c, int n, int B) {
int i, j, k, i1, j1, k1;
for (i = 0; i < n; i += B)
for (k = 0; k < n; k += B)
for (j = 0; j < n; j += B)
for (i1 = i; i1 < i + B && i1 < n; i1++)
for (k1 = k; k1 < k + B && k1 < n; k1++)
double r = a[i1 * n + k1];
for (j1 = j; j1 < j + B && j1 < n; j1++)
c[i1 * n + j1] += r * b[k1 * n + j1];
}
<참고자료>
Bryant and O’Hallaron, Computer Systems: A Programmer’s Perspective, Third Edition
안성용, "시스템소프트웨어", 부산대학교
