LSTM 개념

이 글을 읽기 전, RNN을 먼저 공부하는 걸 추천합니다.

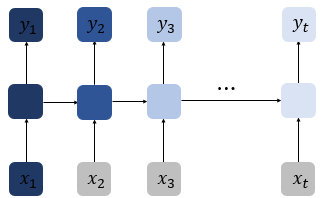
앞서 공부한 RNN에서는 time step이 길어질 수록 앞의 정보가 뒤로 충분히 전달되지 못하는 현상이 발생하는데, 아래의 그림처럼 첫번 째 입력값인 $x_1$ 의 정보량을 색으로 표현하였고, time step이 흐를 수록 색이 얕아지는 것은 정보량이 손실되어가는 과정을 표현한 그림이다. 뒤로 갈수록 $x_1$의 정보량은 손실되고, long sequence의 경우에는 $x_1$의 전체 정보에 대한 영향력은 의미가 미미해진다. 이를 장기 의존성 문제(problem of Long-Term Dependencies)라고 한다.

LSTM architecture

RNN의 장기 의존성 문제를 해결하기 위해 만들어진 장단기 메모리(Long Short-Term Memory)이다. LSTM은 hidden layer의 메모리 셀에 입력 게이트, 망각 게이트, 출력 게이트를 추가하여 불필요한 기억을 지우고, 기억해야할 것들을 정한다.

요약하면 LSTM은 은닉 상태(hidden state)를 계산하는 식이 기존의 RNN보다 조금 더 복잡해졌으며 셀 상태(cell state)라는 값이 추가되었다. LSTM은 RNN과 비교하여 long sequence의 입력을 처리하는데 탁월한 성능을 보인다.

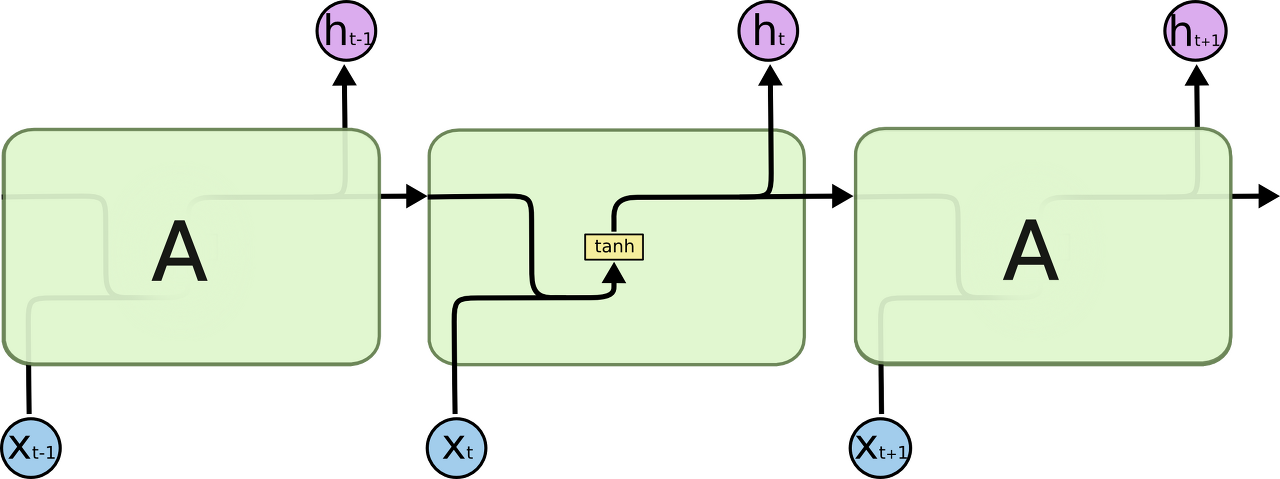
LSTM도 RNN과 마찬가지로 체인 구조를 가지고 있지만, 각 반복 모듈은 다른 구조를 갖고있다. RNN의 반복모듈이 tanh layer 한층 사용 대신 4개의 layer가 특정 방식으로 서로 정보를 주고 받도록 설계되어있다.

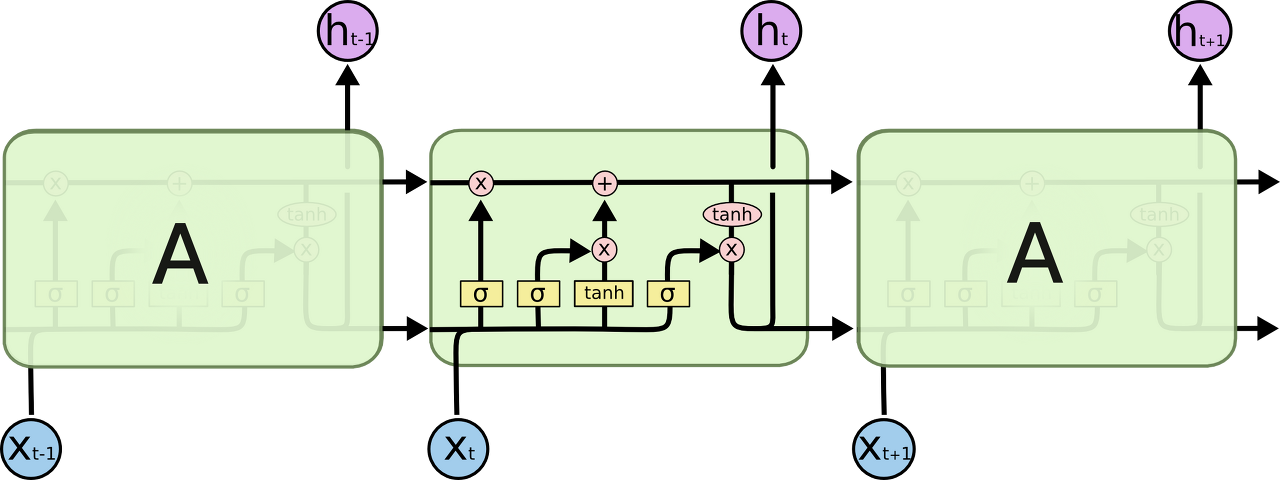
이 글을 읽어나가기 위해 용어에 대한 약속이 필요하다.

위 그림에서 각 선(line)은 한 노드의 output을 다른 노드의 input으로 vector 전체를 보내는 흐름을 나타낸다. 분홍색 동그라미는 vector 합과 같은 pointwise operation을 나타낸다. 노란색 박스는 학습된 neural network layer다. 합쳐지는 선은 concatenation을 의미하고, 갈라지는 선은 정보를 복사해서 다른 쪽으로 보내는 fork를 의미한다.

LSTM의 main idea

LSTM의 핵심은 cell state인데, 모듈 그림에서 수평으로 그어진 윗 선에 해당한다.

cell state : 모듈 그림에서 수평으로 그어진 윗 선에 해당, 컨베이어 밸트처럼 작은 linear interaction만을 적용시키면서 전체 체인을 계속 구동시킨다. 셀 상태 또한 이전에 배운 은닉 상태처럼 이전 시점의 Cell state가 다음 시점의 Cell state를 구하기 위한 입력으로서 사용된다. LSTM은 cell state에 뭔가를 더하거나 없앨 수 있는 능력이 있는데, 이 능력은 gate라고 불리는 구조에 의해서 조심스럽게 제어된다.

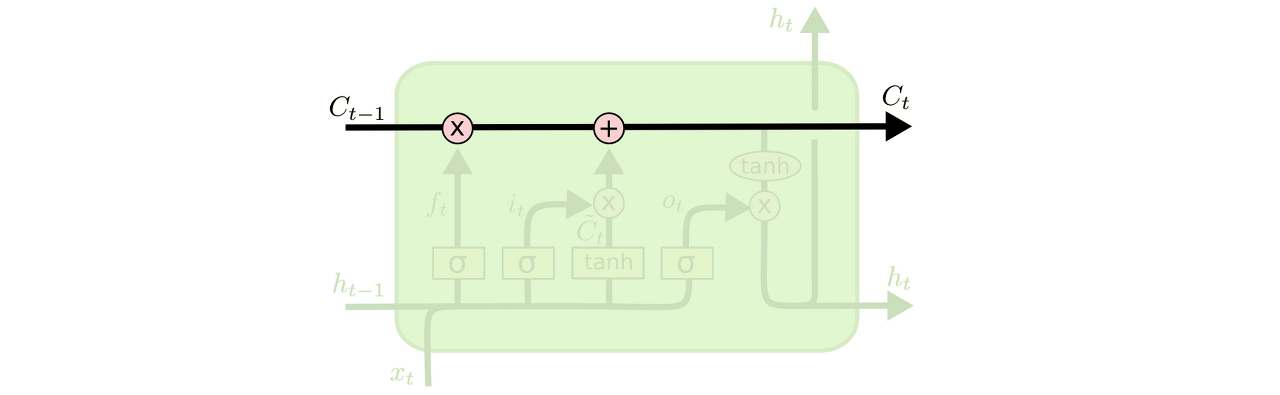
Gate:
정보가 전달될 수 있는 추가적인 방법으로, 모두 Sigmoid layer, pointwise 곱셈으로 이루어져있다.
signmoid layer는 0과 1 사이의 숫자를 내보내는데, 이 값은 각 컴포넌트가 얼마나 정보를 전달해야 하는지에 대한 척도를 나타낸다. 그 값이 0이라면 "아무 것도 넘기지 말라"가 되고, 값이 1이라면 "모든 것을 넘겨라"가 된다.
LSTM은 3개의 gate를 가지고 있고, 이 문들은 cell state를 보호하고 제어한다.

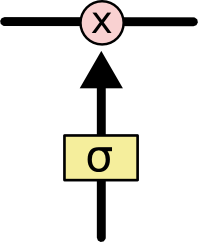
LSTM의 Progress

1. cell state로부터 어떤 정보를 버릴 것인지를 정한다.

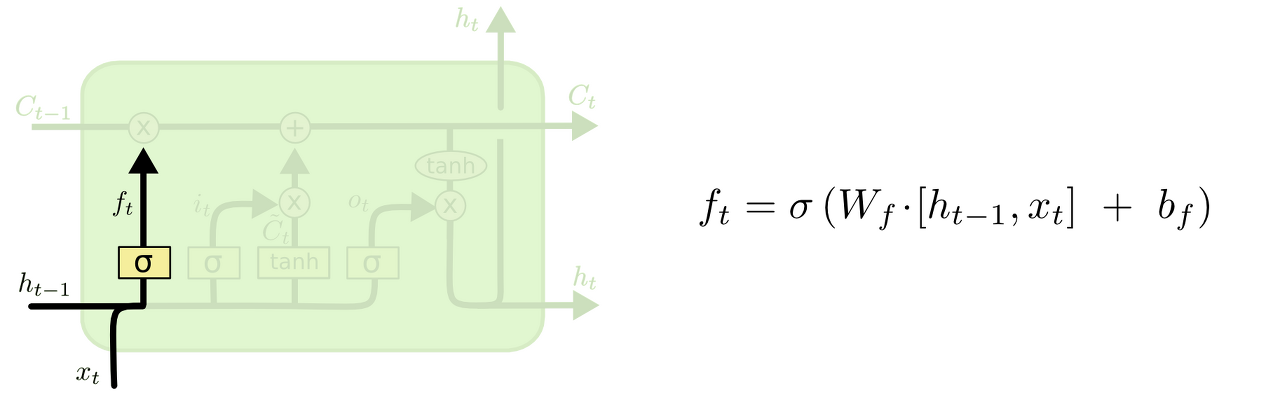
이 gate를 "forget gate layer"라고 부르고, sigmoid layer에 의해 결정된다. 이 단계에서는 $h_{t-1}$ (RNN Cell의 state input)과 $x_t$(input)를 받아서 0과 1 사이의 값을 $C_{t-1}$에 보내준다. sigmoid 함수를 지나면 0과 1 사이의 값이 나오게 되는데, 이 값이 곧 삭제 과정을 거친 정보의 양이다. 0에 가까울수록 정보가 많이 삭제된 것이고 1에 가까울수록 정보를 온전히 기억한 것.

이전 단어들을 바탕으로 다음 단어를 예측하는 언어 모델 예시를 들자면
ex) 여기서 cell state는 현재 주어의 성별 정보를 가지고 있을 수도 있어서 그 성별에 맞는 대명사가 사용되도록 준비하고 있을 수도 있을 것이다. 그런데 새로운 주어가 왔을 때, 우리는 기존 주어의 성별 정보를 생각하고 싶지 않을 것이다.

2. 앞으로 들어오는 새로운 정보 중 어떤 것을 cell state에 저장할 것인지를 정한다.

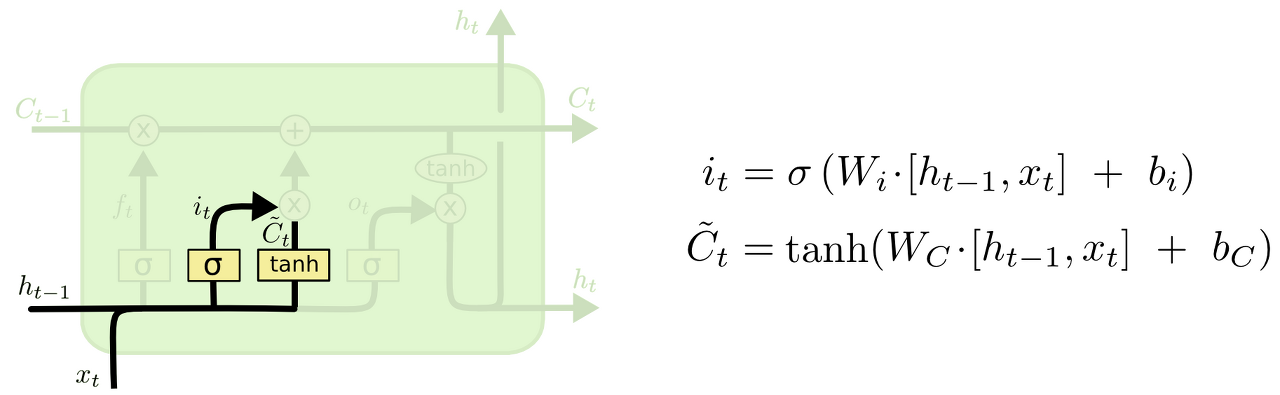
먼저, "input gate layer"라고 불리는 sigmoid layer가 어떤 값을 업데이트할 지 정한다. 그 다음에 tanh layer가 새로운 후보 값들인 $C_t$라는 vector를 만들고, cell state에 더할 준비를 한다. 이렇게 두 단계에서 나온 정보를 합쳐서 state를 업데이트할 재료를 만들게 된다.

ex) 기존 주어의 성별을 잊어버리기로 했고, 그 대신 새로운 주어의 성별 정보를 cell state에 더하고 싶을 것이다.

3. 이제 과거 state인 Ct−1를 업데이트해서 새로운 cell state인 Ct를 만든다.

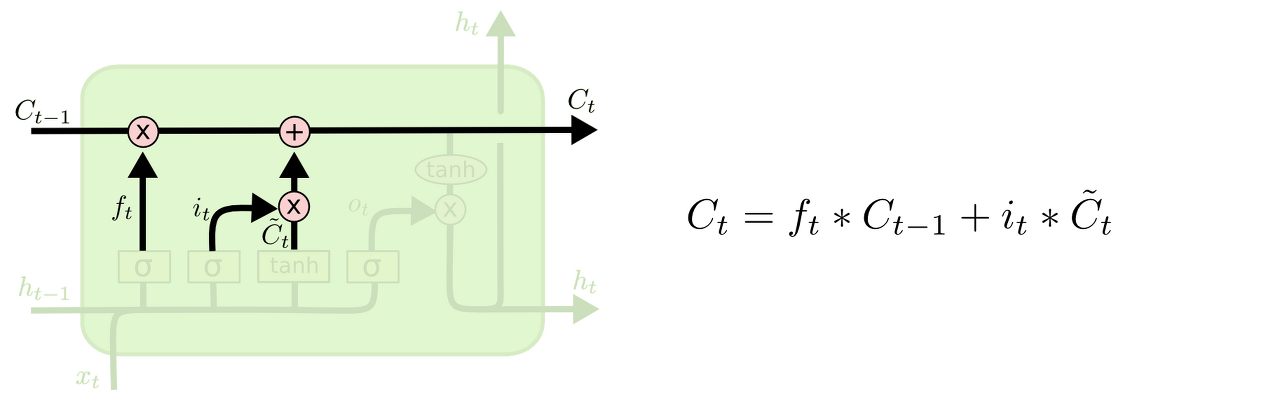
이미 이전 단계에서 어떤 값을 얼마나 업데이트해야 할 지 다 정해놨으므로 여기서는 그 일을 실천만 하면 된다.
우선 이전 Cell state에 ft를 곱해서 가장 첫 단계에서 잊어버리기로 정했던 것들을 진짜로 잊어버린다. 그리고 it ∗ Ct를 더한다. 이 더하는 값은 두 번째 단계에서 업데이트하기로 한 값을 얼마나 업데이트할 지 정한 만큼 scale한 값이 된다.

ex) 이 단계에서 실제로 이전 주어의 성별 정보를 없애고 새로운 정보를 더하게 되는데, 이는 지난 단계들에서 다 정했던 것들을 실천만 하는 단계임을 다시 확인할 수 있다.

4. 무엇을 output으로 내보낼 지 정한다.

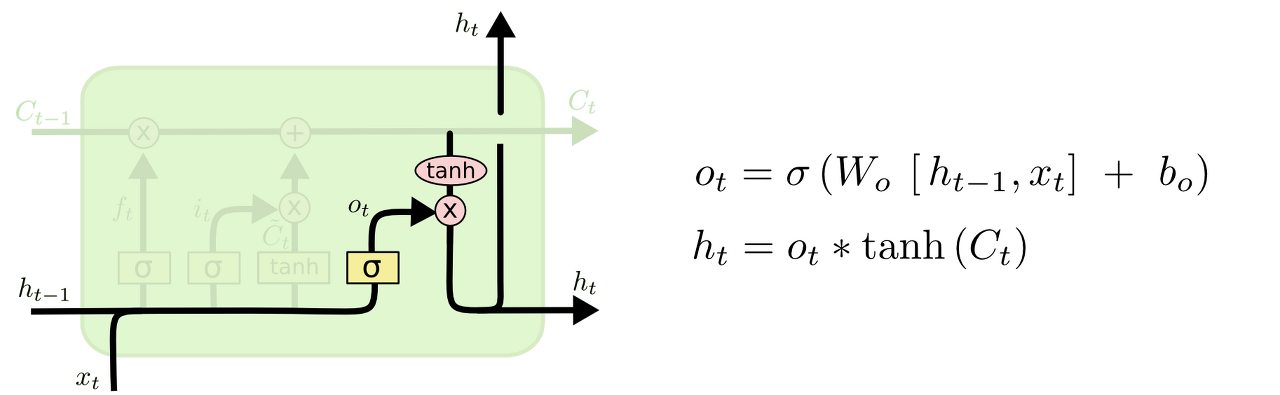
이 output은 cell state를 바탕으로 필터된 값이 될 것이다. 가장 먼저, sigmoid layer에 input 데이터를 태워서 cell state의 어느 부분을 output으로 내보낼 지를 정한다. 그리고나서 cell state를 tanh layer에 태워서 -1과 1 사이의 값을 받은 뒤에 방금 전에 계산한 sigmoid gate의 output과 곱해준다. 그렇게 하면 우리가 output으로 보내고자 하는 부분만 내보낼 수 있게 된다.

ex) 우리는 주어를 input으로 받았으므로 주어 다음에 오게 될 예측값인 output으로 적절한 답은 아마도 동사 개념의 무언가가 될 것이다. 예를 들어 최종적인 Output은 앞에서 본 주어가 단수형인지 복수형인지에 따라 그 형태가 달라질 수도 있는 것이다.

참고하면 좋은 영상 : https://www.youtube.com/watch?v=bX6GLbpw-A4

참고 : https://colah.github.io/posts/2015-08-Understanding-LSTMs/
https://dgkim5360.tistory.com/entry/understanding-long-short-term-memory-lstm-kr
https://smj990203.tistory.com/entry/RNN-LSTM