🔍 Graph
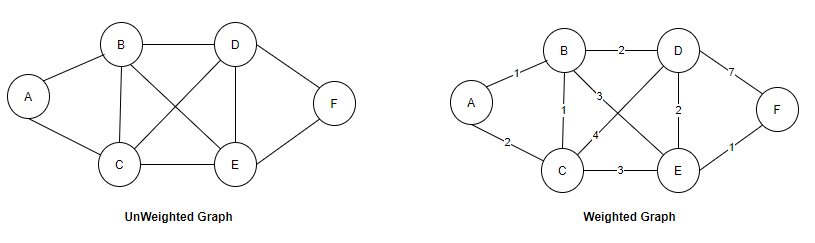
네트워크망과 같이 마치 거미줄 처럼 여러개의 점들이 선으로 복잡하게 연결되어 있는 관계를 표현한 자료구조이다.
직접적인 관계가 있을 경우, 두 점 사이를 이어주는 선이 있으며, 간접적인 관계라면 몇 개의 점과 선에 걸쳐 이어진다.
또한, 하나의 점을 정점(vertex)으로, 하나의 선을 간선(edge)이라고 한다.
- 이미지의 오른 쪽과 같이 간선에 연결의 강도가 적혀 있는 경우 가중치 그래프라고 하며, 왼쪽과 같이 적혀 있지 않은 경우 비가중치 그래프라고 한다.
🔍 Graph의 표현 방식
👀인접 행렬(Adjacency Matrix)
두 정점을 바로 이어주는 간선이 있을 때, 두 정점은 인접하다고 한다.
인접 행렬은 서로 다른 정점들이 인정한 상태인지를 표시한 2차원 배열의 형태를 가진 행렬로, 정점이 이어져 있을 때 1(true), 이어져 있지 않을 때 0(false)로 표시된다.
두 정점간 관계 유무를 바로 확인할 수 있기 때문에 가장 빠른 경로를 찾을 때 주로 사용된다.
단, 연결 가능한 모든 경우의 수를 저장하기 때문에 인접 리스트에 비해 상대적으로 메모리를 많이 차지한다.
무방향 그래프(Undirected Graph)
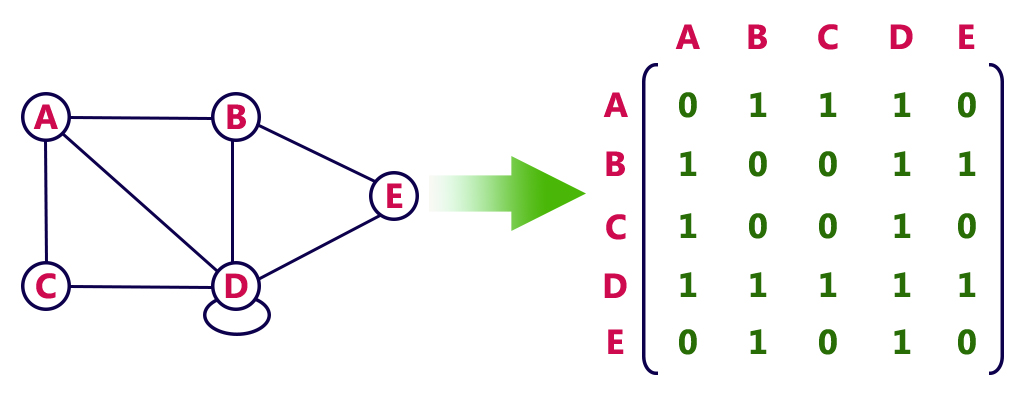
ex) A의 차수 3개: A->B, A->C, A->D
[0][1] === 1
[0][2] === 1
[0][3] === 1
...방향 그래프(directed Graph)
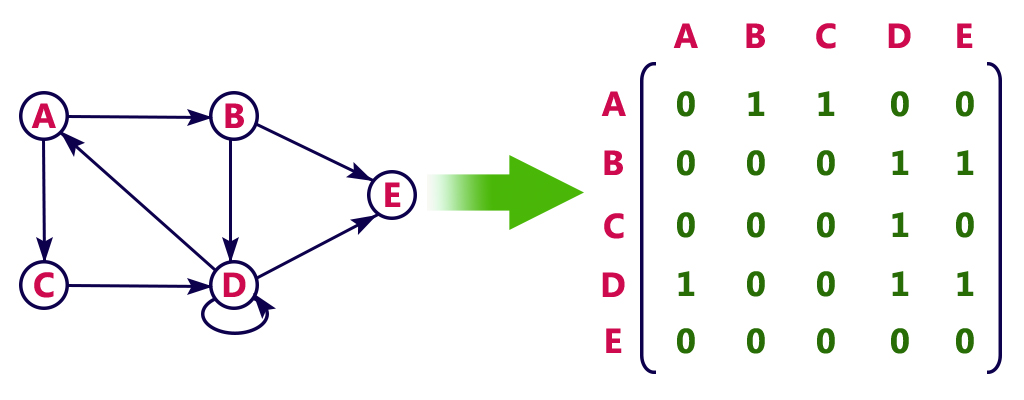
예시는 단방향 그래프이다.
D의 경우, 진출하는 간선이 자기자신에게 진입하기 때문에 자기 루프(Self Loop)를 가졌다고 표현한다.
ex) A의 진출 차수 2개: A->B, A->C
[0][1] === 1
[0][2] === 1
...- 진출 차수: 한 정점에서 나가는 간선의 수
- 진입 차수: 한 정점에 들어오는 간선의 수
✔구현 코드
// directed graph (방향 그래프)
// unweighted (비가중치)
// adjacency matrix (인접 행렬)
// 기존 배열의 인덱스를 정점으로 사용 (0, 1, 2, ... --> 정점)
class GraphWithAdjacencyMatrix {
// graph의 constructor
constructor() {
this.matrix = [];
}
// vertex 추가
addVertex() {
const currentLength = this.matrix.length;
for (let i = 0; i < currentLength; i++) {
this.matrix[i].push(0);
}
this.matrix.push(new Array(currentLength + 1).fill(0));
}
// vertex 탐색
// this.matrix에 vertex가 존재한다면 true를 리턴하고, 반대의 경우라면 false를 리턴.
contains(vertex) {
return !!this.matrix[vertex];
}
// vertex와 vertex를 이어주는 edge 추가
addEdge(from, to) {
const currentLength = this.matrix.length-1;
// 두 가지 인자 중, 어느 하나라도 undefined라면, return
if (from === undefined || to === undefined) {
console.log("2개의 인자가 있어야 합니다.");
return;
}
//TODO: 간선을 추가할 수 없는 상황에서는 추가하지 말아야 합니다.
// from vertex와 to vertex가 전체 그래프의 범위를 벗어난다면, return
if (from > currentLength || to > currentLength || from < 0 || to < 0) {
console.log("범위가 매트릭스 밖에 있습니다.");
return;
}
//TODO: 간선을 추가해야 합니다.
// this.matrix[from][to]의 값을 1로 바꿔줘서 edge로 연결이 되어 있음을 표시
this.matrix[from][to] = 1;
}
// from vertex와 to vertex 사이에 edge를 가지고 있는지 여부를 판단
hasEdge(from, to) {
return !!this.matrix[from][to];
}
// from vertex와 to vertex 사이에 관련이 없다면, edge를 제거
removeEdge(from, to) {
const currentLength = this.matrix.length-1;
// 두 가지 인자 중, 어느 하나라도 undefined라면, return
if (from === undefined || to === undefined) {
console.log("2개의 인자가 있어야 합니다.");
return;
}
// from vertex와 to vertex가 전체 그래프의 범위를 벗어난다면, return
if (from > currentLength || to > currentLength || from < 0 || to < 0) {
console.log("범위가 매트릭스 밖에 있습니다.");
return;
}
// this.matrix[from][to]의 값을 1로 바꿔줘서 edge로 연결이 되어 있음을 표시
this.matrix[from][to] = 0;
}
}
// 입출력(사용 예시)
const adjMatrix = new GraphWithAdjacencyMatrix();
adjMatrix.addVertex();
adjMatrix.addVertex();
adjMatrix.addVertex();
console.log(adjMatrix.matrix);
/*
TO
0 1 2
0 [0, 0, 0],
FROM 1 [0, 0, 0],
2 [0, 0, 0]
*/
let zeroExists = adjMatrix.contains(0);
console.log(zeroExists); // true
let oneExists = adjMatrix.contains(1);
console.log(oneExists); // true
let twoExists = adjMatrix.contains(2);
console.log(twoExists); // true
adjMatrix.addEdge(0, 1);
adjMatrix.addEdge(0, 2);
adjMatrix.addEdge(1, 2);
let zeroToOneEdgeExists = adjMatrix.hasEdge(0, 1);
console.log(zeroToOneEdgeExists); // true
let zeroToTwoEdgeExists = adjMatrix.hasEdge(0, 2);
console.log(zeroToTwoEdgeExists); // true
let oneToZeroEdgeExists = adjMatrix.hasEdge(1, 0);
console.log(oneToZeroEdgeExists); // false
console.log(adjMatrix.matrix);
/*
TO
0 1 2
0 [0, 1, 1],
FROM 1 [0, 0, 1],
2 [0, 0, 0]
*/
adjMatrix.removeEdge(1, 2);
adjMatrix.removeEdge(0, 2);
let oneToTwoEdgeExists = adjMatrix.hasEdge(1, 2);
console.log(oneToTwoEdgeExists); // false
zeroToTwoEdgeExists = adjMatrix.hasEdge(0, 2);
console.log(zeroToTwoEdgeExists); // false
console.log(adjMatrix.matrix);
/*
TO
0 1 2
0 [0, 1, 0],
FROM 1 [0, 0, 0],
2 [0, 0, 0]
*/👀인접 리스트(Adjacency List)
각 정점이 어떤 정점과 인접하는 지를 리스트의 형태로 표현한다.
각 정점마다 하나의 리스트를 가지며, 자신과 인접한 다른 정점을 담는다.
메모리를 많이 차지하는 인접행렬를 대체함으로써, 메모리를 효율적으로 사용하고 싶을 때 사용한다.
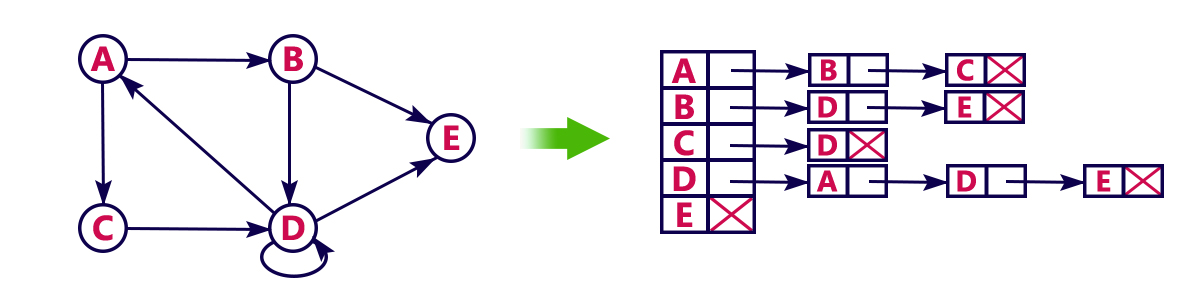
인접하는 정점이 두 개 이상일 경우, 리스트에 담을 때 순서는 중요하지 않다.(단순 나열)
단, 우선 순위를 고려해 구현하여 정렬할 수는 있다.
그러나 만약, 우선 순위를 다뤄야하는 경우라면 인접리스트가 아니라 queue, heap를 사용하는 것이 합리적이다.
✔구현 코드
// undirected graph (무향 그래프)
// adjacency list (인접 리스트)
class GraphWithAdjacencyList {
constructor() {
this.vertices = {};
}
// vertex 추가
addVertex(vertex) {
// 넘겨받은 인자(정점)=> key, 빈 배열 => value
// 이미 존재하는 정점이라면, 덮어 씌워지지 않아야 함.
this.vertices[vertex] = this.vertices[vertex] || [];
}
// 인자로 넘겨받은 정점의 존재여부 return.
contains(vertex) {
return !!this.vertices[vertex];
}
// edge 추가
addEdge(fromVertex, toVertex) {
// 넘겨받은 2개의 정점 모두 존재하는 정점이어야 함. -> 하나라도 없으면 아무것도 하지않고 종료
if (!this.contains(fromVertex) || !this.contains(toVertex)) {
return;
}
// edge가 없을 경우, fromVertex의 인접 리스트에 toVertex 추가
if (!this.hasEdge(fromVertex, toVertex)) {
this.vertices[fromVertex].push(toVertex);
}
// edge가 없을 경우, toVertex의 인접 리스트에 fromVertex 추가
if (!this.hasEdge(toVertex, fromVertex)) {
this.vertices[toVertex].push(fromVertex);
}
}
// edge 존재 여부 판별
hasEdge(fromVertex, toVertex) {
// 만약 정점(fromVertex)이 존재하지 않는다면 false return
if (!this.contains(fromVertex)) {
return false;
}
// 존재한다면 해당 정점의 리스트에 toVertex가 포함되어있는지 return
return !!this.vertices[fromVertex].includes(toVertex);
}
// edge 삭제
removeEdge(fromVertex, toVertex) {
// 인자로 넘겨받은 두 정점이 하나라도 존재하지 않으면, 아무것도 하지않고 종료
if (!this.contains(fromVertex) || !this.contains(toVertex)) {
return;
}
// 인자로 넘겨받은 두 정점이 모두 존재한다면
// TODO: 첫번째 정점의 인접 리스트에 두번째 정점이 있을 경우
// fromVertex의 인접 리스트에 있는 toVertex를 삭제
if (this.hasEdge(fromVertex, toVertex)) {
// 두번째 정점(toVertex)의 인덱스를 찾은 뒤 삭제
const index = this.vertices[fromVertex].indexOf(toVertex);
this.vertices[fromVertex].splice(index, 1);
}
// TODO: 두번째 정점의 인접 리스트에 첫번째 정점이 있을 경우
// toVertex의 인접 리스트에 있는 fromVertex를 삭제
if (this.hasEdge(toVertex, fromVertex)) {
// 첫번째 정점(fromVertex)의 인덱스를 찾은 뒤 삭제
const fromVertexIndex = this.vertices[toVertex].indexOf(fromVertex);
this.vertices[toVertex].splice(fromVertexIndex, 1);
}
}
// vertex 삭제
removeVertex(vertex) {
// 인자로 넘겨받은 정점(A)이 존재한다면
if (this.contains(vertex)) {
// 해당 정점(A)과 연결된 간선을 지우고
while (this.vertices[vertex].length > 0) {
this.removeEdge(this.vertices[vertex][0], vertex);
}
// 최종적으로 해당 정점(A)을 삭제
delete this.vertices[vertex];
}
}
}
// 입출력(사용 예시)
const adjList = new GraphWithAdjacencyList();
adjList.addVertex("Seoul");
adjList.addVertex("Daejeon");
adjList.addVertex("Busan");
adjList.contains("Seoul"); // true
adjList.contains("Jeonju"); // false
adjList.addEdge("Daejeon", "Seoul");
adjList.hasEdge("Seoul", "Daejeon"); //true
adjList.removeVertex("Seoul");
adjList.hasEdge("Seoul", "Daejeon"); //false
...🔥 실사용 예시
✔ 네비게이션(길 찾기)
- 정점: 서울, 대전, 부산
- 간선: 서울-대전, 대전-부산, 부산-서울
위와 같은 조건일 때, 간단한 javascript 객체를 이용해 비유하면 아래와 같다.(비가중치 그래프)
let isConnected = {
seoul: {
busan: true,
daejeon: true
},
daejeon: {
seoul: true,
busan: true
},
busan: {
seoul: true,
daejeon: true
}
}
console.log(isConnected.seoul.daejeon) // true
console.log(isConnected.daejeon.busan) // trueReference:
