분할 정복

분할 정복

• 큰 문제를 작은 부분 문제로 나누어 해결하는 방법(ex.합병정렬, 퀵정렬, 이진검색)
• 분할 정복 과정
  • 문제를 하나 이상의 작은 부분들로 분할
  • 부분들을 각각 정복
  • 부분들의 해답을 통합하여 원래 문제의 답을 구함
• 분할 정복 장점
  • 문제를 나누어 처리하며 어려운 문제 해결 가능
  • 병렬처리에 이점이 있음
• 분할 정복 단점
  • 메모리를 많이 사용(재귀 호출 구조)

예시

• 최댓값 찾기
  
  

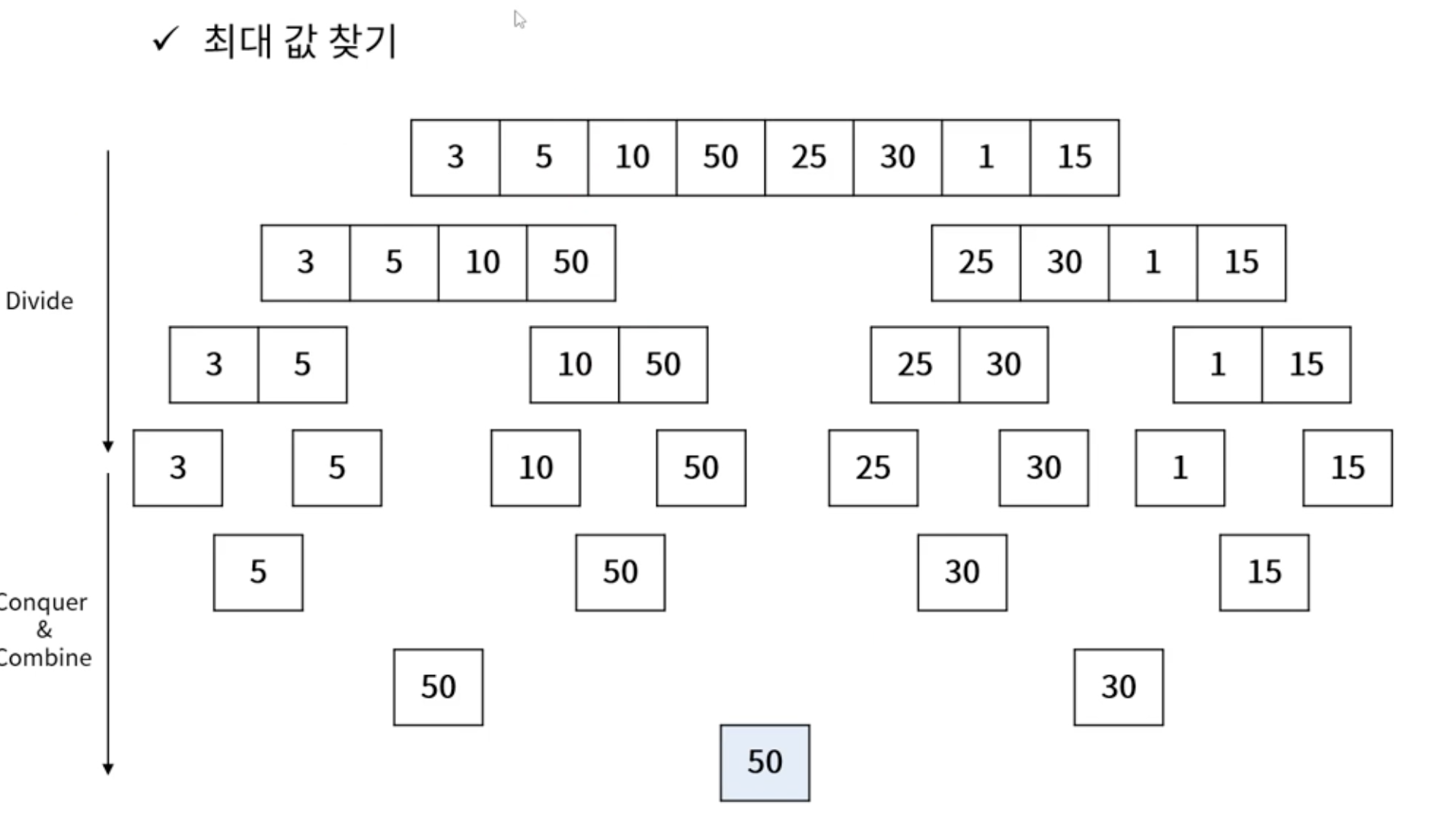
문제

// 정수열 배열 nums에서 연속된 부분 배열의 합 중 가장 큰 값을 출력
// 입력 예시 nums : -5, 0, -3, 4, -1, 3, 1, -5, 8
// 출력 : 10

    public static int solution(int[] nums){
        if(nums==null || nums.length == 0){
            return 0;
        }

        return divideSubArray(nums, 0, nums.length-1);
    }
    
    public static int diviedSubArray(int[] nums, int left, int right){
    	if(left == rught){
        	return nums[left];
        }

        int mid = left + (right - left) / 2;
        int maxLeft = diviedSubArray(nums, left, mid);
        int maxRight = diviedSubArray(nums, mid+1, right);

       	int maxArr = getMaxSubArray(nums, left, mid, right);

        return Math.max(maxLeft, Math.max(maxRight, maxArr));
    }

    public static int getMaxSubArray(int[] nums, int left, int mid, int right){
    	int sumLeft = 0;
        int maxLeft = Integer.MIN_VALUE;

        for(int i=mid; i>=left; i--){
        	sumLeft += nums[i];
            maxLeft = Math.max(maxLeft, sumLeft);
        }

        int sumRight = 0;
        int maxRight = Integer.MIN_VALUE;
        for(int i=mid+1; i<=right; i++){
        	sumRight += nums[i];
            maxRight = Math.max(maxRight, sumRight);
        }

        return maxLeft + maxRight;
    }