(C++) Programmers: 순위

문제

문제 링크

풀이

다음의 문제는 그래프 문제로 저는 DFS를 사용했습니다!
먼저 입출력 예를 그림으로 그려봤습니다.

5번을 2번이 이기고, 2번을 1,3,4번이 이기며 3번을 4번이 이긴 것을 나타낸 그래프입니다.
그렇다면 여기서 확실한 선수가 누가 있을까요

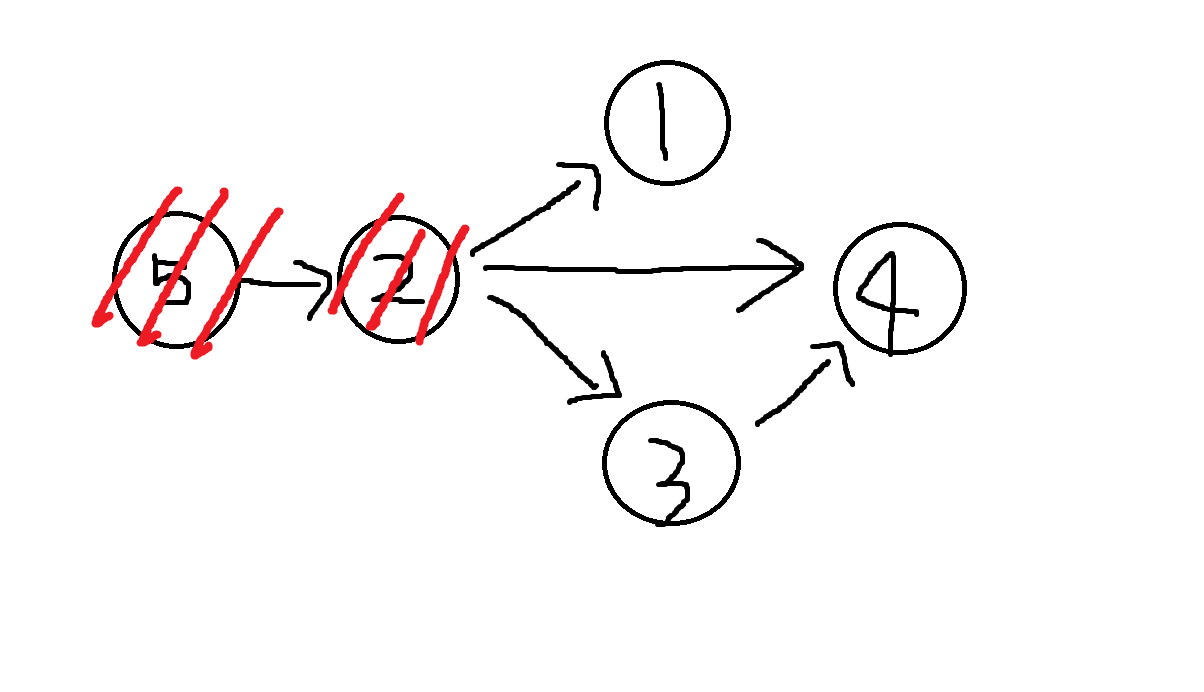
2번은 5번을 이기고 1,3,4번에게 졌으므로 확실한 4위가 되었고, 이러한 2번에게 진 5번은 자연스럽게 5등이 되게됩니다. 그럼 총 2명의 선수가 정확하겠네요.

나머지는 어떨까요?
4번은 1등일까요? 아닙니다. 4번은 2,3번을 이겼습니다. (*5번은 2번에게 졌으므로 자연스럽게 이긴걸로 카운팅됩니다.) 다만, 1번과는 경기를 해본적이 없을 뿐더러 1번과 2번은 경기를 했지만, 1번과 3번은 경기를 안했기에 1번과 3번, 4번의 등수는 모호해집니다.

여기서 알 수 있는 점은 5번과 2번 선수는 DFS로 타고 들어가면 모든 노드를 방문했다는 점입니다.
저는 이 점을 활용했습니다.

이긴 선수 중심의 그래프와 진 선수 중심의 그래프를 2차원 벡터를 활용하여 나타내보면 다음과 같습니다.

//누구를 이겼는지 단방향 그래프 형식으로 정리
    vector<vector<int>> win;
    for (int i = 0; i <= n; i++) {
        vector<int> temp;
        win.push_back(temp);
    }
    for (int i = 0; i < results.size(); i++) {
        win[results[i][0]].push_back(results[i][1]);
    }

    //누구에게 졌는지 단방향 그래프 형식으로 정리
    vector<vector<int>> lose;
    for (int i = 0; i <= n; i++) {
        vector<int> temp;
        lose.push_back(temp);
    }
    for (int i = 0; i < results.size(); i++) {
        lose[results[i][1]].push_back(results[i][0]);
    }

이긴 선수 중심

1 | 2
2 | 5
3 | 2
4 | 2 3
5 |

진 선수 중심

1 |
2 | 1,3,4
3 | 4
4 |
5 | 2

이긴 선수 중심 2차원 벡터로 DFS를 사용하게 된다면 이긴 노드를 방문할 것이고,
진 선수 중심 2차원 벡터로 DFS를 사용하게 된다면 진 노드를 방문할 것입니다!

void DFS(int start, vector<vector<int>> gameWinLose) {
    for (int i = 0; i < gameWinLose[start].size(); i++) {
        if (!isVisited[gameWinLose[start][i]]) {
            isVisited[gameWinLose[start][i]] = true;
            DFS(gameWinLose[start][i], gameWinLose);
        }
    }
    return;
}

이렇게 두 개의 조건으로 DFS를 돌린 후에 자신을 제외한 모든 노드를 방문한다면 DFS를 시작한 선수는 순위를 정확히 알 수 있습니다.

		DFS(i, win);
        DFS(i, lose);
        for (int j = 1; j <= n; j++) {
            if (!isVisited[j]) {
                isCheck = false;
                break;
            }
        }
        if (isCheck)
            answer++;

예시를 먼저 실행해볼까요?

1번부터 실행해보겠습니다.

이긴 것 실행

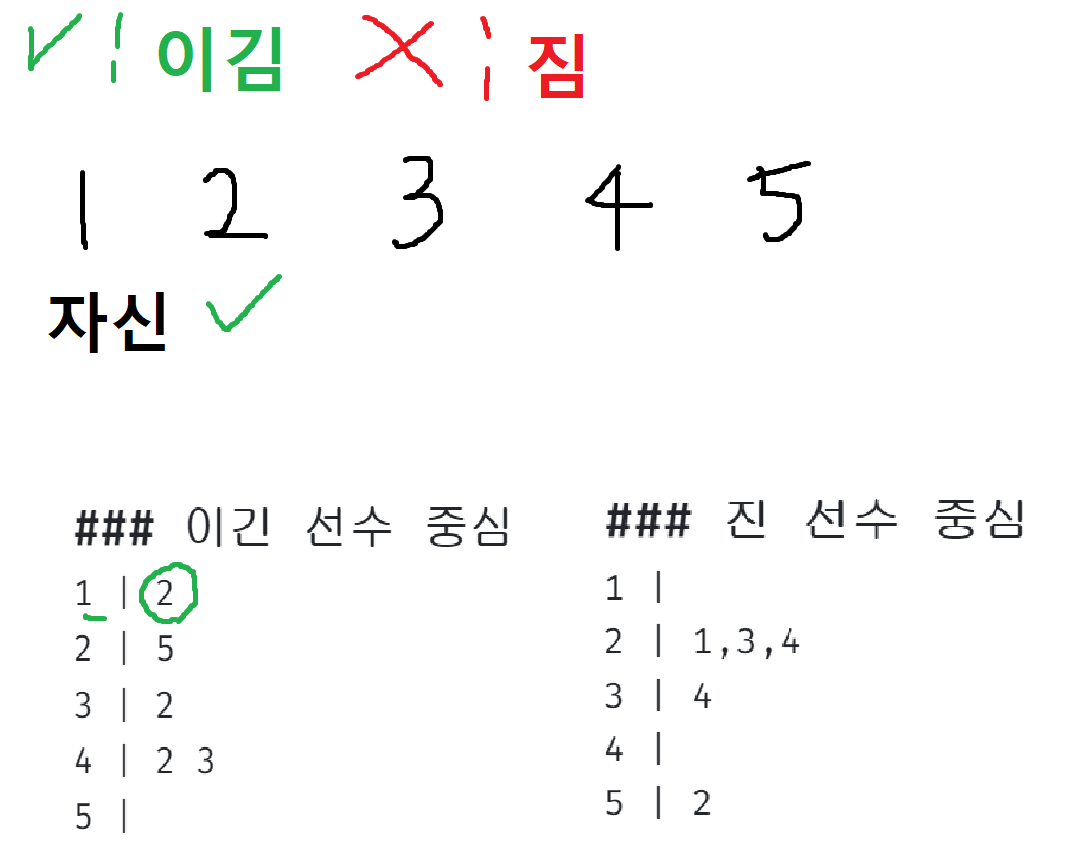
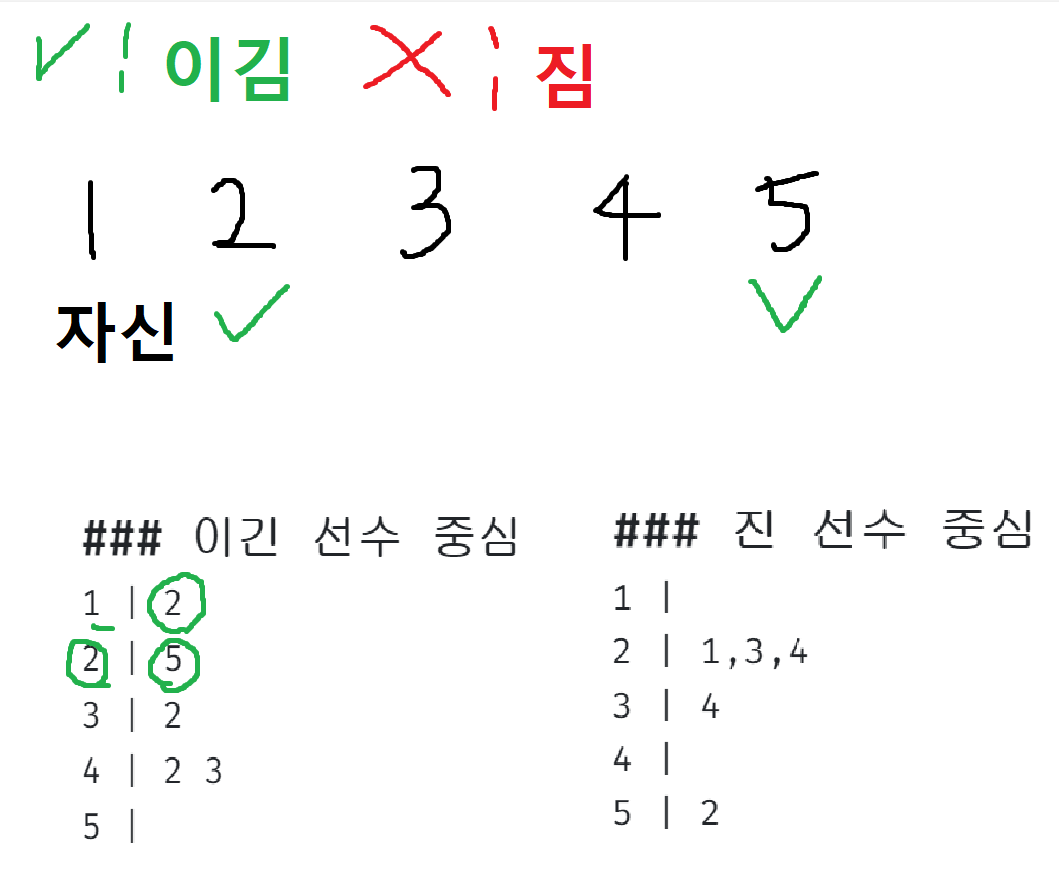
진 것 실행

이렇게 보았을 때 1번은 모든 노드를 방문하지 않았으므로 순위가 모호해집니다.

다음 2번선수까지 실행 해보겠습니다.

이긴 것 실행

진 것 실행

이렇게 2번 선수는 모든 노드를 방문했으므로 순위를 정확히 알 수 있습니다.

최종 코드

#include<iostream>
#include<vector>

using namespace std;

//방문 처리할 전역변수
bool isVisited[102];

void DFS(int start, vector<vector<int>> gameWinLose) {
    for (int i = 0; i < gameWinLose[start].size(); i++) {
        if (!isVisited[gameWinLose[start][i]]) {
            isVisited[gameWinLose[start][i]] = true;
            DFS(gameWinLose[start][i], gameWinLose);
        }
    }
    return;
}
int solution(int n, vector<vector<int>> results) {
    int answer = 0;

    //누구를 이겼는지 단방향 그래프 형식으로 정리
    vector<vector<int>> win;
    for (int i = 0; i <= n; i++) {
        vector<int> temp;
        win.push_back(temp);
    }
    for (int i = 0; i < results.size(); i++) {
        win[results[i][0]].push_back(results[i][1]);
    }

    //누구에게 졌는지 단방향 그래프 형식으로 정리
    vector<vector<int>> lose;
    for (int i = 0; i <= n; i++) {
        vector<int> temp;
        lose.push_back(temp);
    }
    for (int i = 0; i < results.size(); i++) {
        lose[results[i][1]].push_back(results[i][0]);
    }

    //각 노드에서 시작하여 이긴 노드와 진 노드를 DFS형식으로 탐색하여 
    //모든 노드를 방문했다면 이기거나 진 사람이 모두 있다는 것
    //하나라도 방문처리가 안되어있다면 누군가와는 연결되어있지 않아 그 노드와의 순위여부는 알 수 없다.
    for (int i = 1; i <= n; i++) {
        bool isCheck = true;
        //방문 처리 초기화
        fill(&isVisited[1], &isVisited[n + 1], false);
        isVisited[i] = true;
        DFS(i, win);
        DFS(i, lose);
        for (int j = 1; j <= n; j++) {
            if (!isVisited[j]) {
                isCheck = false;
                break;
            }
        }
        if (isCheck)
            answer++;
    }
    return answer;
}