문제 설명
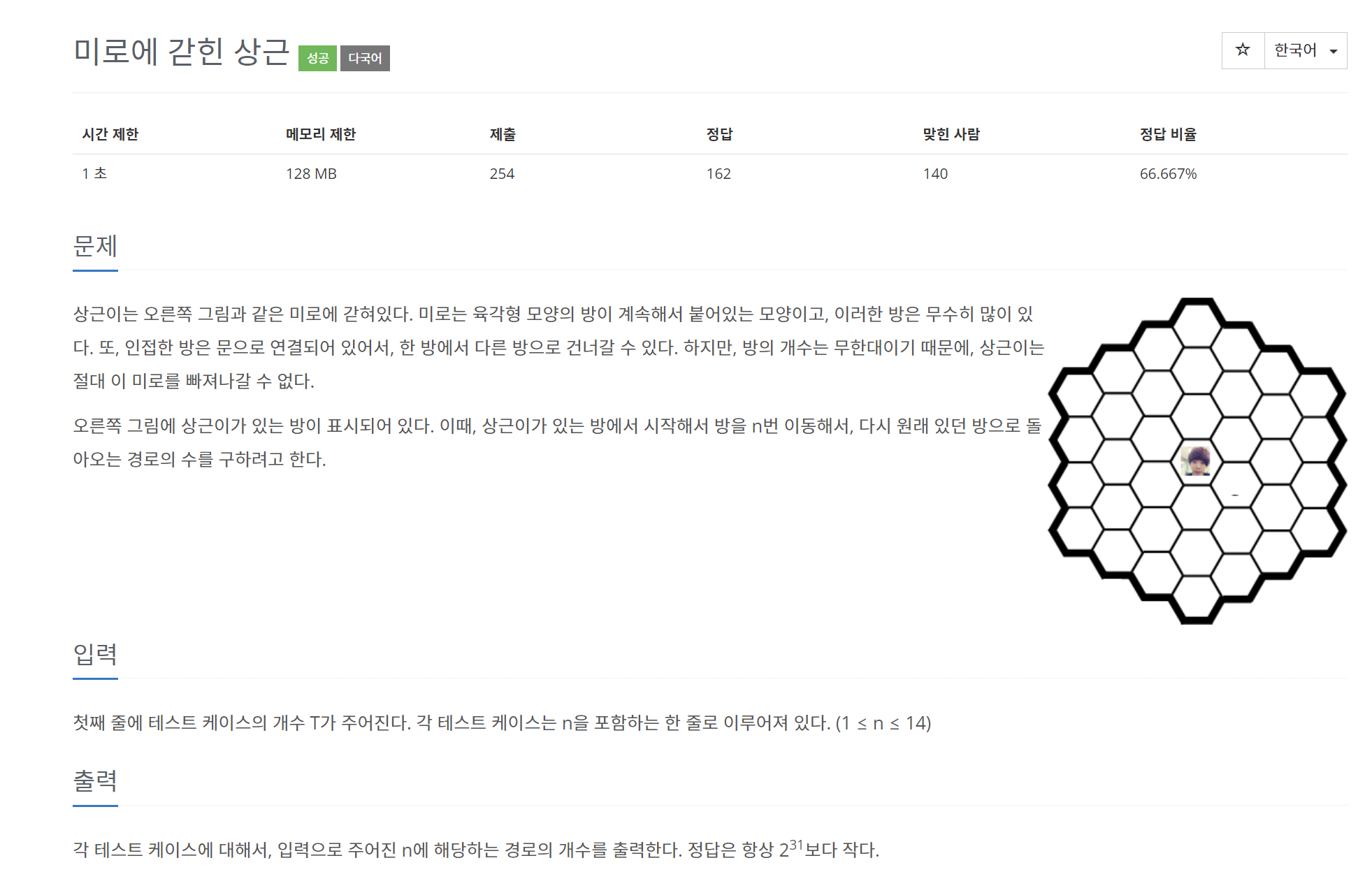
이번 문제는 DP를 활용하여 풀 수 있습니다.
먼저 해당 미로의 정보를 다음과 같이 담아줍니다.
상근이가 있는 위치는 정중앙으로 설명하기 쉽도록 S로 표현하겠습니다.
---0-0-0-0---
--0-0-0-0-0--
-0-0-0-0-0-0-
0-0-0-S-0-0-0
-0-0-0-0-0-0-
--0-0-0-0-0--
---0-0-0-0---
n번의 이동 후 자기 자신의 방으로 돌아왔을 경우, 최대로 이동할 수 있는 거리는 어느정도일까 생각해보면 n/2만큼 한 방향으로 쭉 나아가는 경우가 최대로 멀리 이동할 수 있는 경우입니다.
우리는 이를 통해 횟수에 따른 최대 육각형의 한 변의 길이를 예측하여 계산할 수 있습니다.
---0-0-0-0---
--0-0-0-0-0--
-0-0-0-0-0-0-
0-0-0-S-0-0-0 --> 배열의 최대 크기 = 13개
-0-0-0-0-0-0-
--0-0-0-0-0--
---0-0-0-0---
Ex) 위의 경우 중앙으로부터 최대 6번으로 멀리 나갔다 돌아올 수 있습니다.
+ 추가로 한 변은 (6 / 2 + 1)인 것을 알 수 있으며,
+ 한 줄에 필요한 최대 배열의 크기는 (6 X 2 + 1)인 것을 알 수 있습니다.
그렇다면 저 위의 경우를 봐서 그림을 그리기 위한 규칙을 찾아봅시다.
크게 보면 위의 그림은 한 변의 길이가 4인 육각형입니다. 중앙으로부터 3만큼 뻗어있죠.
그렇다면, 맨 윗줄부터 줄을 천천히 봐봅시다.
1번째 줄은
- 양 옆으로 '-'이 연속으로 3개가 나오며
- '0'이 나온 시점에는 한변의 길이인 4개가 나오며
- 4개 사이에는 '-'이 4 - 1개가 들어있는 것을 볼 수 있습니다.
2번째 줄은
- 양 옆으로 '-'이 연속으로 3-1개가 나오며
- '0'이 나온 시점에는 4 + 1개가 나오며
- 4 + 1개 사이에는 '-'이 4 + 1 - 1개가 들어있는 것을 볼 수 있습니다.
대충 규칙이 보이시죠?
중앙으로부터 아래쪽은 반대로 해주면 되는 것을 볼 수 있습니다.
입력 조건을 보면 n은 14이하까지 나타나져있습니다.
이를 통해 우리는 무한히 있는 육각형의 방이 아닌 14번 으로 왔다가 올 수 있는 최대 방의 거리를 확인해보면 한 변이 (14 / 2 + 1 = ) 8인 것을 알 수 있고, 한줄의 배열의 최대 크기는 (14 X 2 + 1 = ) 29인 것을 알 수 있습니다.
또한, 이를 통해 최대 미로를 미리 그려볼 수 있습니다.//미로 그리기 for (int i = 0; i < centerY; i++) { for (int j = 0; j < 29; j++) { if (j < MAX / 2 - i || j > 29 - (MAX / 2 - i) || ((i + 1) % 2 == 1 && (j + 1) % 2 == 1) || ((i + 1) % 2 == 0 && (j + 1) % 2 == 0)) miro[i][j] = '-'; else miro[i][j] = '0'; } } for (int i = centerY; i <= MAX; i++) { for (int j = 0; j < 29; j++) { if (j < (MAX / 2 - (MAX / 2 - (i - centerY))) || j > 29 - (MAX / 2 - (MAX / 2 - (i - centerY))) || ((i + 1) % 2 == 1 && (j + 1) % 2 == 1) || ((i + 1) % 2 == 0 && (j + 1) % 2 == 0)) miro[i][j] = '-'; else miro[i][j] = '0'; } }
미로를 그려보기만 해도 피곤하네요..
하지만, 이제 모든 것이 끝났습니다.
DP를 활용하여 상근이의 위치에서 출발하여, 상근이의 위치에 n번만에 도착했을 경우를 배열에 저장해주겠습니다.
#define MAX 14 //미로 틀 char miro[MAX + 1][29]; //int dp[7 * 2 + 1][(7 * 2)+8+7]; //1~14번만에 특정 위치에 도달할 경우의 수 int dp[MAX + 1][MAX + 1][29];이렇게 dp의 배열을 정의해주고,
이제 dp를 돌려보겠습니다.
먼저 시작점을 주어줘야겠죠?
최대 배열의 크기를 정의해줬으니 상근이의 위치는 그 가운데이니 좌표값을 예측해볼 수 있습니다.int centerY = 7; int centerX = 14; //경로 탐색 DPSetting(centerY, centerX);
DPSetting 함수를 살펴 보겠습니다.
방향은 6방향인데, 대각선과 자기 위치에서 좌, 우로 2씩 +-한 부분이 방향입니다.
위의 예시 배열을 보시면 이해가 편하실 것 같습니다.queue를 활용하여, 정보를 담아주고, pair를 활용하여 자신이 있는 위치와 depth를 넣을 수 있도록 해줍니다.
초기값은 시작 위치에서 0의 depth로 시작하겠습니다.
6방향으로 뻗어나가서면서, n번째에 해당 위치에 도착한 적이 없으면 해당 위치를 queue를 넣어주면서 계산해줍니다.
//방향 int xSign[6] = { -1, -1, 1, 1, 2, -2 }; int ySign[6] = { 1, -1, 1, -1, 0, 0 }; //방문처리 bool isVisited[MAX + 1][MAX + 1][29]; void DPSetting(int startY, int startX) { //현재 위치 좌표, depth값 queue<pair<pair<int, int>, int>> searchQue; searchQue.push({ { startY,startX }, 0 }); //0번만에 (startX, startY)에 도착할 경우의 수 dp[0][startY][startX] = 1; while (!searchQue.empty()) { int y = searchQue.front().first.first; int x = searchQue.front().first.second; int curDepth = searchQue.front().second; searchQue.pop(); //depth가 14를 벗어나면, n의 입력제한에 위반되므로 제외해줍니다. if (curDepth + 1 > MAX) continue; //6방향으로 뻗어나가며 자신의 depth + 1을 더해준다. for (int i = 0; i < 6; i++) { int nextY = y + ySign[i]; int nextX = x + xSign[i]; //현재 최대치를 벗어나면 -> 고려할 필요 없는 부분 if (nextY < 0 || nextY > MAX || nextX < 0 || nextX > 28) continue; // 계산 상 나올 확률은 없다 판단하지만, 방어 코드로 넣어줬습니다. if (miro[nextY][nextX] == '-') continue; //curDepth + 1번째에 (nextX, nextY)에 도착할 경우의 수에 dp[curDepth][y]의 경우의 수를 더해줍니다. dp[curDepth + 1][nextY][nextX] += dp[curDepth][y][x]; //curDepth + 1번째에 (nextX, nextY)에 도착한 적이 없다면, queue에 넣어준다. if (!isVisited[curDepth + 1][nextY][nextX]) { searchQue.push({ {nextY, nextX},curDepth + 1 }); isVisited[curDepth + 1][nextY][nextX] = true; } } } }
이것을 이제 사용해보겠습니다.
사실 사용 자체는 간단합니다.
case를 받으면 해당 횟수에 (centerX, centerY), 즉 상근이의 위치에 도달할 경우의 수를 출력해주기만 하면 됩니다.
왜냐하면, DPSetting(centerY, centerX);를 호출한 순간부터 이미 경로들의 경우의 수가 계산되었기 때문이죠.
for (int t = 0; t < tc; t++) { int maxCnt; cin >> maxCnt; cout << dp[maxCnt][centerY][centerX] << "\n"; }

최종 코드(.cpp)
#include<iostream>
#include<queue>
using namespace std;
void init() {
ios_base::sync_with_stdio(false);
cin.tie(0);
std::cout.tie(0);
}
#define MAX 14
//미로 틀
char miro[MAX + 1][29];
//int dp[7 * 2 + 1][(7 * 2)+8+7];
//1~14번만에 특정 위치에 도달할 경우의 수
int dp[MAX + 1][MAX + 1][29];
//방향
int xSign[6] = { -1, -1, 1, 1, 2, -2 };
int ySign[6] = { 1, -1, 1, -1, 0, 0 };
//방문처리
bool isVisited[MAX + 1][MAX + 1][29];
void DPSetting(int startY, int startX) {
queue<pair<pair<int, int>, int>> searchQue;
searchQue.push({ { startY,startX }, 0 });
dp[0][startY][startX] = 1;
while (!searchQue.empty()) {
int y = searchQue.front().first.first;
int x = searchQue.front().first.second;
int curDepth = searchQue.front().second;
searchQue.pop();
if (curDepth + 1 > MAX)
continue;
//6방향으로 뻗어나가며 자신의 depth + 1을 더해준다.
for (int i = 0; i < 6; i++) {
int nextY = y + ySign[i];
int nextX = x + xSign[i];
if (nextY < 0 || nextY > MAX || nextX < 0 || nextX > 28)
continue;
if (miro[nextY][nextX] == '-')
continue;
dp[curDepth + 1][nextY][nextX] += dp[curDepth][y][x];
if (!isVisited[curDepth + 1][nextY][nextX]) {
searchQue.push({ {nextY, nextX},curDepth + 1 });
isVisited[curDepth + 1][nextY][nextX] = true;
}
}
}
}
int main() {
init();
int centerY = 7;
int centerX = 14;
int tc;
cin >> tc;
//미로 그리기
for (int i = 0; i < centerY; i++) {
for (int j = 0; j < 29; j++) {
if (j < MAX / 2 - i || j > 29 - (MAX / 2 - i)
|| ((i + 1) % 2 == 1 && (j + 1) % 2 == 1)
|| ((i + 1) % 2 == 0 && (j + 1) % 2 == 0))
miro[i][j] = '-';
else
miro[i][j] = '0';
}
}
for (int i = centerY; i <= MAX; i++) {
for (int j = 0; j < 29; j++) {
if (j < (MAX / 2 - (MAX / 2 - (i - centerY))) || j > 29 - (MAX / 2 - (MAX / 2 - (i - centerY)))
|| ((i + 1) % 2 == 1 && (j + 1) % 2 == 1)
|| ((i + 1) % 2 == 0 && (j + 1) % 2 == 0))
miro[i][j] = '-';
else
miro[i][j] = '0';
}
}
//경로 탐색
DPSetting(centerY, centerX);
for (int t = 0; t < tc; t++) {
int maxCnt;
cin >> maxCnt;
cout << dp[maxCnt][centerY][centerX] << "\n";
}
}
