정렬

Bubble sort

개념

• 비교 기반 정렬 알고리즘.
• 두개의 요소를 반복적으로 비교해가며 왼쪽이 오른쪽보다 클 경우 위치를 바꾼다.
• 시간복잡도는 O(N^2)이므로 대규모 데이터 세트에는 적합하지 않다.
• 첫번쨰와 두번째 비교, 두번째와 세번째 비교, 세번째와 네번쨰 비교.. 반복...

원리

• 배열의 처음 시작부분부터 시작해 근접한 두개의 요소를 한쌍으로(첫번째와 두번째) 크기비교를 반복한다, 만약 왼쪽이 오른쪽보다 크다면 위치를 바꾼다.
• 만약 위의 상황이 만족되서 위치를 바꿨다면 다음 두개를 비교하며 반복(두번째와 세번째).
• 1회전이 끝날때마다 배열의 제일 큰 값이 맨 뒤로 간다.
  • 그 다음 1회전이 끝나면 2번째로 큰 값이 맨 뒤에서 2번째, 계속 반복.

코드

def bubble_sort(list):
    for i in range(len(list)):
        for j in range(len(list)-1-i):
            if list[j] > list[j+1]:
                # Swap
                our_list[j], list[j+1] = list[j+1], list[j]

Insertion sort

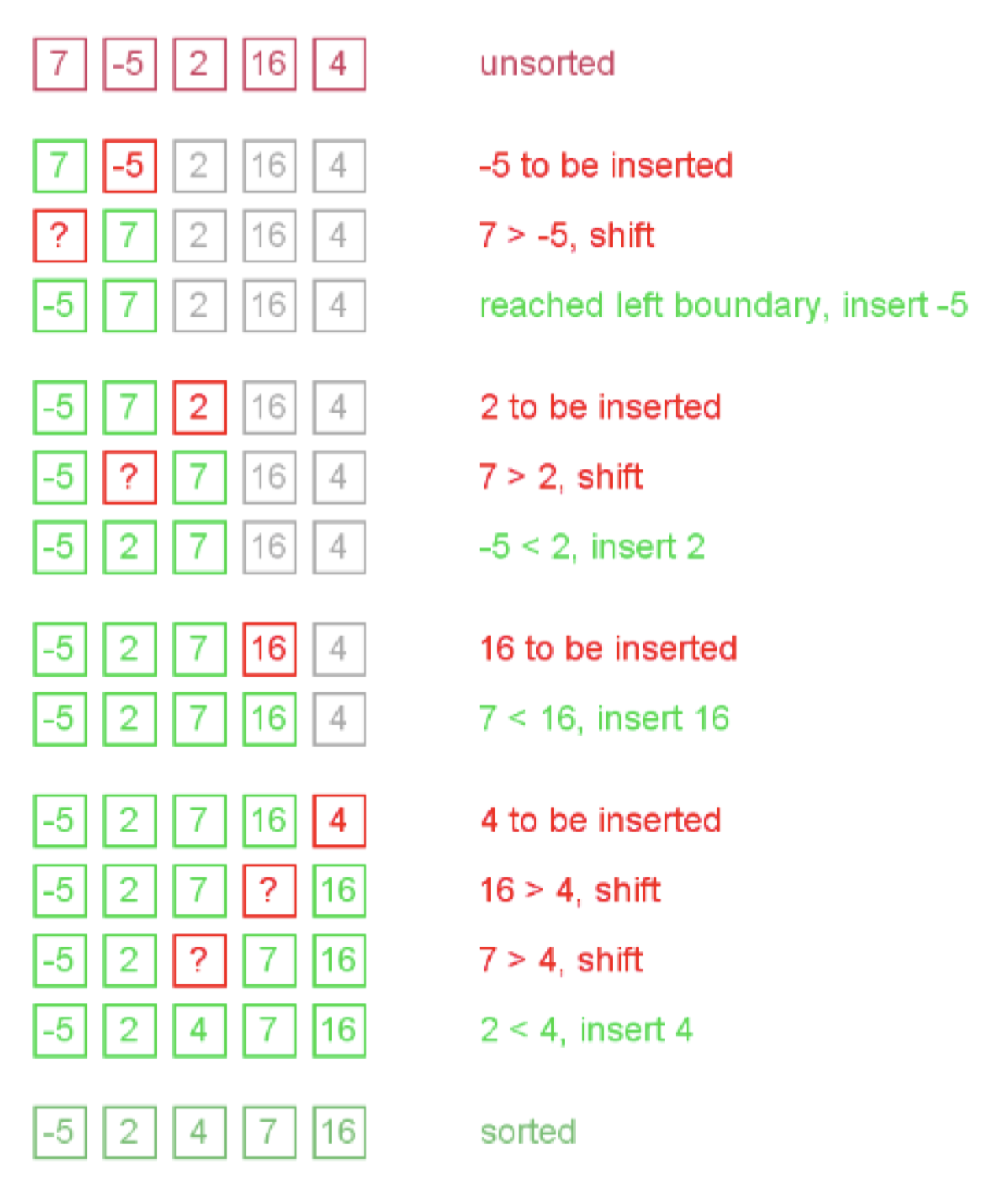
개념

• 시간 복잡도는 O(N^2).
• 배열의 순서대로 요소들을 뽑아가며 배열의 왼쪽 부분에 정렬하며 넣는 방식.
  • 정렬하며 넣기 때문에 반복수가 거듭될수록 탐색범위가 늘어난다.

원리

• 정렬의 시작은 배열의 두번쨰 요소부터 순서대로 다음칸으로 이동하며 정렬한다.
• 현재 정렬을 하고 있는 배열의 n번째 요소에서 n-1, n-2 점차 줄여나가며 n번째 요소와 크기비교를 한다.
  • 만약 n번째가 n-k번째보다 클경우 n-k+1번째에 n-k+1를 포함한 이후 요소들을 전부 오른쪽으로 한칸씩 옮긴후 n번째값을 n-k+1번째 자리에 넣는다.
  • 반복.

코드

def insertionSort(array):
    for index in range(1, len(array)):
        cursor = array[index]
        j = index-1
        # reverse traverse here.
        while j>=0 and array[j]>cursor:
            array[j+1] = array[j]
            j = j-1
        array[j+1] = cursor

Merge sort

개념

• 분할정복(divide and conquer)
  • 작은 수준의 문제로 나눈 후 각각을 해결한 후 결과를 합쳐가며 최종 문제를 해결하는 방식.
• 정렬해야할 배열의 길이가 같다면 내용과 관계없이 정렬되는 시간은 동일.
• 시간 복잡도는 O(N*log N).

원리

• 재귀함수를 이용하여 구현.
  • 배열을 하나의 요소가 될때까지 계속 자른다.
  • 다시 나눠진 배열을 작은 순서부터 합친다.
  • 반복.

코드

def mergeSort(myList):
    if len(myList)>1:
        mid = len(myList) // 2
        left = myList[:mid]
        right = myList[mid:]

        # Recursive call on each half
        mergeSort(left)
        mergeSort(right)

        # Two iterators for traversing the two halves
        i = 0
        j = 0
        
        # Iterator for the main list
        k = 0
        
        while i<len(left) and j<len(right):
            if left[i]<=right[j]:
              # The value from the left half has been used
              myList[k] = left[i]
              # Move the iterator forward
              i += 1
            else:
                myList[k] = right[j]
                j += 1
            # Move to the next slot
            k += 1

        # For all the remaining values
        while i<len(left):
            myList[k] = left[i]
            i += 1
            k += 1

        while j<len(right):
            myList[k]=right[j]
            j += 1
            k += 1