BCNF (Boyce-Codd Normal Form)
- 저번에 여기에서 1NF~3NF까지 알아봤다.
- BCNF의 조건은 제3 정규형의 조건을 만족해야 하며, 추가로 다음과 같다.
- X -> Y인 모든 X,Y에 대하여
- Y가 X의 부분집합이거나
ABC->A- X는 후보키어야 한다.
- 아래 사진이 반례.
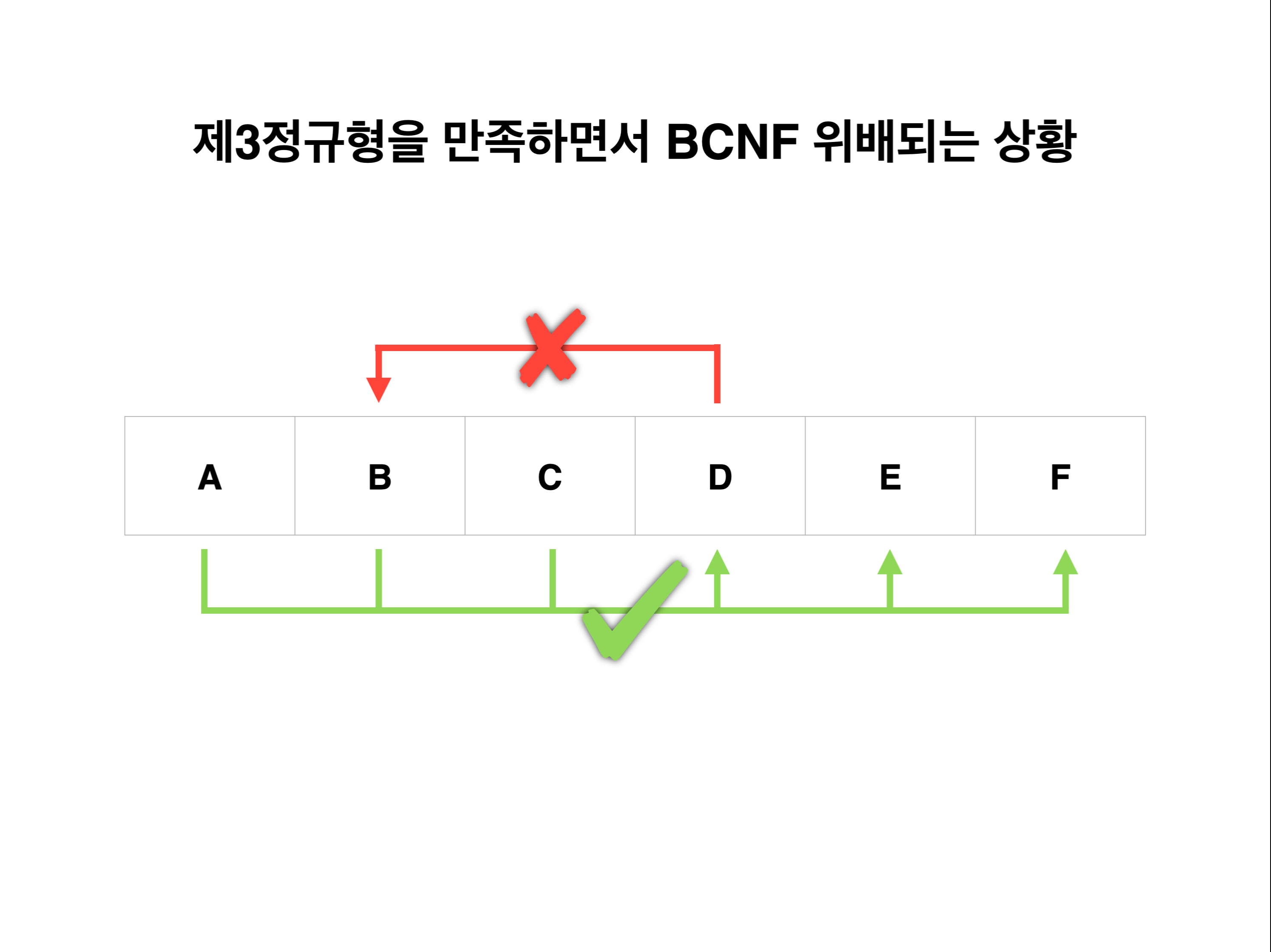
- 위 사진이 두번째 조건
X는 후보키어야 한다를 위배하는 상황이다.- 위 사진에서 키는 A,B,C 세가지만 존재하며 D는 결정자에 의해 정해지는 값이다.
- 이때, D에 의해 B가 결정되는 관계가 성립된다면 BCNF를 만족할 수 없다.
- 이런 경우엔 아래처럼 테이블을 분리해 준다고 한다.
| A | C | D | E | F |
|---|
| D | B |
|---|
A,C->D,E,FD->B- 이렇게 바꿔주면 BCNF의 조건중 하나인
X는 후보키어야 한다를 만족시키게된다.- BCNF는 좀더 강한 제3정규형 이란 느낌이 든다.
1NF ~ BCNF 요약
- 1NF: PK, 원자성
- 2NF: 부분 함수적 종속 X -> 완전 함수적 종속
- 3NF: 이행 함수적 종속 X
- BCNF: 모든 결정자는 후보키이다.
