01. 병합정렬 개념
1) 병합정렬의 작동순서
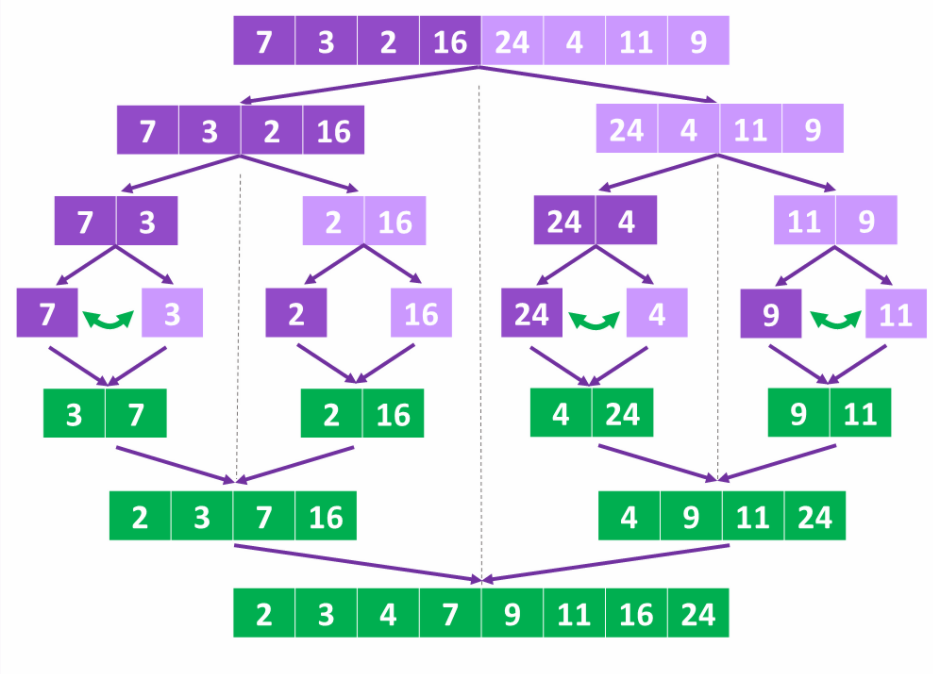
1) 분할(divide): 원소가 1개인 부분 리스트가 될 때까지 리스트를 반으로 쪼갠다.
2) 정복 & 결합(conquer & combine): 각 부분 리스트 쌍을 재귀적으로 정렬하며 하나의 정렬된 리스트로 합병한다. 즉, 정렬과 합병을 동시에 한다.
3) 하나의 정렬된 리스트 남는다.
02. 병합정렬 코드(Python)
1) python 코드
# 2. L, R 부분 리스트를 정렬하며 병합하기(Conquer & Combine)
def merge(L, R):
# 2-1. L과 R의 0번째 인덱스부터 보면서 서로 비교해서 오름차순으로 merge_list에 집어 넣기
merge_list = []
L_indx = 0
R_indx = 0
# L이나 R 둘 중 하나가 전부 사용될 때까지 반복한다.
while L_indx < len(L) and R_indx < len(R):
if L[L_indx] >= R[R_indx]:
merge_list.append(R[R_indx])
R_indx += 1
else:
merge_list.append(L[L_indx])
L_indx += 1
# 2-2. L이나 R 둘 중 하나가 전부 사용되고 남은 것들을 집어 넣기
if L_indx < len(L):
merge_list += L[L_indx:]
elif R_indx < len(R):
merge_list += R[R_indx:]
return merge_list
# 1. 분할하기(divide)
def partition(data):
N = len(data)
# 1-2. 종료조건 -> 더 이상 쪼갤 것이 없을 때
if N <= 1:
return data
# 1-1. 진행
L = partition(data[:N//2])
R = partition(data[N//2:])
# L과 R이 지정되면 merge하면서 조각을 정렬한다.
return merge(L, R) # merge한 결과는 아래의 재귀 스택으로 들어간다.
numbers = [0, 55, 22, 33, 2, 1, 10, 26, 42]
print(numbers) # 정렬 전 [0, 55, 22, 33, 2, 1, 10, 26, 42]
print(partition(numbers)) # 정렬 후 [0, 1, 2, 10, 22, 26, 33, 42, 55]2) 재귀함수 디버깅
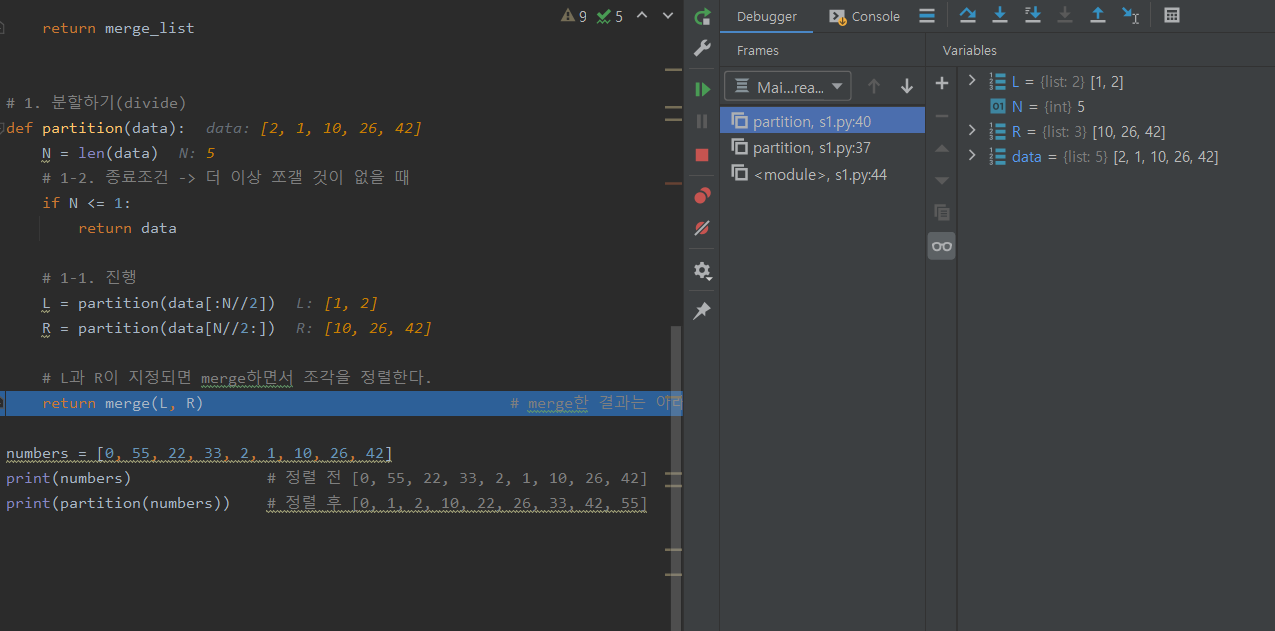
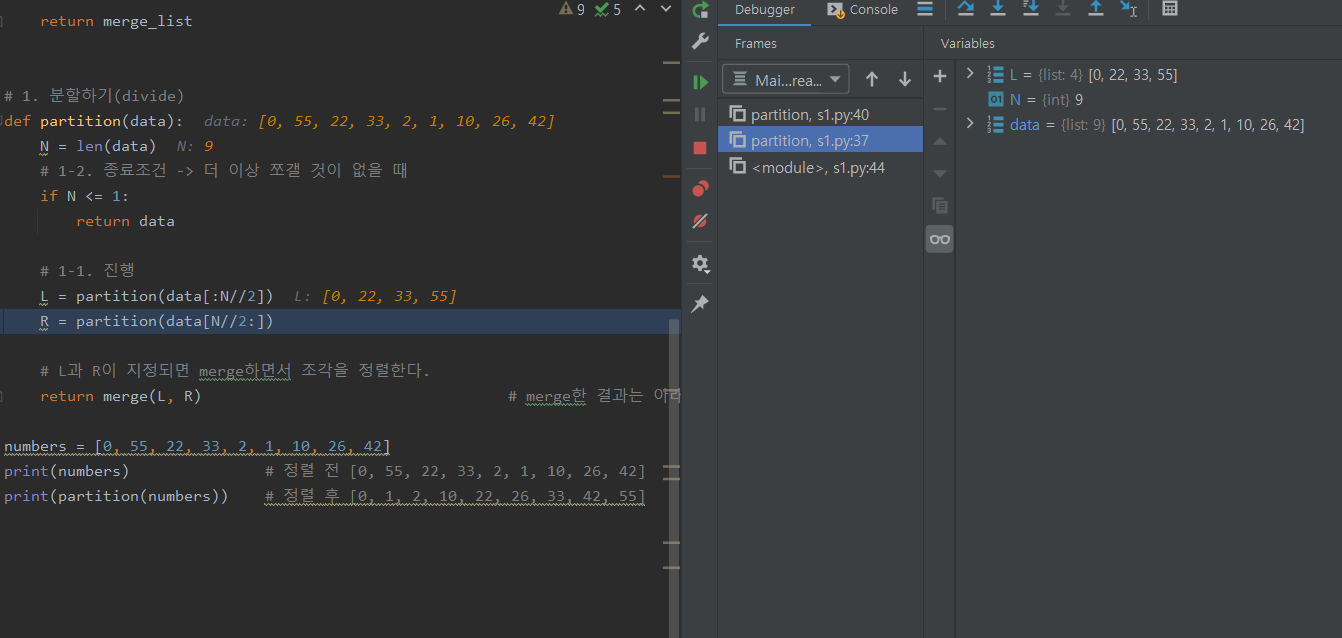
- 첫번째 사진에 있는 재귀 함수에서 정렬된 [1, 2, 10, 26, 42]는 아래 사진에 있는 재귀함수의 R로 지정되어 L과 정렬되며 합병된다.
❗ partition 과정에서 merge sort된 L과 R을 호출하여 다시 merge sort한다.
03. 병합정렬 시간복잡도 : O(nlogn)
1) 계산 과정
-
T(n) : n개의 원소를 가지고 있는 배열을 merge sort로 정렬했을 때의 시간 복잡도
-
T(1) = 1 : 1개의 원소를 정렬하는 시간
- T(n) = 2*T(n/2) + n-1
- 2*T(n/2) : 두 개의 부분 리스트로 쪼개고, 각 부분 리스트를 merge sort
- n - 1 : 부분 리스트의 합병 과정에서 부분 리스트의 원소를 반대편 리스트의 원소와 각각 비교
- n = 2^k라고 했을 때, T(n) = O(nlogn)
04. 병합정렬 특징
- 분할 정복(divide and conquer) 알고리즘의 하나
- 분할 정복이란 문제를 작은 2개의 문제로 분리하고, 각각을 해결한 다음, 그 결과를 모아서 원래의 문제를 해결하는 전략
- 정렬의 과정에서 추가적인 임시 리스트가 필요해, 메모리를 많이 사용한다.
- 최선의 시간복잡도와 최악의 시간 복잡도가 O(nlogn)으로 동일하다. 즉, 입력 데이터에 영향을 받지 않는다.